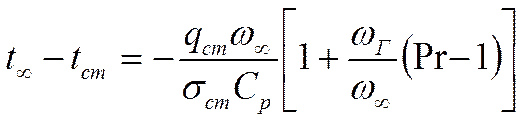
Где: 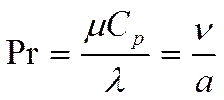
![]() по определению:
по определению: 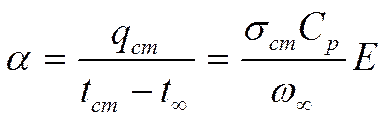 (*)
(*)
Где: 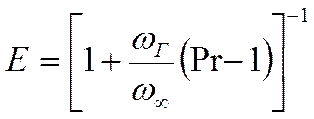
Заменим 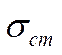 в выражении (*) на коэффициент трения
в выражении (*) на коэффициент трения 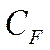 :
:
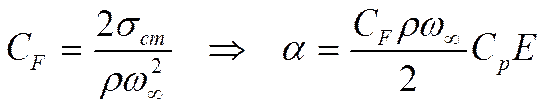 (**)
(**)
Введём определение: безразмерный комплекс
равный 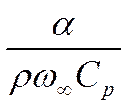 называется критерием
Стантона:
называется критерием
Стантона:
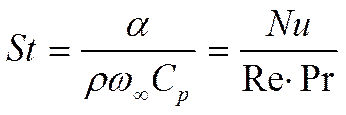
Из (**) получаем:

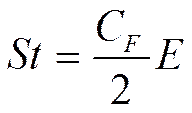
Интенсивность теплообмена напрямую зависит от трения на стенке.
Рассмотрим ситуацию, когда ![]() :
:

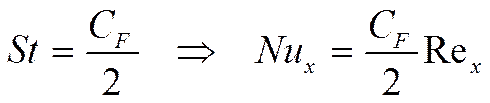 (***)
(***)
Для ламинарного режима мы имели:
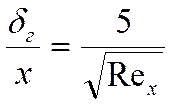
Для
турбулентного режима экспериментально была найдена связь ![]() :
:
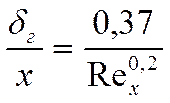
Если мы перейдём к коэффициенту трения, то получим
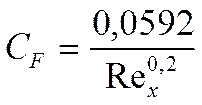 подставим в (***).
подставим в (***).
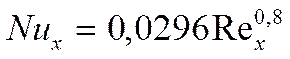
 Если
Если
![]() :
:
![]()
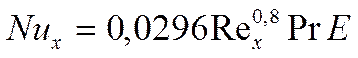
опытные данные.
Расчёт интенсивности теплообмена при вынужденном стабилизированном течении жидкости в трубе.
Особенности движения жидкости на начальном участке.
![]() На входе в любой канал в
жидкости начинает формироваться пограничный слой:
На входе в любой канал в
жидкости начинает формироваться пограничный слой:

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()


![]()

![]()

![]()
![]()
![]()
![]() (по радиусу трубы)
(по радиусу трубы)
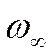 |
|||||
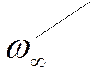 |
|||||
пограничный слой
Задача
симметричная и пограничный слой смыкается. Зона, где ещё формируется профиль
скорости, называется начальным участком (![]() ).
Если речь идёт о формирования профиля скорости, то говорят о начальном участке
как о начальном гидродинамическом участке
).
Если речь идёт о формирования профиля скорости, то говорят о начальном участке
как о начальном гидродинамическом участке ![]() . Если
говорят о формировании профиля температуры, то начальный участок называется
участком тепловой стабилизации
. Если
говорят о формировании профиля температуры, то начальный участок называется
участком тепловой стабилизации 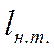 . В общем случае:
. В общем случае: 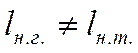 Если длина исследования отнесённая к
диаметру трубы больше L предельного, то течение стабилизированное:
Если длина исследования отнесённая к
диаметру трубы больше L предельного, то течение стабилизированное:
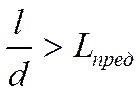
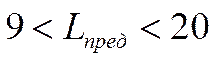
В нашей задаче: 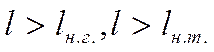 .
.
1) внутренние источники тепла отсутствуют.
2) задача стационарная.
3)
физические параметры жидкости не
зависят от температуры 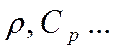
4) Молекулярный перенос тепла в радиальном направлении учитываем, а в осевом не учитываем.
5)
Теплопроводностью в аксиальном
направлении пренебрегаем. Характеристикой теплового потока является ![]() . Пренебрегаем теплопроводностью:
. Пренебрегаем теплопроводностью:
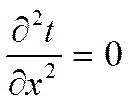
Из-за симметрии задачи:
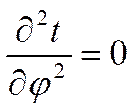
Поток тепла по любому параметру отсутствует.
Важной является теплопроводность в радиальном направлении.
Уравнение энергии:
![]()

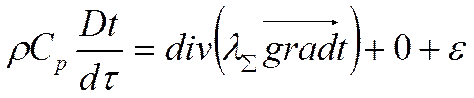
Для характерных тепловых потоков через стенку работой сил вязкого трения можно пренебречь. От субстанциальной производной остаётся:
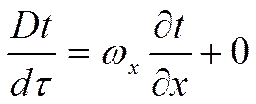
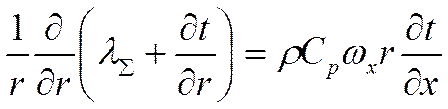
![]() Этого
уравнения не достаточно для решения задачи. Рассмотрим приращение вдоль трубы
на участке
Этого
уравнения не достаточно для решения задачи. Рассмотрим приращение вдоль трубы
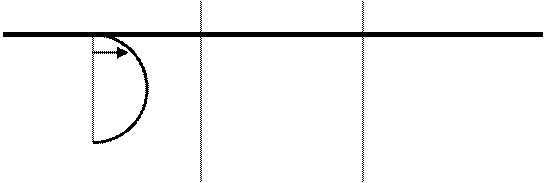
на участке ![]() внешней поверхностью
внешней поверхностью ![]() , поперечным сечением
, поперечным сечением ![]() :
:
 |
![]()
![]()
![]()
![]()
![]()
![]()
Мы имеем профиль скорости и температуры. С учётом профиля можно записать:
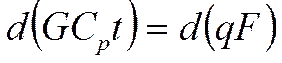
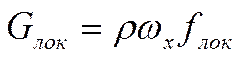 - G на каком-то радиусе.
- G на каком-то радиусе.
Что бы получить полное значение G, надо проинтегрировать:
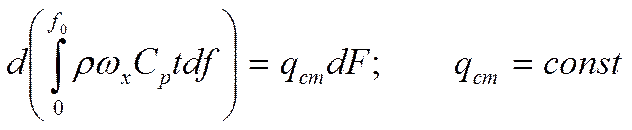
 Рассмотрим
интеграл:
Рассмотрим
интеграл:
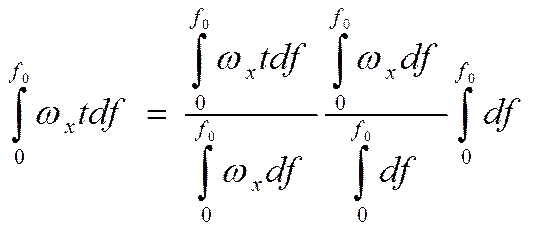
средняя скорость
средневзвешенная температура потока ![]()
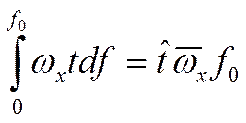
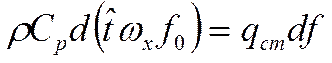
Мы
рассматриваем стабилизированное течение, у которого 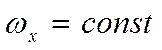
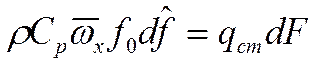
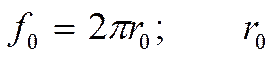 - внутренний радиус трубы.
- внутренний радиус трубы.
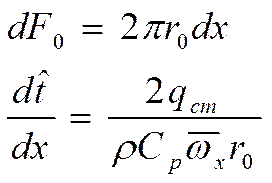
В любой точке потока при сохранении радиуса, приращение температуры одинаково (аналогия с регулярным режимом). Если в профиле температура установилась, то:
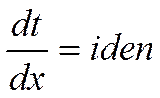 (не зависит от радиуса)
(не зависит от радиуса)
Если бы в одной точке темп охлаждения отличался от другой. то профиль бы менялся. Для стабилизированного потока:
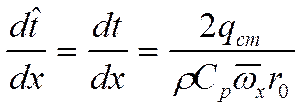
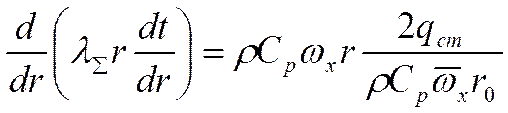 (*)
(*)
Вводим безразмерные величины:
![]()
![]()
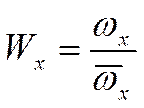 локальная
локальная
средняя по сечению.
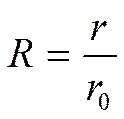
Умножим (*) на ![]() :
:
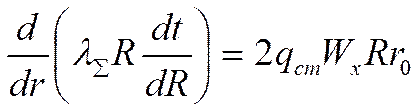
Проинтегрируем:
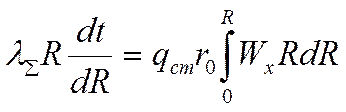
1) Нам потребуется:
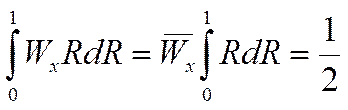 так как
так как 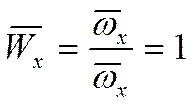
2)
![]() определяет сумму составляющих:
определяет сумму составляющих:
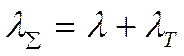
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.