- периметр. известны.
![]()
Предположим, что стержень «тонкий».
Запишем интегральное уравнение баланса в стержне:
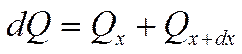 (по направлению тепловых потоков).
(по направлению тепловых потоков).
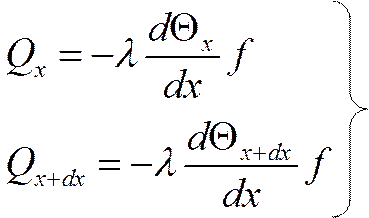 |
по Фурье.
В точке ![]() разложим в ряд Фурье:
разложим в ряд Фурье:
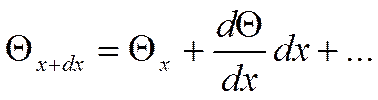
Получаем:
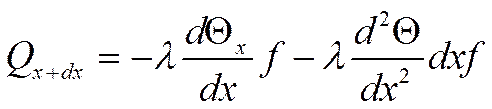
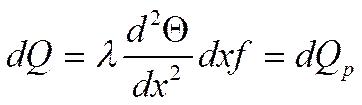
Приращение обусловлено
утечкой через поверхность ![]() .
.
Распишем по Ньютону-Рихману:
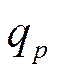
![]()
![]()
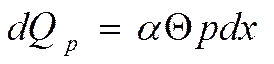
![]() наружная поверхность.
наружная поверхность.
Приравняем:
 |
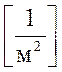
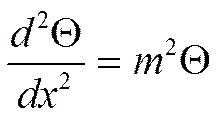 где:
где: 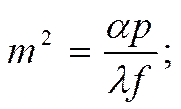
![]() , т.к. величины от которых
, т.к. величины от которых
оно зависит – константы.
Дифференциальное уравнение
теплопроводности в тонком
![]() стержне.
стержне.
Найдём решение этого дифференциального уравнения:
Наше уравнение примет следующий вид:
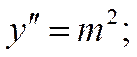
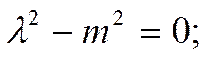
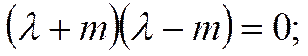
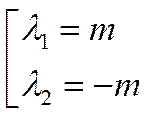
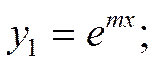
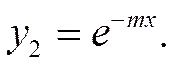
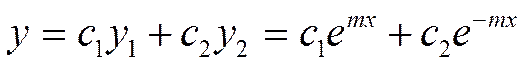
Подставляя ![]() , получаем:
, получаем:
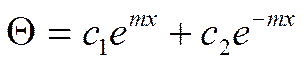 (*)
(*)
Рассмотрим два случая:
1)
Стержень бесконечной длины. ![]()
Граничные условия имеют вид:
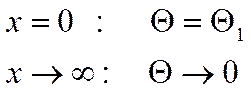
Подставив это в (*), получим:
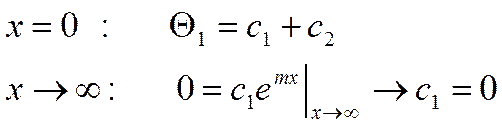
Окончательное решение:
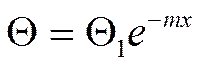
Количество тепла, передаваемого через стенку в окружающую среду:
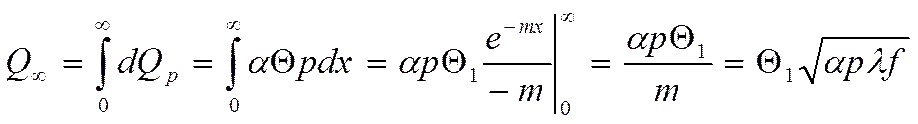
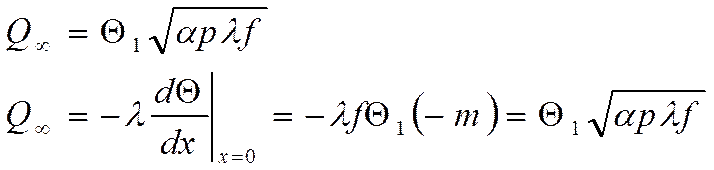
2) Стержень конечной длины.
Граничные условия:
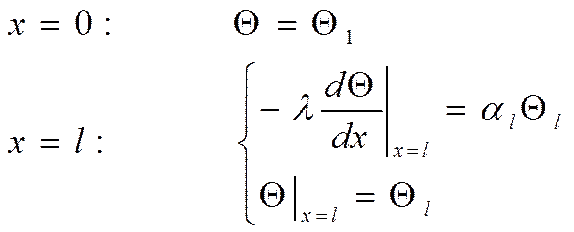 |
(гр. усл. III р.)
Подставим в (*):

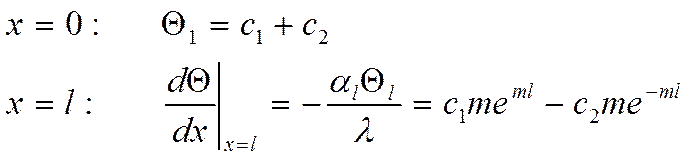
подставим из
решения
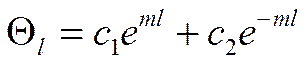
Имеем три неизвестных: ![]() .
.
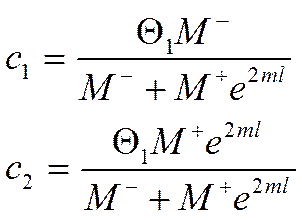
Обозначено:![]() - параметр, который является разностью
между известными значениями
- параметр, который является разностью
между известными значениями ![]()

Произведём вычисления:
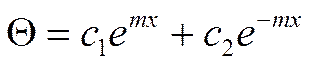 (*)
(*)
Упростим:
![]()
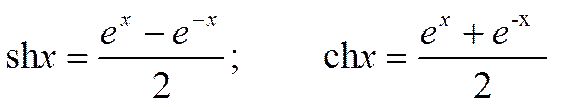 (**)
(**)
Подставим в выражение (*) значения для ![]() и
и ![]() :
:
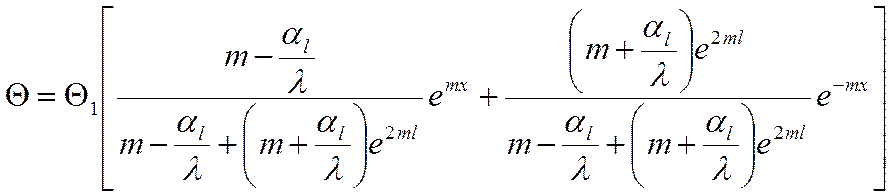
Приведём к общему знаменателю:
![]()
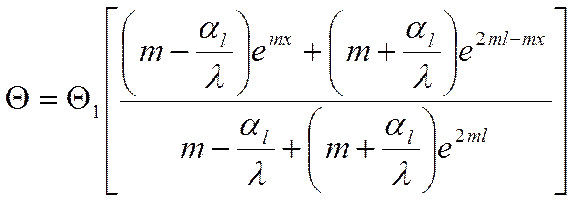
Умножим числитель и
знаменатель на 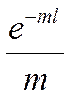 :
:
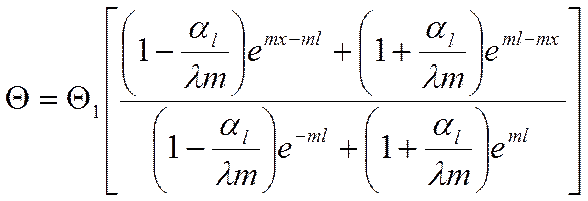
Раскрыв скобки, получим:
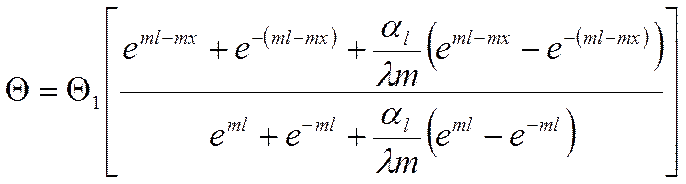
Учитывая (**), окончательно получаем выражение:
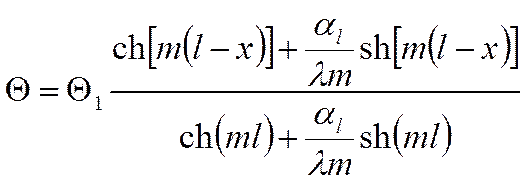
Если тепло отводом от торца можно пренебречь, то:
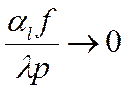
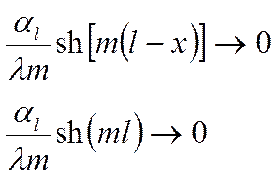

Значение те6мпературы на торце:
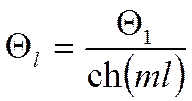
но если ![]() , то мы получим что и раньше:
, то мы получим что и раньше: 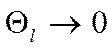 .
.
Определение количества тепла, отводимого стержнем конечной длины в окружающую среду.
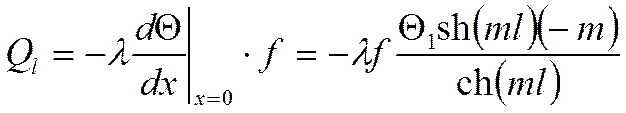
 |
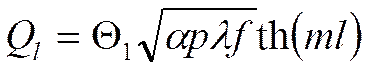 (*)
(*)
Если: ![]() ,
то:
,
то: 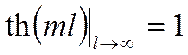 .
.
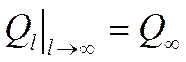
Теплопередача через ребристую плоскую стенку.
Представим себе плоскую стенку, оребрённую по стороне с малым коэффициентом теплоотдачи:
![]()
![]()
![]()
![]()
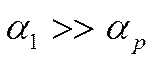
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
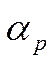 - в среде, омывающей ребро.
- в среде, омывающей ребро.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - длина ребра.
- длина ребра.
![]()
![]()
![]()
![]()
![]() - ширина ребра.
- ширина ребра.
![]()
![]()
![]()
![]()
![]() (рёбра тонкие).
(рёбра тонкие).
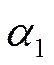
![]()
![]()
![]()
![]() -площадь ребра.
-площадь ребра.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -периметр.
-периметр.
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]() -площадь поперечного сечения.
-площадь поперечного сечения.
Из выражения (*), как частный случай следует:
![]()
![]()
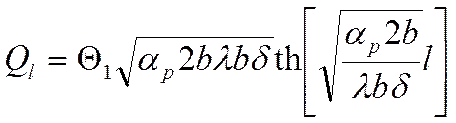
Умножим на 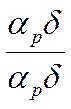 Умножим на
Умножим на ![]()
А так же, умножив всё
выражение на ![]() , получим:
, получим:
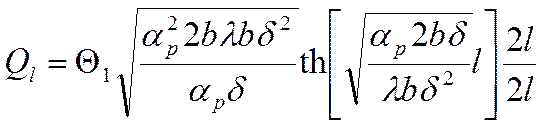
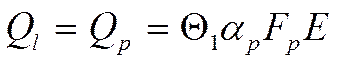
Где:![]() -
коэффициент эффективности ребра..
-
коэффициент эффективности ребра.. ![]()
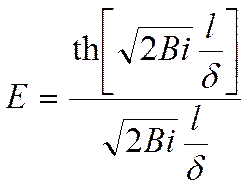 где:
где: 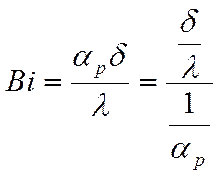 - число Био.
- число Био.
![]() Физический смысл числа
Био: число
Био характеризует соотношение величин термических сопротивлений ребра и
теплоотдачи от ребра.
Физический смысл числа
Био: число
Био характеризует соотношение величин термических сопротивлений ребра и
теплоотдачи от ребра.
Тонким телом называется тело, находящееся в окружающей среде при
Некоторое геометрическое тело, помещённое в одну среду может называться тонким, а в другой среде – уже нет.
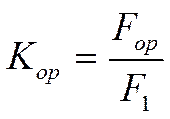
![]() -
площадь гладкой поверхности.
-
площадь гладкой поверхности.
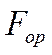 -
площадь оребрённой стороны:
-
площадь оребрённой стороны:
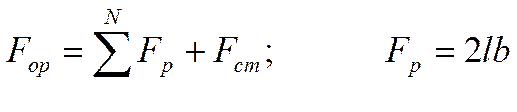
![]()
![]()
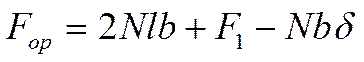
![]()
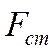
Общее количество тепла, предаваемого через ребристую стенку:
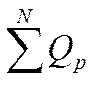
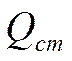
![]()
![]()
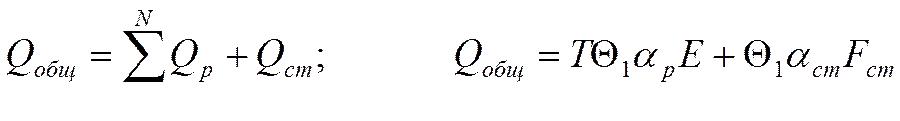
В общем случае ![]() стенки не совпадает с
стенки не совпадает с ![]() ребра и его надо рассчитывать.
ребра и его надо рассчитывать.
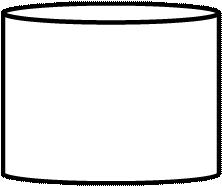
Круглое ребро постоянной толщины. Теплоотвод от круглого ребра.
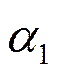 |
![]()
![]()
![]() - внутри
трубы.
- внутри
трубы.

![]() - со
стороны ребра.
- со
стороны ребра.
![]()
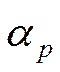
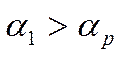
![]()
![]()
![]()

![]() - внутренний радиус
ребра.
- внутренний радиус
ребра.
![]()
![]()
![]()
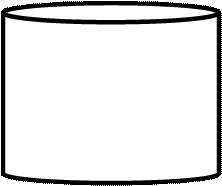
![]() - наружный радиус ребра.
- наружный радиус ребра.
![]() Известно:
Известно: 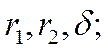
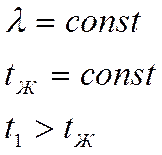
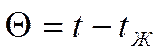
Отвод тепла от рёбер идёт в окружающую среду. Отвод тепла или подвод по интенсивности может быть разным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.