Сигналы. Классификация и терминология. Периодические сигналы. Дискретные спектры. Непериодические сигналы. Сплошные спектры. Идеализированные сигналы. Обобщённые спектры

Глава 2.       Сигналы.

2.1.  Классификация и терминология.

Различают следующие сигналы:

Детерминированные и случайные (шумы). Часто мы имеем дело со смесью.

Аналоговые и дискретные (цифровые).

Периодические и непериодические. Очень строго говоря, можно утверждать, что периодических сигналов в природе нет. Любой сигнал когда-то начинается (включается), изменяет свои параметры. Поэтому иногда употребляют термин квазипериодические.

Видео и радиосигналы.

Узкополосные и широкополосные.

Много примеров мы будем обсуждать позже, и эта терминология станет более понятной. Дальше мы будем рассматривать, в основном, аналоговые детерминированные сигналы. Математической моделью такого сигнала является функция , непрерывная или кусочно-непрерывная.

Зачем нужно разлагать сложные сигналы по гармоническим функциям мы уже обсуждали (и ещё к этому вернёмся). Перейдём к реализации этого метода.

2.2.  Периодические сигналы. Дискретные спектры.

Пусть сигнал  есть вещественная периодическая функция с периодом . Из курса математики известно, что любую периодическую функцию, удовлетворяющую условиям Дирихле (конечное число разрывов первого рода и интервалов монотонности на периоде) можно разложить в ряд Фурье. Любой реальный сигнал, который мы можем принять за периодический, удовлетворяет этим условиям. Выпишем сразу различные формы разложений, вещественные и комплексную.

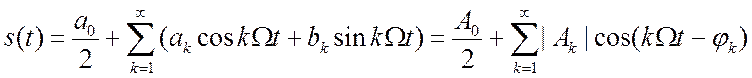;                (2.1)

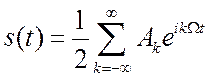.                                                                                        (2.1а)
Здесь: 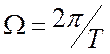 ; ; 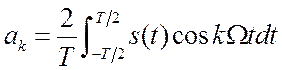 ; 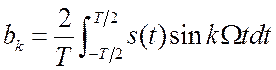.  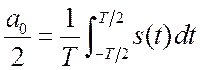- среднее за период или постоянная составляющая.
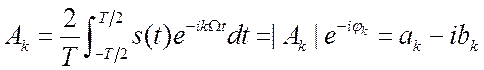 - комплексные коэффициенты.
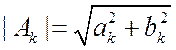;  ;  ;  ;   ( есть сопряжённое значение).  есть четная функция частоты ,  - нечетная.

Коэффициенты написанных разложений определяют амплитуды отдельных гармонических составляющих сигнала. Они и образуют спектр сигнала . Периодические сигналы имеют дискретный спектр, содержащий различные гармоники частоты . Приведём несколько примеров разложений.

2.2.1.  Последовательность прямоугольных импульсов.

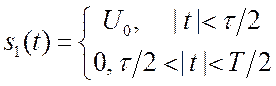 на периоде, рис.2.1. Последовательность характеризуется тремя параметрами:  - величина скачка, амплитуда;  - длительность импульса и  - период. Начало отсчёта выбрано так, что  функция четная. При этом  будут вещественны.

    

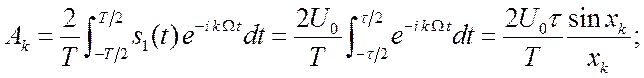
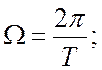
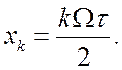
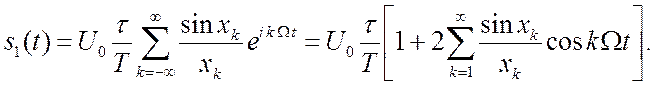                        (2.2)
 - постоянная составляющая. Спектр сигнала изображён на рис.2.2. Пусть скважность . Тогда амплитуды гармоник кратных 4 равны нулю (рис.2.2а). Уменьшим  в два раза. Тогда  (рис.2.2б). Наконец, уменьшим и  в два раза. Снова , но теперь увеличилась  в два раза (рис.2.2в).

Интересный спектр получается, когда   (, меандр). Исчезают все чётные гармоники (кроме нулевой), нечетные убывают монотонно обратно пропорционально номеру, рис.2.3.

2.2.2.  Последовательность пилообразных импульсов.

, когда . Рис. 2.4. Здесь два параметра  и . Функция определена как нечётная, поэтому  будут мнимыми.

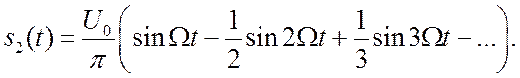                                 (2.3)
Амплитуды гармоник убывает монотонно (как ), рис. 2.5.

2.2.3.  Последовательность треугольных импульсов.

, когда , рис.2.1.  , при  нечётном, и , при  чётном. 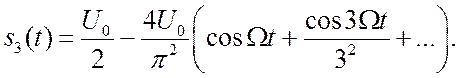     (2.4)
Здесь амплитуды нечётных гармоник тоже убывают монотонно, но быстрее чем в предыдущем примере (как ), поскольку сама функция непрерывна, рис.2.6.

2.2.4.  Подведём итог.

Периодические сигналы имеют дискретный спектр (линейчатый). Он содержит гармоники основной частоты , определяемой периодом. Спектры, подобные приведённым, часто называют гармоническими. Теоретически спектры периодических последовательностей импульсов содержат бесконечное число гармоник. Реальные сигналы представлены конечным набором. Очень важно научиться оценивать ширину спектра сигнала. Существуют два распространённых способа (критерия) оценки. До первой нулевой гармоники, как в первом примере при большой скважности, или пока амплитуды гармоник не станут меньше некоторого заданного уровня от максимальной, например 0.1. К этому вопросу мы ещё вернёмся.

2.3.  Непериодические сигналы. Сплошные спектры.

Из курса математики известна следующая теорема. Если функция  удовлетворяет условиям Дирихле на любом конечном интервале  и 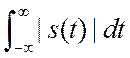 ограничен, то  и  связаны преобразованиями Фурье.

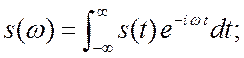
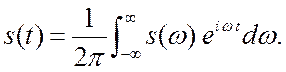                                            (2.5)
Первое равенство даёт прямое преобразование. Оно определяет функцию , которую называют плотностью спектра сигнала . Второе равенство есть обратное преобразование от спектральной функции к временной. Преобразования взаимно однозначны. Пишут: . Если  напряжение, то  имеет размерность вольт сек/рад. Амплитуда гармонических составляющих в малом спектральном интервале от  до  бесконечно мала - .

Таким образом, непериодические (ограниченные во времени) сигналы имеют сплошной спектр, определяемый функцией . Неограниченные во времени непериодические сигналы могут иметь дискретный спектр. Например, сумма двух гармонических сигналов с частотами  и , находящимися в иррациональном отношении, непериодична, но имеет дискретный спектр (две линии).