Сигналы. Классификация и терминология. Периодические сигналы. Дискретные спектры. Непериодические сигналы. Сплошные спектры. Идеализированные сигналы. Обобщённые спектры, страница 6

При более сложном законе изменения  поступают так. Функцию  представляют набором гармонических составляющих. Для каждой из них спектр легко находится. Затем всё суммируют. Полоса частот, занимаемая таким сложным сигналом, будет определяться максимальной частотой  в спектре функции .

Амплитудная модуляция используется в радиовещании, в телевидении для передачи сигнала изображения и во многих других случаях.

2.7.2.  Угловая модуляция.

Пусть . Теперь амплитуда  постоянна. Гармонические вещественные сигналы  и  часто представляют в виде проекций вращающегося вектора  (комплексный сигнал ) на оси  и . Амплитуда сигнала есть длина вектора, а фаза, аргумент - это угол . Сигнал  мы тоже можем считать проекцией вектора, рис. 2.22. Тогда круговая частота  есть угловая скорость вращения вектора, т.е. . Обычно пишут . Если  и  не зависят от времени, то частота постоянна и равна . В противном случае, частота меняется независимо от того, будет  функцией времени или . Поэтому деление угловой модуляции на частотную и фазовую очень условно. Сигналы и спектры похожи.

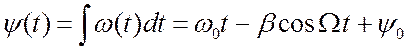В качестве примера рассмотрим сигнал, частота которого меняется по гармоническому закону. Пусть . Здесь:  есть средняя частота;  - частота модуляции;  - девиация частоты (максимальное отклонение от средней). Обычно . Введем индекс модуляции  и вычислим аргумент . Положим . Тогда .                                                   (2.21)
Это выражение можно интерпретировать как сигнал, у которого частота  “постоянна”, а меняется дополнительная фаза , где  - девиация фазы. После элементарных тригонометрических преобразований получим .

Для анализа спектрального состава воспользуемся известными разложениями ( - функции Бесселя):

…;

 .
После новых преобразований будем иметь:

                                    .            (2.22)
Спектр получился дискретный, симметричный относительно частоты . В спектре присутствует основная гармоническая составляющая с частотой  (она может и отсутствовать, если ) и комбинационные боковые с частотами  ( - целое). Ряд бесконечен, однако функции Бесселя начинают очень быстро убывать с ростом номера функции , когда он станет больше аргумента . Поэтому ряд фактически конечен.

Характерный вид спектра при малых и больших значениях  приведён на рисунках 2.23а и 2.23б. При малых значениях  () спектр очень похож на спектр сигнала с амплитудной модуляцией. Ширина спектра примерно равна . Когда , приближённо можно считать, что в спектре представлены  линия. Поэтому ширина спектра будет , т.е. равна удвоенной девиации.

Частотная модуляция тоже очень широко используется при передаче информации, и, в частности, в радиовещании и телевидении. Радиовещательные сигналы с частотной модуляцией имеют полосу порядка 200 КГц, а несущую частоту - десятки и сотни МГц. Снова мы имеем узкополосный сигнал.

2.7.3.  Сопряженные сигналы.

Узкополосные сигналы находят очень широкое применение. Разработан даже специальный аппарат анализа таких сигналов. Рассмотрим очень коротко этот вопрос.

Узкополосный сигнал можно записать таким образом. , причём амплитудная функция  меняется медленно по сравнению с быстро осциллирующим вторым множителем. Из функции  обычно выделяют главное слагаемое , как в выражении (2.21) для угловой модуляции, и пишут . Теперь и функцию  можно тоже считать медленно меняющейся по сравнению с . Особенности поведения  и  иначе выражают так; эти функции мало меняются за период частоты заполнения .

Амплитудно-модулированный сигнал, как мы убедились, есть типичный пример узкополосного сигнала. Для определённости будем строить рассуждения на примере таких сигналов. В большинстве случаев интерес представляет не весь сигнал , а только амплитудная функция  (или  при угловой модуляции). Именно она содержит интересующую нас информацию, сигнал с модулирующей частотой . Возникает проблема найти  в любой момент времени по заданному сигналу . Однако, по одному сигналу  однозначно определить  невозможно. В общее выражение входит ещё и функция , которая тоже неизвестна. Приближённо определить  в дискретные моменты времени можно, взяв, например, экстремальные значения сигнала , рис. 2.26. Но этого недостаточно.