Для реальной гребенчатой функции ![]() амплитуды гармоник
амплитуды гармоник ![]() ,
а следовательно и копии спектра (пунктир на рисунке), уменьшаются с ростом
номера
,
а следовательно и копии спектра (пунктир на рисунке), уменьшаются с ростом
номера ![]() . Однако, при правильном выборе
длительности стробирующих импульсов, убывание идёт очень медленно.
. Однако, при правильном выборе
длительности стробирующих импульсов, убывание идёт очень медленно.
2.9.3. Переход от дискретного сигнала к аналоговому.
Часто возникает
необходимость после обработки дискретного сигнала перейти снова к аналоговому.
Для этого надо устранить периодичность спектра, отфильтровав все
"копии" исходного спектра с помощью фильтра нижних частот - ФНЧ
(стробирование по частоте). Такой фильтр представляет собой аналоговое устройство,
четырёхполюсник, и характеризуется своим коэффициентом передачи ![]() , где
, где ![]() и
и ![]() есть отдельные спектральные составляющие
сигналов на входе и выходе. Пусть ФНЧ имеет идеальную характеристику
есть отдельные спектральные составляющие
сигналов на входе и выходе. Пусть ФНЧ имеет идеальную характеристику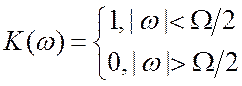 . На вход фильтра мы подаём дискретный
сигнал
. На вход фильтра мы подаём дискретный
сигнал ![]() . Тогда спектр сигнала на выходе
. Тогда спектр сигнала на выходе ![]() . Сам сигнал мы получим, сделав обратное
преобразование Фурье.
. Сам сигнал мы получим, сделав обратное
преобразование Фурье. 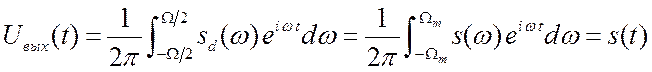 . (2.31)
. (2.31)
Здесь мы учли, что ![]() , а спектр дискретного сигнала на
промежутке интегрирования (на периоде) равен спектру аналогового. При этом от
других копий периодического спектра в интервал интегрирования ничего не
добавится.
, а спектр дискретного сигнала на
промежутке интегрирования (на периоде) равен спектру аналогового. При этом от
других копий периодического спектра в интервал интегрирования ничего не
добавится.
В итоге, получили
снова аналоговый сигнал ![]() . Мы его просто
преобразовали в дискретную форму и обратно. Но это только на бумаге всё хорошо,
всё просто. В реальной ситуации будут искажения сигнала за счёт конечной длительности
стробирующих импульсов, неидеальности ФНЧ и других причин. Не будем
останавливаться на деталях. Нам сейчас важны, прежде всего, идеи.
. Мы его просто
преобразовали в дискретную форму и обратно. Но это только на бумаге всё хорошо,
всё просто. В реальной ситуации будут искажения сигнала за счёт конечной длительности
стробирующих импульсов, неидеальности ФНЧ и других причин. Не будем
останавливаться на деталях. Нам сейчас важны, прежде всего, идеи.
2.9.4. Дискретное Z преобразование.
Это преобразование широко используется для дискретных сигналов. Оно играет для них такую же роль, как преобразование Фурье или Лапласа для аналоговых сигналов. Остановимся на этом очень коротко.
Пусть задан
дискретный сигнал ![]() последовательностью
значений
последовательностью
значений ![]() , конечной или бесконечной. Поставим в
соответствие последовательности функцию комплексной переменной
, конечной или бесконечной. Поставим в
соответствие последовательности функцию комплексной переменной ![]() .
. 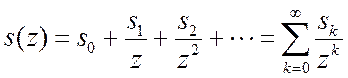 .
(2.32)
.
(2.32)
Здесь мы считаем, что сигнал ![]() при
при ![]() , поэтому
, поэтому ![]() . Эту
сумму, если она существует, и называют
. Эту
сумму, если она существует, и называют ![]() преобразованием
дискретного сигнала
преобразованием
дискретного сигнала ![]() . В
математике такие ряды называют
производящей функцией для последовательности
. В
математике такие ряды называют
производящей функцией для последовательности ![]() .
.
Приведём примеры. Короткий импульс (один
отсчёт). ![]() . Импульс
длительности
. Импульс
длительности ![]() .
. 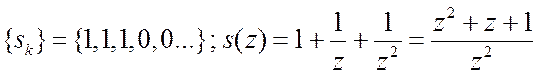 .
.
Ступенчатая функция в аналоговой области. 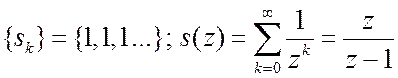 . Ряд
сходится при любых
. Ряд
сходится при любых ![]() в кольце
в кольце ![]() .
.
В принципе, мы можем сделать ![]() преобразование и для аналогового сигнала
преобразование и для аналогового сигнала ![]() , задав интервал дискретизации. Сначала мы
найдём последовательность
, задав интервал дискретизации. Сначала мы
найдём последовательность ![]() , а по ней -
, а по ней - ![]() .
.
Как
совершить обратное преобразование и найти последовательность ![]() по функции
по функции ![]() ? Очень
просто. Умножаем обе части равенства (2.32) на
? Очень
просто. Умножаем обе части равенства (2.32) на ![]() и
интегрируем в области сходимости по замкнутому контуру, охватывающему все
особенности функции
и
интегрируем в области сходимости по замкнутому контуру, охватывающему все
особенности функции ![]() . Она аналитична в кольцевой
области
. Она аналитична в кольцевой
области ![]() . Теперь пользуемся теоремой Коши.
. Теперь пользуемся теоремой Коши. 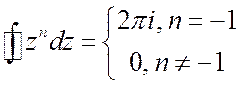 . В результате получим:
. В результате получим:
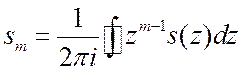 .
(2.33)
.
(2.33)
Это и есть обратное ![]() преобразование. Замечательное свойство
функции
преобразование. Замечательное свойство
функции ![]() состоит в том, что она однозначно
определяет всю совокупность отсчётов, конечную или бесконечную.
состоит в том, что она однозначно
определяет всю совокупность отсчётов, конечную или бесконечную.
В заключение,
проиллюстрируем связь ![]() преобразования с
преобразованиями Фурье и Лапласа. Пусть мы имеем дискретный сигнал
преобразования с
преобразованиями Фурье и Лапласа. Пусть мы имеем дискретный сигнал 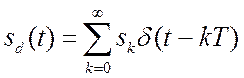 . Преобразуем это равенство по Лапласу.
. Преобразуем это равенство по Лапласу. 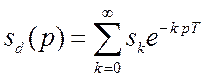 . Отсюда мы получим
. Отсюда мы получим ![]() преобразование,
если положим
преобразование,
если положим ![]() . Если же
. Если же ![]() , то
, то 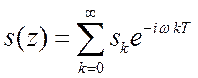 будет преобразованием Фурье сигнала
будет преобразованием Фурье сигнала ![]() .
.
Связь оказалась довольно простая. Она даёт возможность проводить аналогии между характеристиками аналоговых и дискретных сигналов и устройств.
Свойства ![]() преобразования очень похожи на свойства
преобразования Фурье. Приведём некоторые примеры. Линейность. При смещении
сигнала
преобразования очень похожи на свойства
преобразования Фурье. Приведём некоторые примеры. Линейность. При смещении
сигнала ![]() на
один шаг
на
один шаг ![]() вправо (запаздывание),
вправо (запаздывание), ![]() умножается на
умножается на ![]() (на
(на ![]() в аналоговой области).
в аналоговой области).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.