Формулы (2.5) часто получают из формулы (2.1)
комплексного ряда Фурье для периодических сигналов, устремляя период к
бесконечности (![]() ).
).
Тогда: ![]() ;
; ![]() -
текущая частота;
-
текущая частота; ![]() , но
, но ![]() .
.
2.3.1. Полезные свойства преобразования Фурье.
1. Симметрия прямого и обратного преобразования.
2. Если функция ![]() вещественна,
то
вещественна,
то ![]() есть чётная функция частоты
есть чётная функция частоты ![]() , а
, а ![]() -
нечётна. Как следствие,
-
нечётна. Как следствие, ![]() - чётная функция
- чётная функция ![]() ,
, ![]() -
нечётная
-
нечётная
3. Для вещественной функции ![]() обратное
преобразование может быть выполнено только по положительным частотам.
обратное
преобразование может быть выполнено только по положительным частотам. ![]() .
.
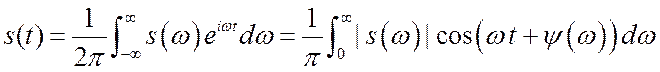 .
.
Как и в ряде Фурье, отрицательные частоты
появляются при комплексной форме записи, но такая форма, обычно, удобнее.
4. Линейность преобразования. Если ![]() , а
, а ![]() , то
, то
![]() имеет спектр
имеет спектр ![]() . Очень
важное свойство.
. Очень
важное свойство.
5. Масштабное преобразование. Если ![]() , то каков спектр сигнала
, то каков спектр сигнала ![]() , где
, где ![]() вещественно и положительно? Ответ:
вещественно и положительно? Ответ: ![]() . При сжатии сигнала спектр расширяется.
. При сжатии сигнала спектр расширяется.
6. Спектр производной. Если ![]() дает
дает
![]() , то каков спектр сигнала
, то каков спектр сигнала ![]() ? Ответ:
? Ответ: ![]() . Поэтому множитель
. Поэтому множитель ![]() называют оператором дифференцирования.
Внеинтегральный член при интегрировании по частям исчезает за счет убывания
называют оператором дифференцирования.
Внеинтегральный член при интегрировании по частям исчезает за счет убывания ![]() , при
, при ![]() .
.
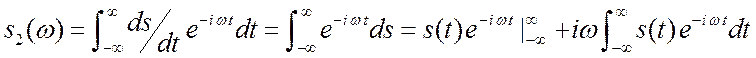 .
.
7. Если ![]() , то
каков спектр сигнала
, то
каков спектр сигнала 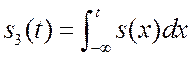 ? Ответ:
? Ответ: ![]() ,
т.е.
,
т.е. ![]() есть оператор интегрирования. Доказательство основывается
на предыдущем свойстве, поскольку
есть оператор интегрирования. Доказательство основывается
на предыдущем свойстве, поскольку ![]() .
.
8. Если ![]() , то
каков спектр запаздывающего сигнала
, то
каков спектр запаздывающего сигнала ![]() ?
?
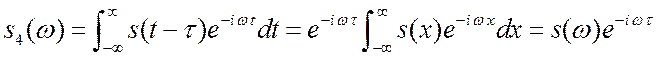
![]() . (2.6)
. (2.6)
При запаздывании сигнала на время ![]() , спектр умножается на
, спектр умножается на ![]() . Меняются только фазы гармонических
составляющих;
. Меняются только фазы гармонических
составляющих; ![]() не
меняется. Очень важное свойство.
не
меняется. Очень важное свойство.
9. Если ![]() , то
каков спектр сигнала
, то
каков спектр сигнала ![]() ?
?
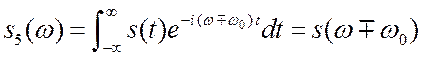 . Произошёл сдвиг спектра. Последние два свойства
иллюстрируют симметрию преобразования Фурье.
. Произошёл сдвиг спектра. Последние два свойства
иллюстрируют симметрию преобразования Фурье.
10. Если ![]() и
и ![]() , то какому сигналу соответствует произведение
спектров
, то какому сигналу соответствует произведение
спектров ![]() ?
?
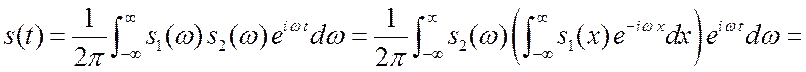
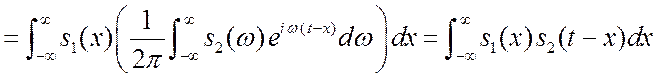 .
.
В итоге, произведение спектров соответствует свертке функции ![]() и
и ![]() .
.
В силу симметрии преобразования, спектр произведения функции ![]() , есть свёртка спектров
, есть свёртка спектров ![]() и
и ![]() .
. 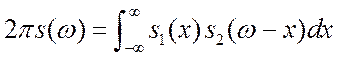 .
.
2.3.2. Энергетические соотношения.
1. Периодические сигналы. Напишем среднюю за период
мощность на единичном сопротивлении (![]() - напряжение или ток).
- напряжение или ток). 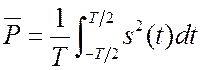 .
. ![]() есть среднеквадратичное
или эффективное значение
есть среднеквадратичное
или эффективное значение ![]() . Теперь выразим
. Теперь выразим ![]() через амплитуды гармоник.
через амплитуды гармоник.
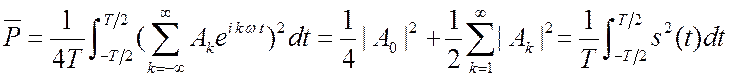
Последнее равенство есть математическое условие полноты или замкнутости системы
тригонометрических функций. Физический смысл этого равенства таков. Средняя
мощность сигнала ![]() равна сумме средних мощностей
отдельных гармоник. Для доказательства этого равенства надо перемножить ряды и
учесть ортогональность отдельных гармоник.
равна сумме средних мощностей
отдельных гармоник. Для доказательства этого равенства надо перемножить ряды и
учесть ортогональность отдельных гармоник. 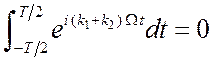 , если
, если
![]() . Когда
. Когда ![]() , интеграл дает
, интеграл дает ![]() . Таких
интегралов будет два (
. Таких
интегралов будет два (![]() ).
).
2. Непериодические сигналы. Теперь рассмотрим полную
энергию сигнала на единичном сопротивлении. Для реальных сигналов эта величина
должна быть
конечной. 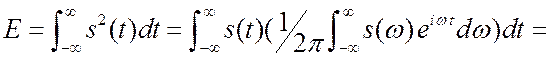
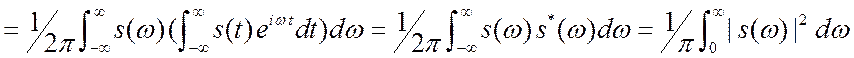 .
.
Получили известное в математике равенство Парсеваля. С физических позиций опять
получилась аддитивность энергии отдельных гармонических составляющих. Величина ![]() есть спектральная плотность энергии.
есть спектральная плотность энергии.
2.4.1. Примеры спектров видеоимпульсов. Прямоугольный импульс.
![]()
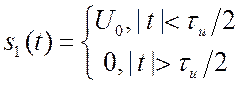 . Рис.2.7.
. Рис.2.7. 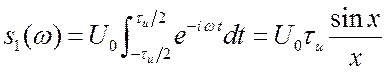 ,
(2.7)
,
(2.7)
где 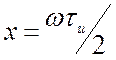 . Функция
. Функция ![]() очень
часто встречается в физических приложениях. Спектр прямоугольного импульса
изображён на рис. 2.8. Произведение
очень
часто встречается в физических приложениях. Спектр прямоугольного импульса
изображён на рис. 2.8. Произведение ![]() есть “площадь”
импульса.
есть “площадь”
импульса.
Для характерных спектров подобного типа за ширину
спектра сигнала часто принимают интервал ![]() до
первого нуля функции
до
первого нуля функции ![]() . В данном случае
. В данном случае ![]() . Отсюда
. Отсюда ![]() или
или ![]()
![]() . Очень простое соотношение.
Здесь
. Очень простое соотношение.
Здесь ![]() - это уже обычная частота (в Герцах). Чем короче
импульс, тем шире его спектр. Следовательно, чем быстрее и больше мы хотим
передать информации, тем короче должны быть импульсы при её кодировании, тем
шире будет спектр такого сообщения.
- это уже обычная частота (в Герцах). Чем короче
импульс, тем шире его спектр. Следовательно, чем быстрее и больше мы хотим
передать информации, тем короче должны быть импульсы при её кодировании, тем
шире будет спектр такого сообщения.
Если мы будем повторять этот импульс с периодом ![]() , то в пределе получим периодическую
последовательность импульсов и линейчатый спектр (гармоники). Можно найти
амплитуду гармоник
, то в пределе получим периодическую
последовательность импульсов и линейчатый спектр (гармоники). Можно найти
амплитуду гармоник ![]() , зная
, зная ![]() ?
Очень легко.
?
Очень легко.
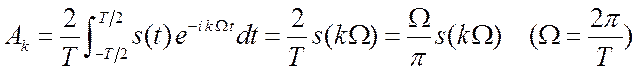 (2.8)
(2.8)
Линии спектра окажутся как бы вписанными в изображённую функцию. Чем больше
период, тем чаще будут идти линии. Поэтому в учебниках изображают и анализируют
подробно именно спектры одиночных импульсов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.