Глава 3. Теория линейных цепей.
Будем считать параметры цепей ![]() и
и ![]() постоянными
величинами и на начальном этапе анализа использовать символический метод. Обсудим
сначала некоторые общие особенности цепей, получим общие формулы, а затем перейдём
к рассмотрению конкретных примеров цепей, которые находят широкое применение.
постоянными
величинами и на начальном этапе анализа использовать символический метод. Обсудим
сначала некоторые общие особенности цепей, получим общие формулы, а затем перейдём
к рассмотрению конкретных примеров цепей, которые находят широкое применение.
3.1. Мостовая цепь.
На этом примере, рис. 3.1, мы выясним некоторые общие
закономерности и вспомним терминологию. Цепь имеет 6 ветвей, 4 узла, 7
различных контуров, но независимых всего три. Столько надо ввести независимых
токов или напряжений, столько надо написать уравнений. Как определить число
независимых контуров ![]() ? Приведём два распространённых
правила: 1.
? Приведём два распространённых
правила: 1. ![]() равно минимальному числу разрывов цепи,
чтобы ликвидировать все замкнутые контуры. 2.
равно минимальному числу разрывов цепи,
чтобы ликвидировать все замкнутые контуры. 2. ![]() . Для
этого примера
. Для
этого примера ![]() .
.
Напомним последовательность действий при составлении системы уравнений контурных токов.
1. Определяем число независимых контуров. В данном случае 3.
2. Выбираем три независимых контура и вводим три тока,
![]() . Каждый новый контур должен содержать
какой-то новый элемент, который раньше не фигурировал. В результате, все
элементы должны быть задействованы. Выбор контуров и направлений токов указан
на приведённом рисунке.
. Каждый новый контур должен содержать
какой-то новый элемент, который раньше не фигурировал. В результате, все
элементы должны быть задействованы. Выбор контуров и направлений токов указан
на приведённом рисунке.
3. Задаём положительные направления токов в каждом выбранном контуре. Часто рекомендуют выбирать направления обхода по часовой стрелке.
4. Задаём полярность генераторов (тоже условно) и рисуем у генераторов стрелки (от минуса к плюсу).
5. Составляем уравнения. Сумма падений напряжения на всех элементах контура, за счёт всех токов, должна равняться сумме ЭДС. При этом ЭДС суммируется со знаком плюс, если направления стрелок у генератора и у тока совпадают. В противном случае ставится минус.
Для данного примера
получим следующую систему уравнений. (3.1)
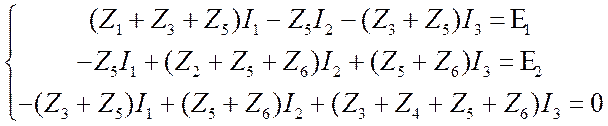 ;
;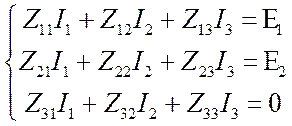 .
.
Здесь: ![]() . Остальные равенства уже очевидны. Ещё
короче записывают систему в матричном обозначении.
. Остальные равенства уже очевидны. Ещё
короче записывают систему в матричном обозначении. ![]() , где
, где 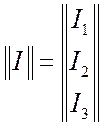 и
и 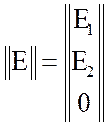 есть
векторы (матрица столбец), а
есть
векторы (матрица столбец), а ![]() - полная матрица
сопротивлений (
- полная матрица
сопротивлений (![]() ), образованная элементами
), образованная элементами ![]() . Элемент
. Элемент ![]() называют
собственным сопротивлением контура
называют
собственным сопротивлением контура ![]() . Общий элемент двух
контуров
. Общий элемент двух
контуров ![]() называют сопротивлением связи этих
контуров.
называют сопротивлением связи этих
контуров.
Поделим первое уравнение
системы (3.1) на ![]() . Получим полное сопротивление
первого контура в сложной цепи, как сумму собственного сопротивления и вносимого
за счёт других контуров.
. Получим полное сопротивление
первого контура в сложной цепи, как сумму собственного сопротивления и вносимого
за счёт других контуров. 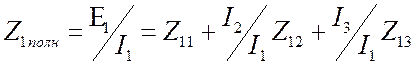 .
. ![]() есть собственное сопротивление первого
контура. Всё остальное – вносимое.
есть собственное сопротивление первого
контура. Всё остальное – вносимое. 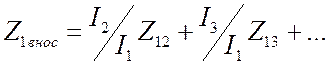 . Сопротивления
. Сопротивления ![]() определяются только параметрами цепи и не
зависят от токов. Вносимое сопротивление зависит и от токов.
определяются только параметрами цепи и не
зависят от токов. Вносимое сопротивление зависит и от токов.
3.1.1. Решение системы.
Приведём сразу готовый
результат из курса математики. Пусть ![]() есть главный
определитель системы (3.1). Если в цепи есть потери (электрическая энергия
переходит в тепловую), то
есть главный
определитель системы (3.1). Если в цепи есть потери (электрическая энергия
переходит в тепловую), то ![]() и система (3.1) имеет
единственное решение.
и система (3.1) имеет
единственное решение. 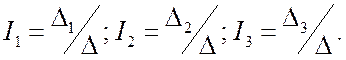 Определитель
Определитель ![]() получается из
получается из ![]() заменой
столбца с номером
заменой
столбца с номером ![]() вектором
вектором ![]() .
.
Рассмотрим 2 случая. 1.
Пусть ![]() . Найдём
. Найдём 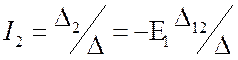 .
Здесь
.
Здесь ![]() - минор определителя
- минор определителя ![]() . Минор
. Минор ![]() получается
из
получается
из ![]() вычёркиванием строки с номером
вычёркиванием строки с номером ![]() и столбца с номером
и столбца с номером ![]() , на пересечении которых стоит элемент
, на пересечении которых стоит элемент ![]() .
.
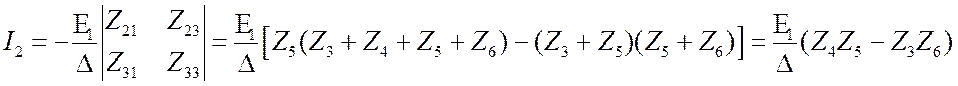
Отсюда следует, что ![]() при условии «баланса» моста
при условии «баланса» моста ![]() . Этим часто пользуются на практике. 2.
Пусть теперь
. Этим часто пользуются на практике. 2.
Пусть теперь ![]() . Найдём
. Найдём 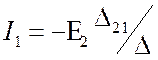 . Покажите
самостоятельно, что
. Покажите
самостоятельно, что 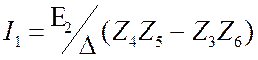 . Теперь
. Теперь ![]() при
«балансе».
при
«балансе».
3.1.2. Обратимость цепи (взаимность).
Отметим одно очень важное
общее свойство матрицы ![]() системы (3.1). Для любой линейной
(не содержащей зависимых генераторов) цепи
системы (3.1). Для любой линейной
(не содержащей зависимых генераторов) цепи ![]() . Это и
есть проявление теоремы взаимности. Доказательство этой теоремы приводится в
курсах электродинамики. В теории цепей это свойство просто отмечается и
проверяется на примерах. Покажем теперь, что из приведённого равенства для
элементов матрицы, следует равенство миноров
. Это и
есть проявление теоремы взаимности. Доказательство этой теоремы приводится в
курсах электродинамики. В теории цепей это свойство просто отмечается и
проверяется на примерах. Покажем теперь, что из приведённого равенства для
элементов матрицы, следует равенство миноров ![]() .
Сделаем это для рассмотренного примера. Доказательство в общем случае
совершенно аналогично.
.
Сделаем это для рассмотренного примера. Доказательство в общем случае
совершенно аналогично. 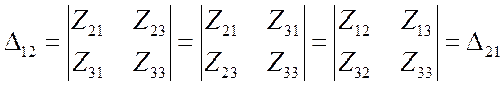 . Сначала мы заменили
строки столбцами, а затем учли равенства
. Сначала мы заменили
строки столбцами, а затем учли равенства ![]() . Итак,
для любой линейной цепи
. Итак,
для любой линейной цепи ![]() .
.
Для рассмотренного
примера это даёт: ![]() . Говорят, что взаимное
сопротивление контуров 1 и 2 не зависит от направления передачи энергии. Это
свойство имеет место для любых двух контуров линейной цепи и формулируется
часто следующим образом. Пусть мы имеем линейный пассивный четырёхполюсник.
Назовём входной контур первым, а выходной – вторым. На рис. 3.2 изображены два
варианта включения генератора и приведены необходимые обозначения. Например,
. Говорят, что взаимное
сопротивление контуров 1 и 2 не зависит от направления передачи энергии. Это
свойство имеет место для любых двух контуров линейной цепи и формулируется
часто следующим образом. Пусть мы имеем линейный пассивный четырёхполюсник.
Назовём входной контур первым, а выходной – вторым. На рис. 3.2 изображены два
варианта включения генератора и приведены необходимые обозначения. Например, ![]() есть ток во втором контуре, когда источник
находится в первом. Меняются местами только идеальные генератор и амперметр. Тогда:
есть ток во втором контуре, когда источник
находится в первом. Меняются местами только идеальные генератор и амперметр. Тогда:
![]() .
(3.2)
.
(3.2)
Это равенство и отражает взаимность или обратимость цепи. Доказывается оно в общем случае точно так же, как в приведённом примере.
3.2. Теорема об эквивалентном генераторе.
Имеем активный линейный
двухполюсник, нагруженный на сопротивление ![]() , рис.
3.3а. Требуется определить ток в нагрузке. Пусть
, рис.
3.3а. Требуется определить ток в нагрузке. Пусть ![]() есть
напряжение холостого режима (
есть
напряжение холостого режима (![]() ) активного
двухполюсника, а
) активного
двухполюсника, а ![]() - сопротивление этого
двухполюсника, когда все внутренние источники выключены (пассивный
двухполюсник). Теорема даёт простой ответ:
- сопротивление этого
двухполюсника, когда все внутренние источники выключены (пассивный
двухполюсник). Теорема даёт простой ответ: 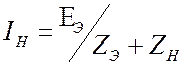 .
(3.3)
.
(3.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.