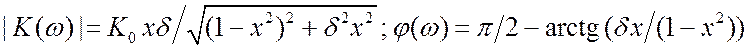Теория линейных цепей. Мостовая цепь. Теорема об эквивалентном генераторе. Матричная теория линейных четырёхполюсников. Физическая осуществимость цепей, страница 14

. Легко показать, что  имеет максимум при , независимо от величины , а  и есть это максимальное значение. Уравнение для граничных частот полосы пропускания ПФ на уровне 0,71 выглядит так, . Оно имеет такое решение. 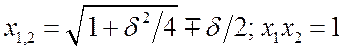. Отсюда относительная полоса пропускания . Поскольку для  фильтров , такие фильтры получаются широкополосные. Оценка коэффициента прямоугольности даёт значение 0,1. Фильтры получаются плохого качества. Несмотря на это, они находят широкое применение.

Когда  и  (), то два варианта цепи имеют одинаковые коэффициенты передачи, . При этом, говорят об эквивалентности этих цепей по коэффициентам передачи. Но надо иметь в виду, что строгой эквивалентности нет, поскольку входные и выходные сопротивления различаются. Анализ этого выражения мы проведём в следующем параграфе.

Рассмотрим теперь очень типичный случай, когда  (на несколько порядков). При этом обычно . Примем эти условия. Тогда . Коэффициенты передачи двух вариантов ПФ теперь практически совпадают. . Таким образом, порядок следования дифференцирующей и интегрирующей цепочек перестаёт играть роль. Мы можем считать, что эти цепочки как бы разделены буферным устройством и не влияют друг на друга, рис. 3.46в. Тогда мы можем перемножать их коэффициенты передачи. 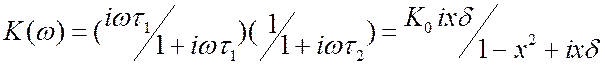. Здесь , . Фильтр получается широкополосным.

Зависимость коэффициента передачи от частоты для широкополосных цепей лучше изображать, используя логарифмический масштаб по оси частот. В противном случае, низкочастотная часть характеристик будет очень сжата, как в следующем примере. Пусть, для определённости, , а  (два порядка). Тогда типичные зависимости изображены на рис. 3.47. При этом, анализ характеристик можно проводить независимо на низких и высоких частотах, используя соответственно либо коэффициент передачи дифференцирующей цепочки, либо интегрирующей.

3.8.6. Цепь Вина.

Это типичный полосовой фильтр, рис. 3.48а. Он не пропускает постоянную составляющую напряжения за счёт конденсатора , а за счёт элементов  и  обеспечивается убывание  на высоких частотах. Таким образом, на низких частотах работают элементы  и , образуя дифференцирующую цепь, а на высоких – другие два элемента дают интегрирование. В рассматриваемой цепи на выходе уже есть сопротивление и ёмкость, поэтому мы можем считать, что нагрузка уже учтена, и полагать . Цепь имеет вид делителя из двух сопротивлений. Используя обозначения предыдущих примеров, будем иметь: ; . Здесь .

Для цепи Вина типична ситуация, когда все постоянные времени одинаковы. При этом: .
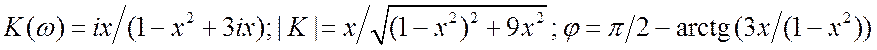. (3.46) Эти характеристики приведены на рис. 3.48. Они очень похожи на характеристики колебательного контура с малой добротностью (1/3).  на частоте  максимален и равен 1/3, а сдвиг фазы равен нулю. Полосовые фильтры предыдущих примеров при  имеют точно такие же характеристики.

3.8.7.  Переходные характеристики цепей второго порядка.

Для всех рассмотренных цепей второго порядка в знаменателях коэффициентов передачи стоит одинаковый полином . Уравнение  называют характеристическим. Корни этого уравнения определяют полюса коэффициента передачи, а следовательно, реакцию цепи на импульсное воздействие.

При решении конкретных задач чаще пользуются преобразованием Лапласа и переходят от обычной (вещественной) частоты  к комплексной частоте  (поворот комплексной плоскости  на  против часовой стрелки). Удобно опять перейти к безразмерной комплексной частоте . Основное преимущество перехода к комплексной частоте состоит в том, что характеристическое уравнение для  всегда имеет вещественные (положительные) коэффициенты. Такое уравнение более привычно и удобно, поскольку его корни или вещественные, или образуют комплексно сопряжённые пары.

Обратимся к цепям второго порядка и рассмотрим сразу оба варианта уравнения.    или  . Корни этих уравнений таковы: 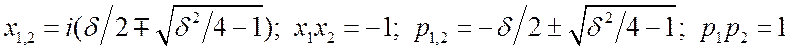. Для  цепей , поэтому оба корня на плоскости  вещественны и отрицательны. На комплексной плоскости  (или ) корни лежат на мнимой оси в верхней полуплоскости. Ситуация изображена на рис. 3.49. Когда , получается один кратный корень. Это предельный случай для  цепей.