 При движении материальной точки
координаты с течением времени изменяются, т.е. являются функциямивремени.
Скалярные уравнения: x = x(t);
При движении материальной точки
координаты с течением времени изменяются, т.е. являются функциямивремени.
Скалярные уравнения: x = x(t);
y = y(t); z = z(t) (1.1) в общем случае являются кинематическими уравнениями движения точки. Система уравнений (1.1) эквивалентна векторному уравнению r = r (t) .
Положение точки в пространстве можно описать с помощью полярных координат r,Θ,φ (рис.1).

|
свободы.
Траекторией движения называют линию, описываемую движущейся точкой. Пусть материальная точка перемещается
по кривой из положения А в положение В
(рис. 2). Тогда дуга АˇВ будет траекторией, а длина этой дуги ∆s будет длиной пути. Длина пути ∆s представляет собой скалярную функцию времени ∆s= ∆s (t). Начальное положение материальной точки задается радиусом-вектором r0,а конечное - радиусом-вектором r. Вектор Δr = r –r0 (приращение радиуса-вектора за рассматриваемый промежуток времени) называется перемещением. При прямолинейном перемещении | Δr | = ∆s.
 Скорость
СкоростьБыстрота и направление движения точки характеризуется
скоростью. Скорость векторная величина. Пусть точка перемещается из
положения А в положение В (рис.3). В момент времени t
положение материальной точки характеризует радиус-вектор r0. За малый
промежуток времени Δt точка прошла путь Δs ![]() до положения В и совершила элементарное перемещение Δr.
Вектором средней скорости
называют отношение
до положения В и совершила элементарное перемещение Δr.
Вектором средней скорости
называют отношение
‹ v› = Δr /Δt [м/c]
Направление ‹v› совпадает с направлением Δr.
Мгновенной скоростью vназывают предел отношения приращения радиуса-вектора точки Δrк промежутку времени Δt, стремящемуся к нулю
v= lim Δr /Δt = dr/dt ,
Δt→0
т.е. v есть первая производная радиуса-вектора по времени. В пределе при Δt→0, секущая АВ совпадает с касательной и, следовательно, мгновенная скорость v направлена по касательной в каждой точке траектории.
По мере уменьшения Δtпуть ∆s будет приближаться к значению модуля перемещения |Δr|, поэтому модуль мгновенной скорости будет равен
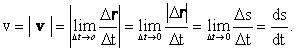
![]()
Из полученного выражения видно, что ds = dt. Путь s, пройденный за время Δt, найдем, интегрируя выражение ds = v dt в пределах от t до t+ Δt
s =![]()
В случае равномерного движения (v = const) s = vt. В самом общем случае, когда скорость является функцией времени v = v(t), путь, пройденный за время Δt = t2 –t1, определяется интегралом
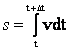 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.