Цифровые устройства и микропроцессоры: Учебное пособие, страница 9

Если все термы, входящие в нормальную форму имеют одинаковый и максимальный ранг, равный числу переменных функции - n, то такая  форма называется совершенной. При этом, минтерм называется констинтуентой (составляющей) единицы (КЕ), а макстерм -  конституентой нуля (КН).

                      -     это  СДНФ

                   -  это СКНФ

Таким образом, совершенная дизъюнктивная нормальная форма - есть дизъюнкция конституент единицы, а СКНФ - есть конъюнкция конституент нуля.

Совершенные формы составляются по таблице истинности функции. СДНФ составляется по такому правилу:  для каждого набора переменных,  на котором функция истинна, записывают минтерм ранга  n , в котором с отрицанием берутся переменные имеющие нулевые значения на данном наборе. Все минтермы объединяют дизъюнктивно.

Пусть, например, имеем произвольную функцию трёх переменных, заданную такой  таблицей  истинности  (рис. 1.18):

№\X	a	b	c	f
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

 

      Рисунок 1.18 – Таблица истинности произвольной функции

      Для номеров наборов  N= 1, 3, 6 и 7 получаем  следующую СДНФ:

                                          

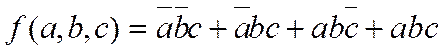
СКНФ также записывают по таблице истинности по правилу:

для  каждого  набора  переменных, на  котором функция ложна, записывают макстерм ранга n,  в  котором с отрицанием берутся переменные, имеющие единичные  значения на данном наборе. Все макстермы объединяют конъюнктивно. Тогда, для этой же функции  с  номерами  наборов N = 0, 2, 4 и 5  получаем СКНФ:

                                          

Очевидно, что СДНФ и СКНФ полностью дуальны.

Для компактной записи функций используют числовую форму,  в  которой задаются только номера наборов. Числовая форма для СДНФ:

                                                    

Числовая форма для СКНФ:

                                                                    

1.4  Минимизация функций

1.4.1  Задача минимизации

Пусть требуется построить логическую схему, которая реализует следующую таблицу истинности (рис. 1.19):

№\X	a	b	c	f
0	0	0	0	0
1	0	0	1	1
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	0
6	1	1	0	1
7	1	1	1	1

             Рисунок 1.19 – Таблица истинности  для логической схемы

        Для реализации схемы запишем  СДНФ:

                                            

        Каждый минтерм реализован своим конъюнктором. Инверсии выполнены на входах, чтобы не пользоваться дополнительными инверторами и не загромождать схему. Получаем (рис. 1.20):

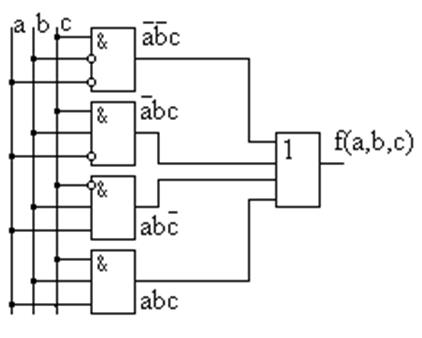
            Рисунок 1.20 – Схемная реализация  таблицы истинности (рис.1.19)

Используя законы алгебры логики, попытаемся упростить исходную функцию.

Для этого используем  вынесение за скобки:        

Очевидно, что реализация такой формулы значительно проще.

Логическая формула с наименьшим числом логических связей называется минимальной.

Таким образом, получаем  минимальную дизъюнктивную нормальную форму (МДНФ) и, соответственно, - МКНФ.

Процесс отыскания минимальной формы называется минимизацией логической функции или просто минимизацией.

Минимизировать функции можно тремя методами:

       1)   расчетным путем, используя законы алгебры логики,