Навигационные параметры и изолинии. Аналитический метод определения места судна с помощью изолиний. Линеаризация навигационных функций и ее геометрическая интерпретация. Априорная и апостериорная оценка точности обсервации, страница 8

Система уравнений не нарушится, если левую и правую часть каждого из уравнений системы (59) или (62) умножить на одно и то же число.

В матричном виде эта операция соответствует умножению системы  слева на матрицу вида:

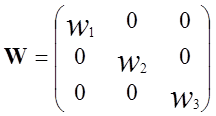,                          (68)

элементами которой являются величины, обратные СКП измерений (1/m). После выполнения такого умножения система (62) будет иметь вид:

                      (69)

Последовательность вывода ничем не отличается от вывода изложенного в предыдущем параграфе.

Выражение для Q, (64) ,перепишется так:

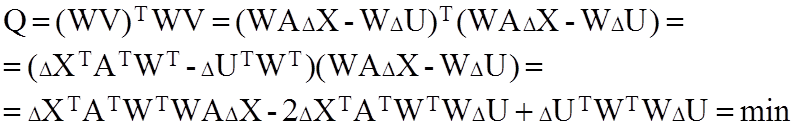(70)

Обозначим 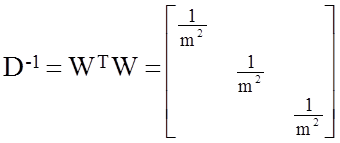   ,         (71)

- весовая матрица, обратная ковариационной матрице погрешностей

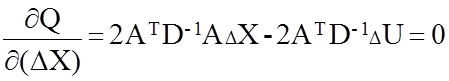          (72)

Система нормальных уравнений запишется так:

                      (73)

а решение будет иметь вид:

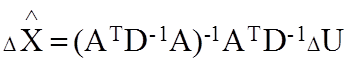(74)

Если элементы матрицы (69) равны, это означает, что измерения равноточные и (74) превращается в (67). Формула (73) носит более общий характер, чем (66).

Вероятнейшая точка, полученная по формуле (74) - является средневзвешенным значением измеренных параметров.

После того как система нормальных уравнений будет решена, определяют обсервованные координаты. При необходимости применяется итерационная процедура Ньютона. Итерационная процедура Ньютона применяется для уменьшения погрешностей линеаризации изолиний. Обычно, определив место, необходимо провести анализ точности измерений.

1.5.4  Алгоритм решения задачи расчета координат в случае избыточных измерений.

- измерить навигационные параметры Uo₁, и Uo₂„

- найти счислимые значения Uc₁ и Uc₂ этих же навигационных параметров по счислимым координатам (j_с и l_с) на момент измерений;

- вычислить приращения навигационных параметров DU₁ и DU₂, рассчитать модули градиентов g₁, g₂ ,

- вычислить коэффициенты системы уравнений;

- сформировать матрицу частных производных;

- сформировать ковариационную матрицу погрешностей измерений;

- найти матрицу коэффициентов нормальных уравнений;

- найти ковариационную матрицу погрешностей координат;

- найти псевдообратную матрицу

- найти вектор приращения координат;

- вычислить географические координаты обсервованного места:

j_o = j_c +Dj

l_j = l_c + Dw secj_т

Если приращения географических координат отвечают требованиям точности, то решение задачи заканчивается, если нет, то полученные координаты записывают как счислимые, и цикл счета повторяется. Процедуру выполняют до тех пор, пока требования не будут удовлетворены. Обычно во всех алгоритмах определения места судна предусмотрена данная циклическая схема расчета. Как правило, итерационный процесс включает не более трех циклов.

1.5.5  Свойства метода наименьших квадратов

Изучив основные технические приемы использования МНК в обработке навигационных измерений, полезно сделать анализ основных свойств метода.

Во-первых, необходимо различать статистические и нестатистические свойства. Ясно, что в какой-то эпизодической обсерва­ции по избыточному числу линий положения МНК выступает, как формальный и наиболее простой математический аппарат, используя который можно однозначно фиксировать точку отно­сительно фигуры погрешностей при условии, что систематичес­ких погрешностей в измерениях нет или они включены в опре­деляемые переменные, т. е. в векторDХ. В этом случае фигура погрешностей с точностью до случайных погрешностей измеряе­мых параметров находится в окрестности истинной точки. Поэтому разовая обсервация, привязанная к фигуре по­грешностей, с точностью до случайных погрешностей из­меряемых навигационных параметров будет находить­ся в окрестности истинной точки (рис. 19).

В пределах доверитель­ного интервала, являющего­ся суммой доверительных интервалов вершин много­угольника погрешностей, размеры фигуры погрешнос­тей определяются случайны­ми погрешностями измере­ний, а поэтому ее размеры не могут служить характе­ристикой точности измере­ний. В этой области малая фигура не обязательно дол­жна быть ближе к истинной точке. Систематические же погреш­ности измерений приводят к четкой аналитической зависимости размеров фигуры и расстояния до истинной точки.

Теперь есть смысл говорить о вероятностно-статистических характеристиках МНК, если результаты измерений удовлетво­ряют следующим условиям:

значения коэффициентов линий положения известны точно;

результаты измерений содержат лишь случайные составля­ющие погрешностей;

погрешности измерений имеют нормальный закон распреде­ления.

Свойства МНК таковы.

1. Несмещенность оценки, т. е. математическое ожидание оценки, равна истинному значению. Это свойство имеет явно асимптотический характер и может наблюдаться в большой со­вокупности измерений.

2. Состоятельность оценки, т. е. оценка при увеличении п,, стремится к истинному значению параметра по вероятности:

Р{|Х-Х|>x}® 0, е® 0.

3. Эффективность оценки (оценка называется эффективной, если она в данном классе оценок имеет минимальную диспер­сию).

4. Линейная процедура при нормальном законе распреде­ления погрешностей измерений определяет и нормальность оценки. 180

5. При нормальном законе распределения МНК является частным случаем метода максимального правдоподобия.

6. Линейность обработки делает МНК очень чувствитель­ным к наличию промахов, систематических погрешностей изме­рений и к неравноточности навигационных параметров.