1. Измеряем компасные пеленги двух навигационных ориентиров: КП1=209°; КП2=332°. Поправка компаса DК=+2°. С учетом поправки компаса получаем истинные пеленги ИП1=211°; ИП2=334°.
2. Счислимые координаты jс=54°26,7' N,lс=13°38,4' Е. С карты от этой точки сняты счислимые расстояния: Dс1 =6,5 мили; Dс2 =5,8 мили и счислимые пеленги Пс1 =207°; Пс2 =337°
3. Рассчитываем приращения навигационных параметров:
DП1=211°—207°=+4°; DП2=334° —337°= —3°.
4. Вычисляем модули и направления градиентов:
g1=573°/Dc1 =8,82...°/миля; g2=57,3°/Dc2=9,88..°/миля;
t1 =207,0° — 90° = 117°,t2 = 337° — 90° =247°.
5. Рассчитываем коэффициенты уравнений (6.46) по формулам выражения (6.45):
 a1=
-4,00; b1=+7,86; l1= -4,00;
a1=
-4,00; b1=+7,86; l1= -4,00;
a2= -3,86; b2=-9.09; l2= +3.00;
6. Выполняем решение уравнений поправок координат:
Dj = -12,78/66,7 = - 0,19 » - 0,2 мили (-2 кбт);
Dw =+ 27,44/66,7 = +0,41»+-04 мили (+4 кбт).
7. Рассчитываем обсервованные координаты:
jo=54°26,7' - 0,2'=54°26,5' N;
lo=13°38,4'+0,4/ (1,72) = 13° 39,1’ E.
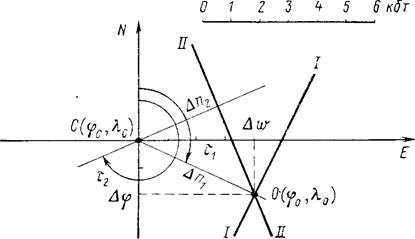
Рис. 18. Графоаналитическое решение примера
Основной недостаток определения места судна по двум линиям положения заключается в том, что отсутствует какой-либо способ контроля правильности, точности и надежности обсервации.
Число навигационных измерений при определении места судна очень существенно влияет как на точность определения места, так и на саму вычислительную процедуру. Если измеряются 2 навигационных параметра и определяются 2 координаты, то говорят, что в задаче отсутствует избыточность, т.е. система уравнений (32), как правило, совместна.
Отсутствие избыточности измерений приводит к неконтролируемому влиянию различных видов погрешностей на результат, а особенно опасны грубые промахи и систематические погрешности.
Для получения более надежной обсервации применяют избыточные навигационные измерения.
Пусть для определения координат места судна измерены три навигационных параметра (n=3), определить же нужно, две координаты (k=2). Говорят, что в этой ситуации избыточность r= n-k=1.
Система уравнений линий положения запишется так:
a11Dx1 + a12Dx2 = Du1
a21Dx1 + a22Dx2 = Du2 , (59)
a31Dx1 + a32Dx2 = Du3
или в более лаконичном матричном виде:
A DX =DU (60)
где:
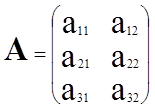 -
таблица коэффициентов при
неизвестных;
-
таблица коэффициентов при
неизвестных;
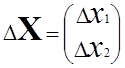 -
матрица (вектор) неизвестных;
-
матрица (вектор) неизвестных;
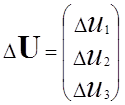 -
матрица (вектор) измерений.
-
матрица (вектор) измерений.
В этой системе количество неизвестных k меньше, чем количество уравнений n. Решение любых двух уравнений соответствует только этой паре и при подстановке этого решения в третье тождества не будет. Такая система называется несовместной, т.е. решение пары уравнений не совместно с третьим.
Для того чтобы сделать систему совместной, добавим в правую часть вектор невязок V , приводящий систему в соответствие
a11Dx1 + a12Dx2 = Du1+v1
a21Dx1 + a22Dx2 = Du2+v2 , (61)
a31Dx1 + a32Dx2 = Du3+v3
Или в матричном виде
![]() (62)
(62)
Так как получить решение, удовлетворяющее всем уравнениям невозможно, то ставится задача по-другому: найти единственное решение, при котором сумма квадратов невязок была бы минимальна. Это требование формализуется так:
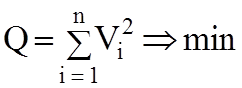 (63)
(63)
Отсюда происходит название рассматриваемого метода - МЕДОД НАИМЕНЬШИХ КВАДРАТОВ (МНК).
Пусть систематическая погрешность одинакова для всех n измерений.
Для решения системы (60), запишем выражение (63) в матричном виде Q=VTV, выразив вектор невязок V из (62). При раскрытии операции используется правило матричного исчисления (AB)T=BTAT:
![]()
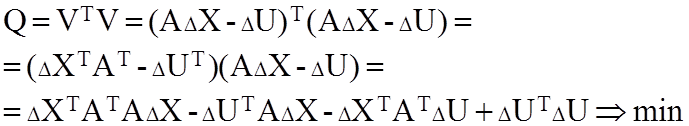 ,(64)
,(64)
Так как Q является числом, то и слагаемые также являются числами. Легко показать, что два слагаемых равны между собой.
DX T A T DU = (DU T A DX ) T.
Тогда выражение для Q можно записать так:
Q = DXT AT A DX - 2 DXT A T DU +DUT DU Þ min (65)
Взяв производную от выражения (65) по вектору неизвестных и приравняв ее к нулю, находим формулу для решения системы (60):
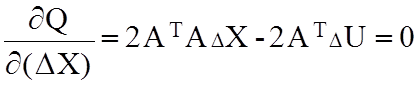
![]() (66)
(66)
Система (66) называется системой нормальных уравнений.
Решение выглядит так:
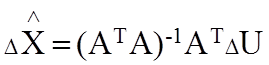 (67)
(67)
В соответствии общей процедурой метода Ньютона, где отыскиваются поправки к приближенным значениям искомых параметров, расчет по (2.12) является частью итерационной процедуры, как и в случае с двумя измерениями. Знак “^” над вектором искомых величин означает, что решение получено с применением критерия оптимальности Q.
В терминологии МНК, оптимальная точка называется вероятнейшей точкой.
В предыдущем параграфе никак не оговаривались погрешности измеряемых навигационных параметров, так как они считались равноточными, т.е. имеющими одинаковые средние квадратические погрешности - m.
В общем случае измерения навигационных параметров не являются равноточными, т.е. их средние квадратические погрешности могут отличаться, что и происходит на практике, если навигационные измерения выполнены различными приборами или различными наблюдателями. В этом случае с вероятно-статистической точки зрения есть основания больше доверять тому измерению, которое имеет наименьшие погрешности. Поэтому вполне естественно считать, что поправки, применяемые для формирования матрицы невязок, должны быть обратно пропорциональны соответствующим СКП измерений, т.е. величинам mi. Естественно, что вероятнейшая точка, полученная по МНК должна быть ближе к той линии положения, которая точнее, "вес" которой больше.
Величина pi = 1/mi2 называется весом измерения и характеризует относительную точность измерений, входящих в группу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.