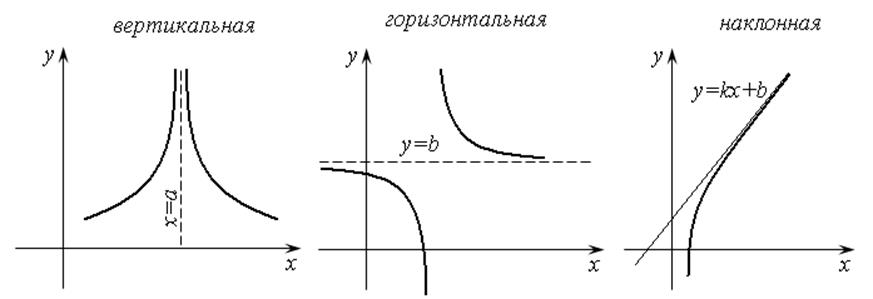
Рис. 14.11
Проще всего найти вертикальную асимптоту.
Она, как правило, присутствует в точках разрыва 2-го рода, где один или оба
односторонние предела не существуют, т. е. 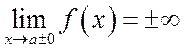 .
Это точки, где знаменатель обращается в нуль или граничные точки области
определения функции.
.
Это точки, где знаменатель обращается в нуль или граничные точки области
определения функции.
Например, функция  имеет
2 точки разрыва 2-го рода:
имеет
2 точки разрыва 2-го рода: ![]() и
и ![]() . Подробно ее поведение мы обсудили в
примере 14.3. Односторонние пределы равны
. Подробно ее поведение мы обсудили в
примере 14.3. Односторонние пределы равны ![]() ,
поэтому делаем вывод, что прямые
,
поэтому делаем вывод, что прямые ![]() и
и ![]() являются вертикальными асимптотами.
являются вертикальными асимптотами.
Функция 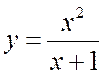 имеет одну точку
бесконечного разрыва:
имеет одну точку
бесконечного разрыва: ![]() , поэтому прямая
, поэтому прямая ![]() – вертикальная асимптота. Функция
– вертикальная асимптота. Функция ![]() при
при ![]() имеет
множество точек разрыва 2-го рода
имеет
множество точек разрыва 2-го рода 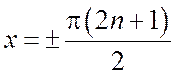 , где
, где ![]() и, следовательно, столько же
вертикальных асимптот. Вспомните график тангенсоиды, и вам все станет понятным.
и, следовательно, столько же
вертикальных асимптот. Вспомните график тангенсоиды, и вам все станет понятным.
Функция 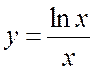 имеет
одну точку, подозрительную на разрыв:
имеет
одну точку, подозрительную на разрыв: ![]() .
В ней и знаменатель обращается в нуль и
.
В ней и знаменатель обращается в нуль и ![]() .
То есть
.
То есть  . Действительно прямая
. Действительно прямая ![]() , т.е. ось
, т.е. ось ![]() ,
будет левосторонней (располагающейся слева от графика) асимптотой (рис. 14.12).
,
будет левосторонней (располагающейся слева от графика) асимптотой (рис. 14.12).
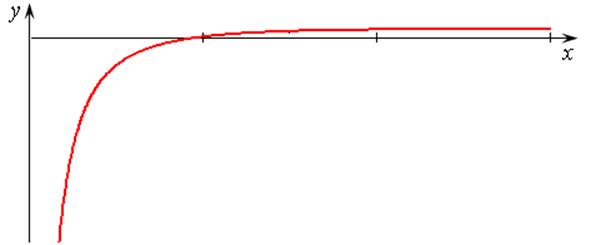
Рис. 14.12
Практически также просто определить наличие горизонтальной
асимптоты. Если функция ![]() при
при
![]() имеет предел, равный числу
имеет предел, равный числу ![]() , то прямая
, то прямая ![]() является
горизонтальной асимптотой.
является
горизонтальной асимптотой.
Например: функция  имеет
горизонтальную асимптоту, т.к.
имеет
горизонтальную асимптоту, т.к.  , т. е. при
, т. е. при ![]() прямая
прямая ![]() служит
нижней горизонтальной асимптотой, график функции располагается выше оси
служит
нижней горизонтальной асимптотой, график функции располагается выше оси ![]() . Если
. Если ![]() ,
то ось
,
то ось ![]() является верхней горизонтальной асимптотой,
т.к.
является верхней горизонтальной асимптотой,
т.к. 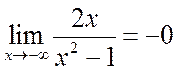 (рис. 15.4).
(рис. 15.4).
Функция 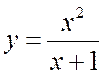 не имеет
горизонтальной асимптоты, т. к.
не имеет
горизонтальной асимптоты, т. к. 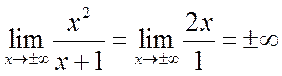 .
.
И, наконец, функция 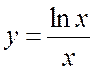 при
при
![]() также имеет горизонтальную асимптоту
также имеет горизонтальную асимптоту
![]() (верхнюю или нижнюю?).
(верхнюю или нижнюю?).
Определить характер стремления к своей асимптоте проще
всего, найдя предел разности 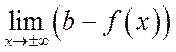 . Если он больше
нуля, то асимптота проходит выше графика функции, меньше – ниже.
. Если он больше
нуля, то асимптота проходит выше графика функции, меньше – ниже.
Именно этот прием – нахождения разности между точками,
лежащими на прямой и графиком функции ![]() ,
– лежит в основе определения параметров наклонной асимптоты.
,
– лежит в основе определения параметров наклонной асимптоты.
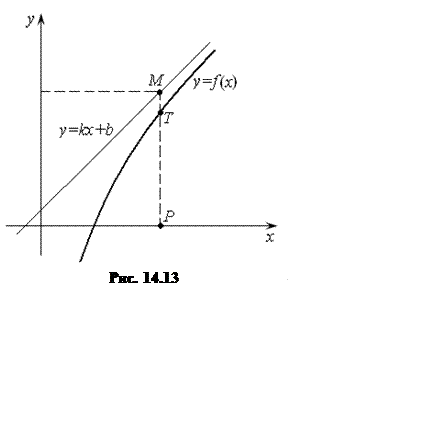
На рисунке 14.13 приведен график функции ![]() , имеющий наклонную асимптоту. Это
значит, что разность
, имеющий наклонную асимптоту. Это
значит, что разность ![]() стремится к нулю при неограниченном
удалении от начала координат, т. е. при
стремится к нулю при неограниченном
удалении от начала координат, т. е. при ![]() .
Пусть уравнение асимптоты записано в виде
.
Пусть уравнение асимптоты записано в виде ![]() ,
функции
,
функции ![]() .
.
 Найдем указанную разность значений
Найдем указанную разность значений ![]() при одинаковых значениях аргумента
при одинаковых значениях аргумента ![]() :
:
![]() . (14.3)
. (14.3)
При
![]() эта разность должна стремиться к
нулю, т. е.
эта разность должна стремиться к
нулю, т. е.
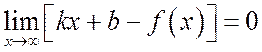 . (14.4)
. (14.4)
Преобразуем
выражение, стоящее под знаком предела. Вынесем ![]() за
скобки, получим:
за
скобки, получим:
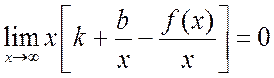 .
.
Для
того, чтобы это произведение было равно нулю, необходимо чтобы хотя бы один
сомножитель был равен нулю. Т.к. ![]() , то только
, то только 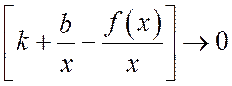 . Но
. Но 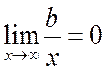 ,
поэтому остается
,
поэтому остается 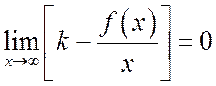 , откуда
, откуда
 .
(14.5)
.
(14.5)
Вернемся к равенству (14.4). Найдем из него ![]() , помня, что предел постоянной равен
самой постоянной:
, помня, что предел постоянной равен
самой постоянной:
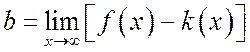 , (14.6),
, (14.6),
где
![]() находится по формуле (14.5).
находится по формуле (14.5).
Если хотя бы один из этих пределов не существует –
график функции ![]() наклонной асимптоты не
имеет. Очевидно, что по тем же формулам можно найти наклонные асимптоты и при
наклонной асимптоты не
имеет. Очевидно, что по тем же формулам можно найти наклонные асимптоты и при ![]() , причем случается, что они не совпадают.
, причем случается, что они не совпадают.
Пример 14.4.
Определить, будет ли функция 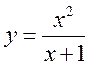 иметь наклонную
асимптоту.
иметь наклонную
асимптоту.
Решение: Воспользуемся формулами (14.5) и (14.6)
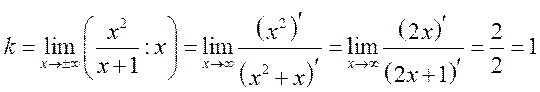 ,
,
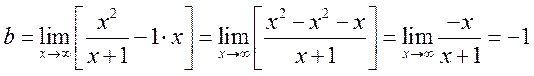 .
.
Таким образом, прямая ![]() является наклонной асимптотой при
является наклонной асимптотой при ![]() .
.
Для
правильного построения графика функции и асимптоты найдем разность ![]() при
при ![]() .
.
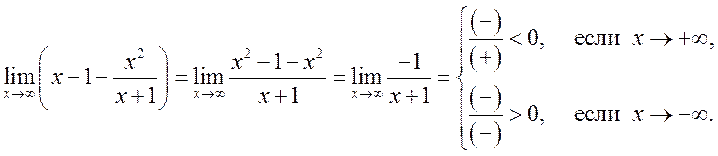
То есть, если ![]() , то асимптота располагается выше
графика функции, если
, то асимптота располагается выше
графика функции, если ![]() , то ниже.
, то ниже.
Строим график, учитывая все предыдущие исследования.
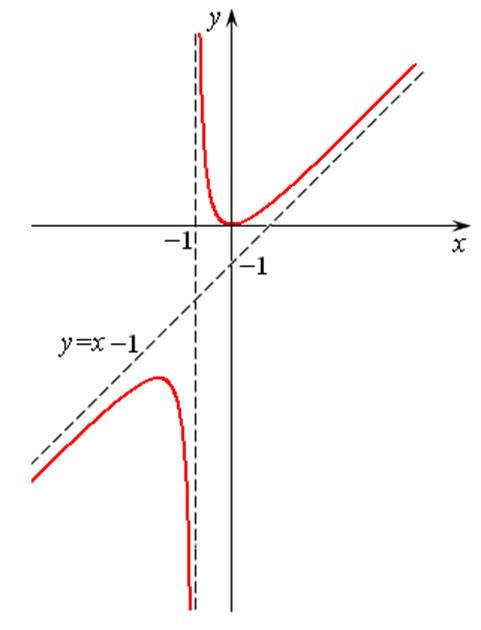
Рис. 14.14
Для закрепление этого большого материала проведем полное исследование функции по плану, означенному в начале лекции:
![]() .
.
1. Область
определения функции: ![]() , точек разрыва нет.
, точек разрыва нет.
2.
Симметрия: ![]() , т. е. данная функция нечетная,
проходит через точку
, т. е. данная функция нечетная,
проходит через точку ![]() ,
, ![]() и
имеет корни, которые можно найти решив уравнение,
и
имеет корни, которые можно найти решив уравнение, ![]() .
Решим это уравнение графически
.
Решим это уравнение графически 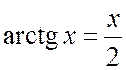 . Построим график
функции
. Построим график
функции ![]() и
и 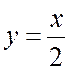 .
Если они пересекутся – то исходная функция имеет корни. График функции
.
Если они пересекутся – то исходная функция имеет корни. График функции ![]() получается симметричным отражением
графика
получается симметричным отражением
графика ![]() относительно прямой
относительно прямой ![]() . Прямую
. Прямую 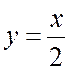 построим
по точкам.
построим
по точкам.
|
|
|
|
0 |
0 |
|
1 |
0,5 |
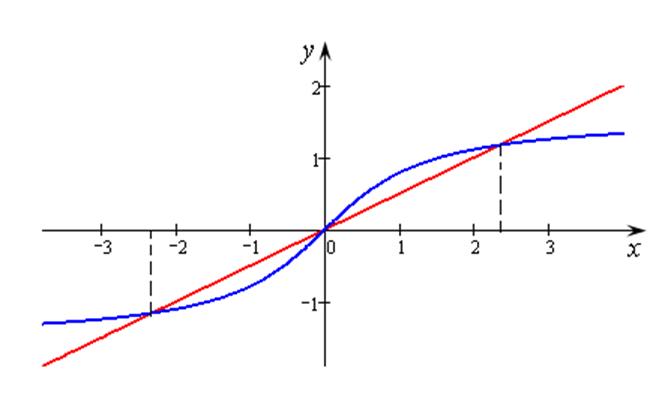
Рис. 14.15
Как видно из рис. 14.15 эти два графика пересекаются в
точках ![]() и
и ![]() ,
то есть корни функции лежат в этих интервалах. Более точно найти корни можно
при помощи метода половинного деления (см. лекцию 10).
,
то есть корни функции лежат в этих интервалах. Более точно найти корни можно
при помощи метода половинного деления (см. лекцию 10).
3. Экстремумы, интервалы возрастания – убывания.
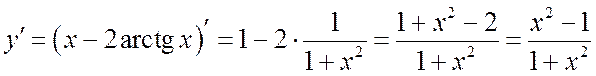 .
.
Тогда
![]() , если
, если ![]() ,
т.е. если
,
т.е. если ![]() и
и ![]() .
Определим знак
.
Определим знак ![]() на каждом из интервалов
на каждом из интервалов ![]() . Данные сведем в таблицу
. Данные сведем в таблицу
|
|
|
вывод |
|
|
|
+ |
возрастает |
|
|
|
0 |
максимум |
0,57 |
|
|
– |
убывает |
|
|
|
0 |
минимум |
–0,57 |
|
|
+ |
возрастает |
Найдем значения исходной функции в экстремальных точках и начертим первый «прибросочный» график (рис. 14.16).
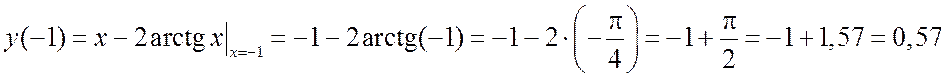 ,
,
![]() в
силу симметрии.
в
силу симметрии.
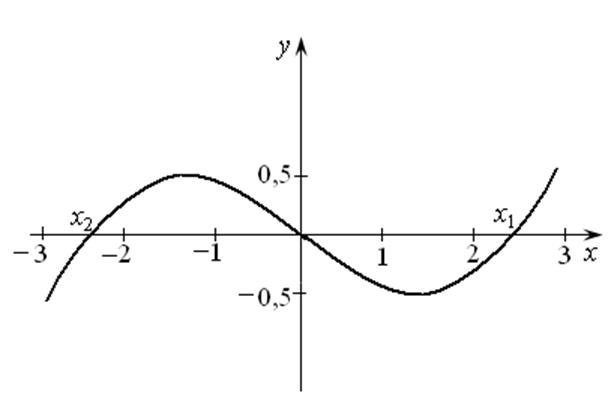
Рис. 14.16
4. Точки перегиба, интервалы выпуклости вогнутости.
Найдем
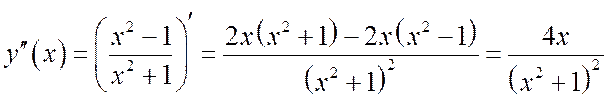 .
.
Тогда
![]() , если
, если ![]() .
.
Составим таблицу знаков для ![]() ,
которая подтверждает наш рис. 15.9.
,
которая подтверждает наш рис. 15.9.
|
|
|
Вывод |
|
|
|
– |
выпуклая |
|
|
0 |
0 |
точка перегиба |
0 |
|
|
– |
вогнутая |
5. Найдем
наклонные асимптоты функции, так как ни вертикальной ни горизонтальной она
иметь не может (почему?), причем учтем, что их в силу симметрии будет две.
Итак, найдем ![]() и
и ![]() для
уравнения
для
уравнения ![]() .
.
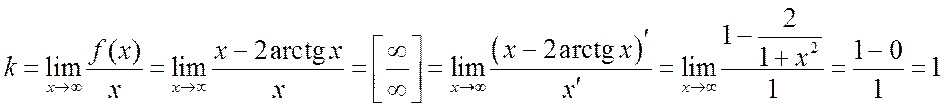 ,
,
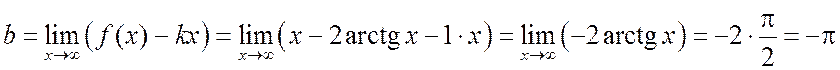 .
.
Здесь
мы учли, что 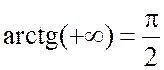 . То есть прямая
. То есть прямая ![]() является правосторонней наклонной
асимптотой
является правосторонней наклонной
асимптотой ![]() .
.
Если ![]() , то коэффициент
, то коэффициент ![]() не изменится, а
не изменится, а ![]() станет равным
станет равным ![]() , потому что
, потому что 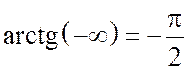 .
Левосторонняя асимптота имеет вид
.
Левосторонняя асимптота имеет вид ![]() . Начертим общий
график (рис. 14.17).
. Начертим общий
график (рис. 14.17).
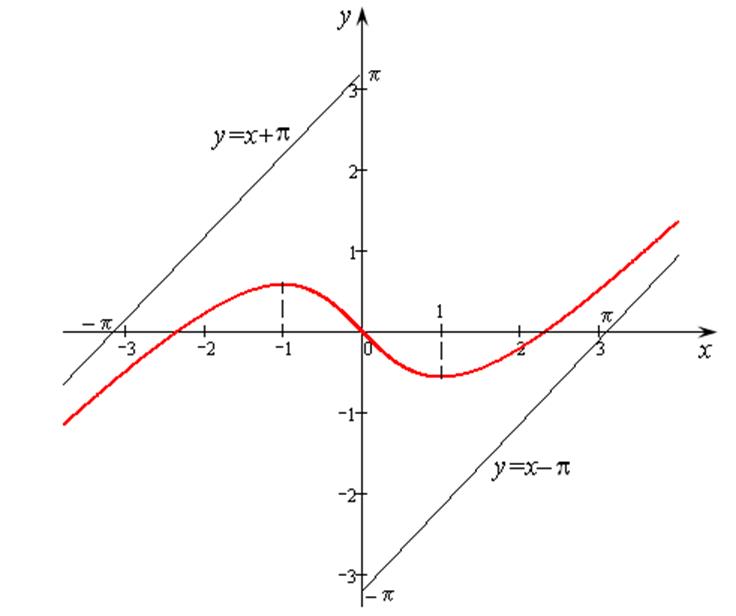
Рис. 14.17
На этом мы закончим тему «Исследование функции методами дифференциального исчисления». Этот материал вам необходим для решения соответствующей задачи контрольного задания.
Следующий материал поможет вам в практической работе при исследовании функций, заданных таблично или графически.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.