Было бы наивно полгать, что все «измышления» (теоремы, правила и т.д.) дифференциального исчисления практичное человечество не смогло поставить себе на службу. Сокровища науки только до поры остаются известными узким специалистам. Приходит время, и ими начинают пользоваться многие, приспосабливая к своим задачам.
Любое явление – конъюнктура рынка, сезонные колебания спроса на товар, прибыль и т.д. – вначале изучаются с количественной стороны, а потом, если это, возможно, описывают функциональной зависимостью, т.е. формулой.
Например, анализ спроса на купальники показал, что он
подчиняется формуле ![]() , где
, где ![]() – некоторые постоянные, не меняющиеся
в течении лет,
– некоторые постоянные, не меняющиеся
в течении лет, ![]() – время (мес.). На
основании приведенной формулы можно выяснить, при каких значениях
– время (мес.). На
основании приведенной формулы можно выяснить, при каких значениях ![]() спрос будет максимальным и каких
именно величин он достигнет, при каких – минимальным и ряд других вопросов.
спрос будет максимальным и каких
именно величин он достигнет, при каких – минимальным и ряд других вопросов.
Именно они входят в понятие «исследование поведение функции». Очевидно, выяснять эти вопросы с помощью самостоятельного сбора информации не всегда разумно, а иногда затруднительно. Поэтому в данной главе покажем общие приемы исследования функций. За основу возьмем аналитический способ задания, а потом, при решении экономических задач, используем табличный и графический способы, как наиболее часто встречающиеся. Все исследования подчиним общему плану, каждый пункт которого будет решать свои задачи, подкрепленные соответствующими теоретическими обоснованиями. Итак, план.
План исследования функции.
1. Область определения функции. Выявление точек разрыва, поведение функции вблизи точек разрыва.
2. Симметрия, точки пересечения с осями координат.
3. Интервалы возрастания – убывания, точки экстремумов (первая производная)
4. Интервалы выпуклости – вогнутости, точки перегиба (вторая производная)
5. Асимптоты: вертикальные, горизонтальные, наклонные.
6. Построение графика.
Некоторые из разделов уже рассматривались в той или иной мере. Вспомним, что знаем и дополним то, чего не знаем.
Область определения функции или область допустимых значений (ОДЗ) рассматривалась в лекции 8 «Функции. Способы задания».
Напомним, что если функция задана аналитически, т. е. с помощью формулы, то соблюдают требования:
1) неотрицательности подкоренного выражения: если ![]() , то
, то ![]() ;
;
2) положительности подлогарифмического выражения: если
![]() , то
, то ![]() ,
и
,
и
3) неравенства нулю знаменателя дроби: если 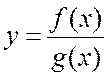 , то
, то ![]() .
.
Например:
1. ![]() ОДЗ
ОДЗ
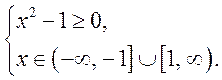
2. 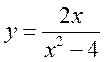 ОДЗ
ОДЗ
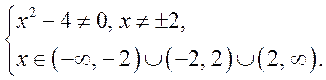
Рассмотрим
последний пример подробнее, определив поведение функции вблизи точек разрыва ![]() и
и ![]() .
Для этого найдем односторонние пределы при
.
Для этого найдем односторонние пределы при ![]() и
и
![]() .
.
 ,
,
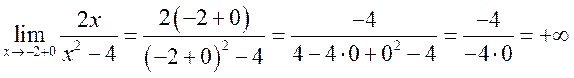 ,
,
 ,
,
 .
.
Нарисуем соответствующий график:
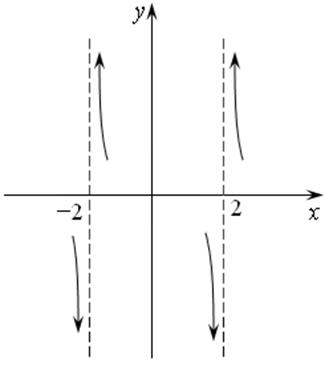
Рис. 14.1.
Как ведет себя функция в остальных точках мы не знаем, поэтому торопиться с общим графиком не будем. Мы исследуем ее по полной программе, в качестве иллюстрирующего примера.
За симметрию графика относительно осей или начала координат отвечает четность и нечетность функции.
Функция ![]() называется четной,
если для нее справедливо равенство
называется четной,
если для нее справедливо равенство![]() и нечетной,
если
и нечетной,
если ![]() .
.
Четные функции симметричны относительно оси ![]() , нечетные – относительно
начала координат, т.е. точки
, нечетные – относительно
начала координат, т.е. точки ![]() .
.
Четные функции – это ![]() .
Нечетные –
.
Нечетные – ![]() ,
, ![]() .
.
Полезно помнить, что если в аналитическое выражение функции входит произведение или частное четных и нечетных функций, то можно пользоваться правилом знаков, т.е. произведение (частное) одноименных (либо четных, либо нечетных) функций есть функция четная, разноименных – нечетная.
Поэтому функция  –
нечетная, т.к.
–
нечетная, т.к. ![]() нечетная,
нечетная, ![]() – четная,
– четная, 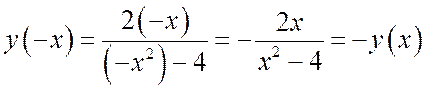 ,
и ее график симметричен относительно точки
,
и ее график симметричен относительно точки ![]() .
Аналогично
.
Аналогично  – нечетные функции.
– нечетные функции.
К сумме и разности это свойство неприменимо. Функции, не обладающие свойством симметрии, называют функциями общего вида.
Точки пресечения графика ![]() с
осями координат находятся из решения уравнений:
с
осями координат находятся из решения уравнений: ![]() –
точки пересечения с осью
–
точки пересечения с осью ![]() (их называют корнями),
(их называют корнями),
![]() – точки пересечения с осью
– точки пересечения с осью ![]() .
.
У нечетных функций точка ![]() является
и корнем и точкой пересечения с осью
является
и корнем и точкой пересечения с осью ![]() .
.
Для нашей
функции 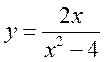 , если
, если ![]() ,
то
,
то ![]() , что и следовало ожидать, и других
точек пересечения с осями координат нет:
, что и следовало ожидать, и других
точек пересечения с осями координат нет: ![]() .
Поэтому ее график будет выглядеть так (рис. 14.2):
.
Поэтому ее график будет выглядеть так (рис. 14.2):
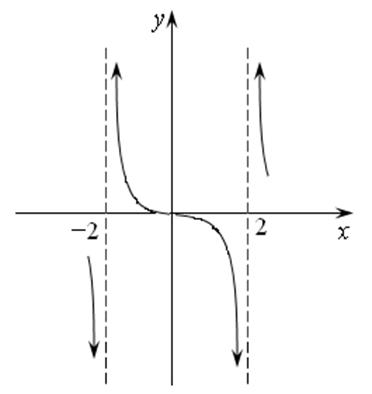
Рис. 14.2.
Отысканием корней вы много занимались в школе и мы рассказывали о методе половинного деления (см. лекцию 10), поэтому подробно на этом моменте останавливаться не будем.
Определение 14.1. Функция ![]() , непрерывная на интервале
, непрерывная на интервале ![]() называется возрастающей,
если большему значению аргумента
называется возрастающей,
если большему значению аргумента ![]() соответствует
большее значение
соответствует
большее значение ![]() , т. е. из
выполнения неравенства
, т. е. из
выполнения неравенства ![]() следует выполнение неравенства
следует выполнение неравенства
![]() .
.
Определение 14.2. Функция ![]() , непрерывная на интервале
, непрерывная на интервале ![]() называется убывающей,
если большему значению аргумента
называется убывающей,
если большему значению аргумента ![]() соответствует
меньшее значение
соответствует
меньшее значение ![]() , т. е. из
выполнения неравенства
, т. е. из
выполнения неравенства ![]() следует выполнение неравенства
следует выполнение неравенства
![]() .
.
Теорема 14.1 (необходимое условие возрастания
функции). Пусть функция ![]() дифференцируема на отрезке
дифференцируема на отрезке ![]() . Для того, чтобы она была всюду
возрастающей на этом отрезке необходимо, чтобы ее первая производная
. Для того, чтобы она была всюду
возрастающей на этом отрезке необходимо, чтобы ее первая производная ![]() была всюду неотрицательна, т.е.
была всюду неотрицательна, т.е. ![]() .
.
Доказательство.
Дано: ![]() – возрастает на
отрезке
– возрастает на
отрезке ![]() .
.
Доказать: ![]() (рис. 14.3).
(рис. 14.3).
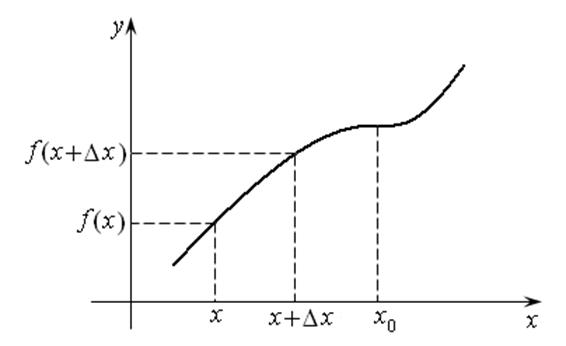
Рис. 14.3
1. Возьмем произвольную точку ![]() и
дадим аргументу положительное приращение
и
дадим аргументу положительное приращение ![]() .
Тогда
.
Тогда ![]() и
и ![]() по
условию.
по
условию.
2. Рассмотрим отношение приращения функции ![]() к вызвавшему его приращению
аргумента
к вызвавшему его приращению
аргумента ![]() :
:
 (нас интересует
знак).
(нас интересует
знак).
3. Найдем предел этого отношения при ![]() :
:
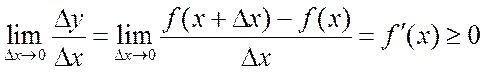 .
.
Откуда взялся знак равенства? Он возник в точках, где
приращение ![]() не просто стремиться к нулю, а равно
нулю при
не просто стремиться к нулю, а равно
нулю при ![]() , как в точке
, как в точке ![]() .
.
Таким образом, необходимое условие возрастания функции доказано. Сформулируем и докажем теперь достаточное условие возрастания функции.
Теорема 14.2 (достаточное условие возрастания
функции). Пусть функция ![]() дифференцируема на отрезке
дифференцируема на отрезке ![]() и ее производная
и ее производная ![]() всюду положительна, т.е.
всюду положительна, т.е. ![]() . Тогда функция
. Тогда функция ![]() будет всюду возрастающей.
будет всюду возрастающей.
Доказательство.
Дано: ![]() на отрезке
на отрезке ![]() .
.
Доказать: ![]() – возрастает на
этом интервале.
– возрастает на
этом интервале.
1. Возьмем две произвольные точки: ![]() и
и ![]() ,
где
,
где ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.