2. Рассмотрим разность ![]() .
Напишем для нее формулу Лагранжа (а вы думали, что мы о ней забудем до
экзамена?). Итак,
.
Напишем для нее формулу Лагранжа (а вы думали, что мы о ней забудем до
экзамена?). Итак, ![]() .
.
3. По условию ![]() ,
и
,
и ![]() по нашему выбору (см. п. 1), поэтому
произведение
по нашему выбору (см. п. 1), поэтому
произведение ![]() .
.
4. Но тогда и ![]() (левая
и правая части равенства всегда имеют одинаковые знаки), т. е.
(левая
и правая части равенства всегда имеют одинаковые знаки), т. е. ![]() , что и говорит о возрастании
, что и говорит о возрастании ![]() .
.
Таким образом, необходимое и достаточное условия возрастания функции нами полностью доказаны. Запишем формулировки рассмотренных теорем символически следующим образом:

Вопросы для размышления.
1. Являются ли теоремы 14.1 и 14.2 взаимно обратными? В чем между ними различие?
2. Как изменятся формулировки этих теорем, если мы будем рассматривать не строго возрастающие функции? Можно ли их объединить в одну теорему?
Аналогично доказываются необходимое и достаточное условия убывания функции.
Теорема 14.3 (необходимое условие убывания функции). Пусть функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() . Для того, чтобы она была всюду убывающей
на этом отрезке необходимо, чтобы ее первая производная
. Для того, чтобы она была всюду убывающей
на этом отрезке необходимо, чтобы ее первая производная ![]() была
всюду неположительна, т.е.
была
всюду неположительна, т.е. ![]() .
.
Теорема 14.4 (достаточное условие убывания функции). Пусть функция ![]() дифференцируема
на отрезке
дифференцируема
на отрезке ![]() и ее производная
и ее производная ![]() всюду отрицательна, т.е.
всюду отрицательна, т.е. ![]() . Тогда функция
. Тогда функция ![]() будет всюду убывающей.
будет всюду убывающей.
Символически это записать следующим образом:
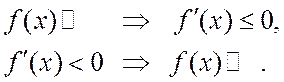
Напомним, что функция только возрастающая или только убывающая называются монотонными и термин «интервалы возрастания - убывания» – заменятся термином «интервал монотонности».
А теперь, вооруженные признаками для определения интервалов монотонности, а также теоремой Ферма для экстремумов, дадим признаки существования максимума и минимума функции для практического их применения.
Определение 14.3. Точки, отделяющие интервал возрастания непрерывной функции от интервала убывания (или наоборот) называются экстремумами функции.
В зависимости от того, какие интервалы (возрастания или убывания) находятся слева и справа от экстремальной точки, их называют точками локального максимума или минимума, потому что значение функции в этих точках будут наибольшими или наименьшими только для некоторой их окрестности. Экстремальные точки всегда интересны, ведь они являются точками наивысшего подъема или падения, пусть даже и местного значения.
По теореме Ферма, рассмотренной в лекции 13,
производная в этих точках равна нулю, либо не существует. Но как показывают
контрпримеры, например функции для ![]() равенство нулю
производной в точке
равенство нулю
производной в точке ![]() не гарантирует наличия
экстремума – обратная теорема не всегда верна. И смотреть значения функции
слева и справа от экстремумов тоже задача хоть и интересная, но иногда
затруднительная. Например, как найти значения функции
не гарантирует наличия
экстремума – обратная теорема не всегда верна. И смотреть значения функции
слева и справа от экстремумов тоже задача хоть и интересная, но иногда
затруднительная. Например, как найти значения функции ![]() и
др. функций, не имея под рукой хорошего калькулятора? Поэтому для нахождения
точек экстремумов воспользуемся определением 14.3 и найдем простые, гарантированные
признаки, позволяющие определять, как будет вести себя функция вблизи минимума
или максимума – возрастать или убывать.
и
др. функций, не имея под рукой хорошего калькулятора? Поэтому для нахождения
точек экстремумов воспользуемся определением 14.3 и найдем простые, гарантированные
признаки, позволяющие определять, как будет вести себя функция вблизи минимума
или максимума – возрастать или убывать.
Теорема 14.5 (необходимое и достаточные условия
максимума). Пусть функция ![]() дифференцируема на отрезке
дифференцируема на отрезке ![]() . Для того, чтобы функция в точке
. Для того, чтобы функция в точке ![]() функция имела максимум необходимо,
чтобы производная в этой точке равнялась
функция имела максимум необходимо,
чтобы производная в этой точке равнялась ![]() (или
не существовала) и достаточно, чтобы
(или
не существовала) и достаточно, чтобы ![]() меняла свой знак
с (+) на (–) при переходе через
меняла свой знак
с (+) на (–) при переходе через ![]() слева направо.
слева направо.
Необходимость следует из теоремы Ферма. Если ![]() – точка максимума, то
– точка максимума, то ![]() (или не существует).
(или не существует).
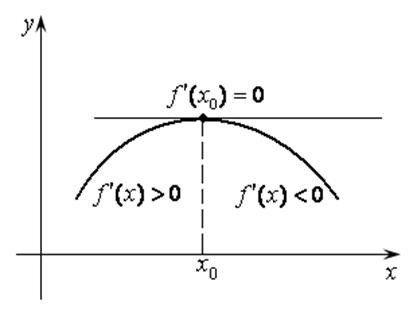
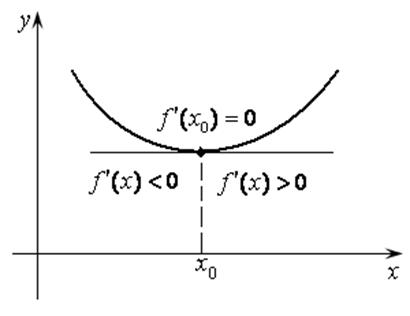
Рис. 14.4 Рис. 14.5
Достаточность диктуется определением максимума, как
точки, отделяющей интервал возрастания от интервала убывания. Слева от ![]() функция возрастает, следовательно,
ее производная
функция возрастает, следовательно,
ее производная ![]() ; справа убывает и
; справа убывает и ![]() , т. е. меняет свой знак в точке
, т. е. меняет свой знак в точке ![]() . Значит в точке
. Значит в точке ![]() функция имеет максимум.
функция имеет максимум.
Аналогично вводится признак существования минимума функции.
Теорема 14.6 (необходимое и достаточные условия минимума). Пусть функция ![]() дифференцируема
на отрезке
дифференцируема
на отрезке ![]() . Для того, чтобы функция в точке
. Для того, чтобы функция в точке ![]() функция имела минимум необходимо,
чтобы производная в этой точке равнялась
функция имела минимум необходимо,
чтобы производная в этой точке равнялась ![]() и
достаточно, чтобы
и
достаточно, чтобы ![]() меняла свой знак с (–) на
(+) при переходе через
меняла свой знак с (–) на
(+) при переходе через ![]() слева направо (рис.
14.5).
слева направо (рис.
14.5).
Таким образом, порядок действия нахождения экстремумов функции таков:
1. Находим ![]() и решаем
уравнение
и решаем
уравнение ![]() . К корням этого уравнения добавляем
точки, в которых производная не существует. Все эти точки являются точками
подозрительными на экстремум (критические точки).
. К корням этого уравнения добавляем
точки, в которых производная не существует. Все эти точки являются точками
подозрительными на экстремум (критические точки).
2. Определяем знаки ![]() вблизи
критических точек на всех интервалах непрерывности.
вблизи
критических точек на всех интервалах непрерывности.
3. Делаем выводы о наличии экстремумов и интервалов возрастания и убывания.
4. Находим ординаты экстремальных точек ![]() , где
, где ![]() –
экстремум.
–
экстремум.
Обычно все значения знаков ![]() сводятся
в таблицу (школьный прием) и делаются соответствующие выводы. Не будем ломать
стереотип. Добавим только, что исследования необходимо проводить на всех
интервалах непрерывности.
сводятся
в таблицу (школьный прием) и делаются соответствующие выводы. Не будем ломать
стереотип. Добавим только, что исследования необходимо проводить на всех
интервалах непрерывности.
Пример 14.1. Определить экстремумы функций:
1) 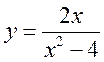 , 2)
, 2) 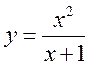 .
.
Решение.
1) С первой функцией мы уже знакомы и знаем, что ее ОДЗ являются интервалы ![]() . Найдем
. Найдем
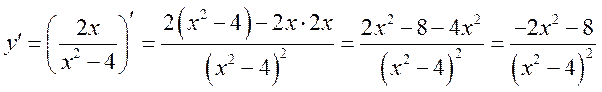 .
.
а) ![]() , т. к.
, т. к. ![]() ,
поэтому экстремумов нет.
,
поэтому экстремумов нет. ![]()
б) определим
знак ![]() на каждом из интервалов. Поскольку
на каждом из интервалов. Поскольку ![]() для любых
для любых ![]() ,
то знак
,
то знак ![]() будет всегда отрицательным. То есть
на всех интервалах непрерывности наша функция будет убывать, что и
демонстрирует рис. 14.2.
будет всегда отрицательным. То есть
на всех интервалах непрерывности наша функция будет убывать, что и
демонстрирует рис. 14.2.
2) Исследуем
вторую функцию по плану.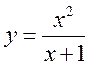 ,
, ![]() .
.
а) 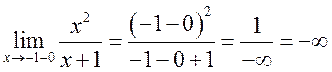 ,
, 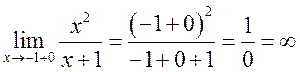 .
.
б) Функция
общего вида, т.к. 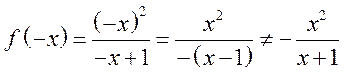 .
.
в) корни
функции: ![]() , если
, если ![]() ,
т.е.
,
т.е. ![]() – корень. Точки пересечения с осью OY:
– корень. Точки пересечения с осью OY: ![]() точка
точка ![]() .
.
г) 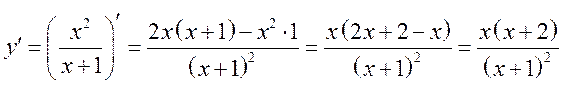 .
.
![]() , если
, если ![]() и
и
![]() , т.е.
, т.е. ![]() .
.
Составим
таблицу знаков ![]() .
.
|
x |
|
Вывод |
|
|
|
+ |
возрастает |
|
|
–2 |
0 |
максимум |
|
|
|
– |
убывает |
|
|
|
– |
убывает |
|
|
0 |
0 |
минимум |
|
|
|
+ |
возрастает |
Строим схематичный график (рис. 14.6.).
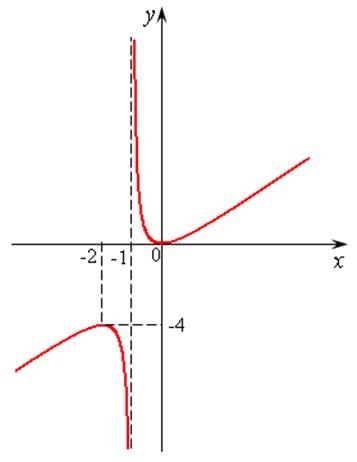
Рис. 14.6
Вот видите, здесь максимальная точка ниже минимальной, поэтому их и не называют наибольшим и наименьшим значениями функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.