Теоремы о дифференцируемых функциях. Исследование поведения функции. Приложения производных к экономическим задачам. Функции многих переменных, страница 14

2. Определение коэффициентов выбранной зависимости, чтобы она в каком-то смысле наилучшим образом описывала рассматриваемый процесс.

Для решения второй задачи разработаны различные методы корреляционного и дисперсионного анализа, в основе которых лежат два требования, предъявляемых к выбранной функции:

3. Сумма отклонений эмпирических данных от расчетных должна быть равна нулю:

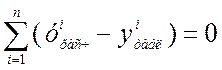.                                             (17.2)

Это требование было необходимым, но недостаточным для того, чтобы определить коэффициенты искомой функции. Поэтому выдвинули второе требование

4. Сумма квадратов отклонений эмпирических данных от расчетных должна быть наименьшей:

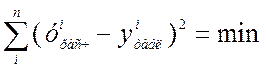.                                        (17.3)

Отсюда название метода – метод наименьших квадратов. Покажем его действие на примере.

Пусть в результате эксперимента получено nзначений функции у при соответствующих значения х. Результаты записаны в таблицу.

Таблица 17.1

			…
			…

Требуется построить кривую, наилучшим образом описывающую эти данные. Она может быть любого вида – прямая, гипербола и т.д. Остановимся на простейшем – прямой, уравнение которой запишем в виде .

Рассмотрим сумму квадратов разностей значений по формуле (17.2):

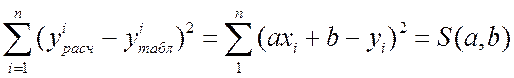.                   (17.3)

Подберем параметры а и bтак, чтобы эта сумма имела наименьшее значение – то есть решим задачу из п. 17.3. На основании теоремы 17.1 следует, что частные производные функции S(a,b) по параметрам а и b  должны быть равны нулю. Учтем, что функция S(a,b) сложная, поэтому сначала берем производную от квадрата, а потом от суммы:

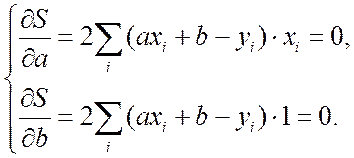                              (17.4)

Сократим оба уравнения на 2 и запишем их в виде системы уравнений.

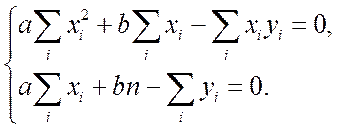                                (17.5)

Эта система всегда имеет решение. Для удобства ее решения в таблицу опытных данных добавим столбцы  , , а также строку для записи соответствующих сумм.

Пример 17.7. В результате опыта получены следующие данные:

№
1	0,25	2,57	0,6425	0,0625	0,0049
2	0,37	2,31	0,8547	0,1369	–0,0116
3	0,44	2,12	0,9328	0,1936	0,0171
4	0,55	1,92	1,0560	0,3025	–0,0362
5	0,60	1,75	1,050	0,3600	0,0186
6	0,62	1,71	1,0602	0,3844	0,0125
7	0,68	1,60	1,088	0,4624	–0,0157
8	0,70	1,51	1,0570	0,4900	0,0282
9	0,73	1,50	1,0950	0,5329	–0,0237
10	0,75	1,41	1,0575	0,5625	0,013
Сумма	5,69	18,4	9,8937	3,4877	0,0001

Для нахождения коэффициентов а и b подставим в систему (17.5) найденные значения сумм и получим следующее:

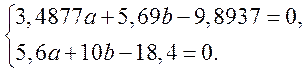
Решим ее любым способом и найдем значения

а = –2,3038 и b = 3,1508.

Таким образом, искомое уравнение связи между у и х будет иметь вид

.

Построим полученную прямую (рис. 17.5).

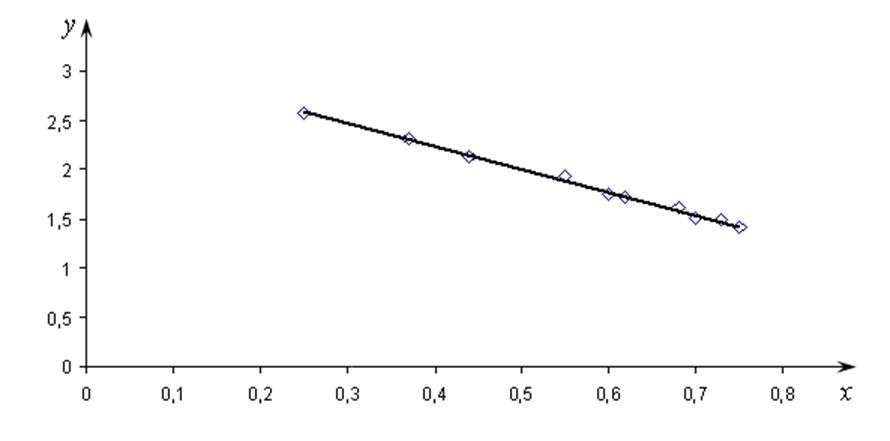
Рис. 17.5

Для проверки правильности подобранных коэффициентов составляем  разности между расчетными и табличными значениями у. Покажем, как это делается.

Если х = 0,25, то

,     .

Если х = 0,37, то

,   

и т.д.

Суммарная ошибка отлична от нуля в четвертом знаке после запятой, а исходные данные имели два знака, поэтому в условиях нашего опыта можно считать, что ошибка приближения практически равна нулю.

Если за аппроксимирующую функцию взят трехчлен второй степени

,                                          (17.6)

то выражение (17.3) запишется в виде

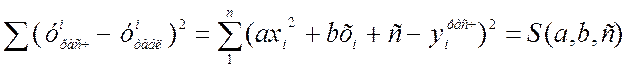,        (17.7)

а соответствующая система (17.4) будет иметь три уравнения с тремя неизвестными a,b,c

Сейчас подбор вида и коэффициентов соответствующей функциональной зависимости можно осуществить на компьютере. В основе практически всех программ и «Exсel» и «Статистика» лежит проверенный метод наименьших квадратов.

На этом мы заканчиваем тему «Функции многих переменных». Последняя лекция проиллюстрировала всеобщий закон развития: количество рождает новое качество. Две независимые переменные привели две частных производных первого порядка  и четыре – второго. Появились чистые и смешанные производные высших порядков, производная по направлению и градиент. К привычным со школы минимуму и максимуму присоединился минимакс. О, сколько нам открытий чудных …. И это – правда. Готовит.

Счастливой сдачи экзамена по высшей математике!  

ЛИТЕРАТУРА

1. Высшая математика для экономистов. /Под ред. Н.Ш. Кремера. М: ЮНИТИ, 2002.

2. Красс М.С. Математика для экономических специальностей. М: ИНФРА-М, 1999.

3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. В 2-х ч. М: Финансы и статистика, 2000.

4. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1,2.- Спб.: Мифрил, 1996.

5. Шипачев В.С. Высшая математика. М: Высш. шк., 1998.

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М: Высш. шк., 1996.

7. Гусак А.А. Высшая математика. В 2-х т.: Учеб. пособие. Мн: ТетраСистемс, 1998.

ПРИЛОЖЕНИЕ

Поверхности второго порядка

Поверхность		Уравнение
1. Эллипсоид
2. Гиперболоид
а) Однополостной
б) Двуполостной
3. Параболоид
а) Эллиптический
б) Гиперболический
4. Конус
5. Цилиндр
а) Эллиптический
б) Гиперболический
в) Параболический