Теоремы о дифференцируемых функциях. Исследование поведения функции. Приложения производных к экономическим задачам. Функции многих переменных, страница 2

Формула (13.1) иногда записывается в следующем виде:

                                  (13.5)

и читают так: приращение  функции на отрезке  равно произведению длины этого отрезка  на значение производной от этой функции в некоторой внутренней точке   –  .

Аналог этой формулы мы встретим и в интегральном исчислении, когда будем знакомиться со свойствами определенного интеграла

.

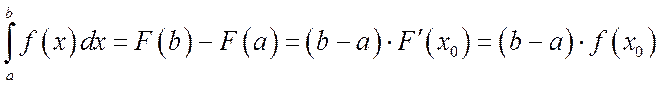Подобные формулы существуют и в двойных и в тройных интегралах. Их называют теоремами о среднем значении. О каком же «среднем» значении идет речь в теореме Лагранжа?

Вспомним механический смысл производной. Если  – путь, пройденный точкой от начального положения, то  есть путь, пройденный с момента  по момент , а отношение  – средняя скорость за этот промежуток времени. Причем неважно, какие зигзаги делал этот путь – важны начальная  и конечная  точки. Поэтому и  – это скорость в серединной (или очень близкой к ней) точке отрезка . Интересный результат, правда? Мы его потом используем в экономике.

Пример 13.2. На кривой  найти точку, в которой скорость изменения имеет среднее значение на отрезке .

Решение. Запишем формулу Лагранжа с учетом, что  и .

,

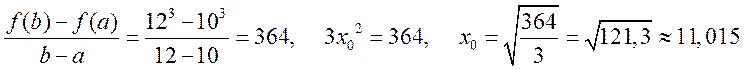т.е. близко к середине отрезка . Число 364 – это скорость. Она может измеряться в км/ч, если x измеряется в часах, y в километрах; руб./мес., если y – это деньги, x – время в месяцах и т.д.

Следующая теорема является обобщением теоремы Лагранжа на случай двух функций  и . Она позволяет сравнивать скорости изменения этих функций на отрезке  с результатами приращений. Интуитивно ясно, чем больше приращение, тем больше скорость. Именно об этом говорит теорема Коши.

13.5. Теорема Коши об отношении приращений

Теорема 13.4 (теорема Коши). Если функции  и  непрерывны и дифференцируемы на отрезке , причем  и , то внутри этого отрезка найдется хотя бы одна точка , для которой выполняется равенство:

.                                      (13.6)

То есть пути, пройденные функциями  и  в промежуток  относятся как скорости в какой-то промежуточной точке , одинаковой для обеих функций.

Доказательство. Доказывают эту теорему с помощью введения вспомогательной функции

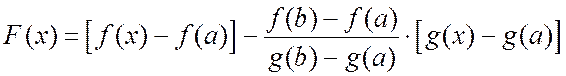,                    (13.7)

которая отвечает теореме Ролля:  (проверьте, вместо  подставив  и ), непрерывна и дифференцируема, как и  и , поэтому найдется хотя бы одна точка , в которой .

Находим  для равенства (13.7):

как производные от постоянных. Откуда и получаем формулу (13.6).

Должны сказать, что доказательств всех четырех вышеизложенных теорем существует множество, поэтому мы не стали приводить их здесь, в этом пособии. Найдите их в учебнике, придумайте свое – выбор за вами, но результат должен быть.

А теперь вопрос: можно ли было доказать теорему Коши с помощью простого деления левой части (и числителя и знаменателя) на , вот так:

?

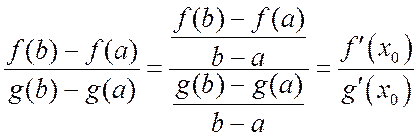Та ли это точка , о которой шла речь в теореме Лагранжа (приблизительно середина отрезка )? Подумайте. А пока пример.

Пример 13.3. Две фирмы в течении двух лет , получали прибыль по законам: первая , вторая . Во сколько k раз вторая фирма получит больше прибыли на конец 2 года и в какой промежуток времени скорости их обогащения будут также равны k?

Решение.

а) Найдем приращение прибылей для каждой фирмы:

I.   ,

II.   .

б) Найдем число k:

.

Следовательно вторая фирма получит в 2 раза больше прибыли, чем первая.

в) Найдем отношение скоростей  обогащения и точку, в которой .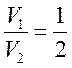

,   ,   .

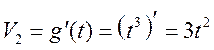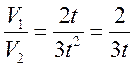По условию 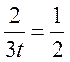, откуда . То есть в момент времени  года скорости их обогащения будут равны .

Ну и, наконец, еще одна теорема, которая имеет практическое приложения для вычисления различных пределов.

13.6. Правило Лопиталя. Раскрытие неопределенностей

Теорема 13.5 (правило Лопиталя). Пусть функции  и  – бесконечно малые величины при () и их отношение дает неопределенность 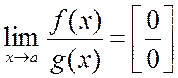. Если существует предел отношения производных этих функций 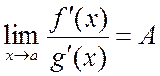, то к такому же пределу будет стремиться и отношение 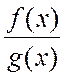, т.е.

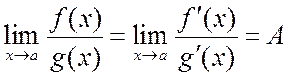.                                       (13.8)

Если 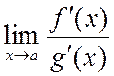 – так же даст неопределенность 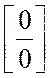, то к нему можно применить правило Лопиталя еще раз.

Обращаем ваше внимание, что в формуле (13.8) присутствует именно частное производных, а не производная частного.

Доказывается эта теорема с помощью теоремы Коши для отрезка .

Правило Лопиталя можно использовать и в случае неопределенностей типа . Главное, на каждом этапе проверять имеем ли мы еще неопределенности указанных видов или нет, т.к. 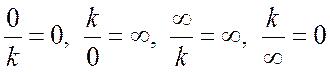, если  – число и к этим выражениям применять правило Лопиталя нельзя.

Примеры 13.4. Вычислить пределы, используя правило Лопиталя.

1. .

2. .

В данном примере мы дважды использовали правило Лопиталя.

3. .

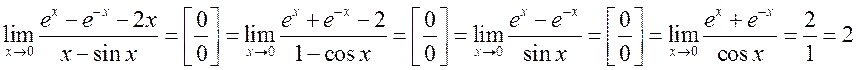Применение правила Лопиталя можно комбинировать с преобразованиями и прямой подстановкой предельных значений к части подпредельного выражения.

4. .

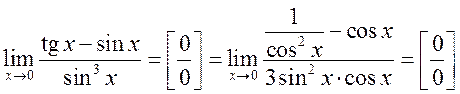Преобразуем выражение 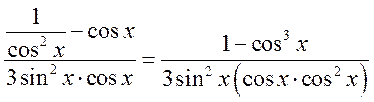. Учтем, что  и тогда под знаком предела останется выражение 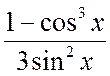. Применим к нему правило Лопиталя:

.

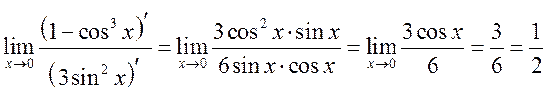5. .

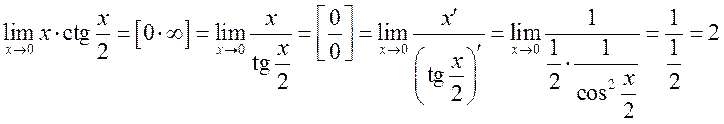Можно ли применить правило Лопиталя к неопределенностям вида . Да, можно, но предварительно выражение нужно прологарифмировать.

6. .

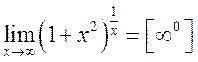Предположим, что предел этого выражения существует и равен А, то есть 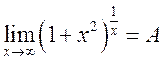. Прологарифмируем обе части равенства.

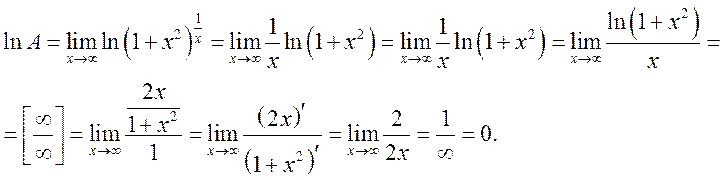
Сведем начало и конец воедино.

, то есть .

Лекция 14.

ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИИ

Следует помнить, что в каком-то смысле высшая математика проще элементарной. Исследовать, например, лесную чащу пешком очень трудно, а с самолета это делается проще.

У. Сойер
(английский математик и педагог)

ПЛАН

1.  Введение.

2.  Область определения функции.

3.  Симметрия, точки пересечения с осями координат.

4.  Интервалы возрастания и убывания функции.

5.  Точки экстремума. Необходимые и достаточные условия.

6.  Введение. Общий план исследования функции.

7.  Выпуклость и вогнутость формы графика. Точки перегиба.

8.  Асимптоты функции.

9.  Пример исследования функции.

10. Заключение.

14.1. Введение