Анализ и синтез передаточных элементов в технических системах, страница 2

Деформации бывают: упругие и остаточные.

Упругие – исчезают после снятия внешней нагрузки, а остаточные – сохраняются.

Механическое напряжение – это мера действия сил упругости (Па=Н/м2).

Напряжение бывает 2-х видов: нормальное – направлено перпендикулярно площади поперечного сечения  d (сигма), и касательное – лежащие в плоскости поперечного сечения, т.е. направленное по касательной  t (тау).

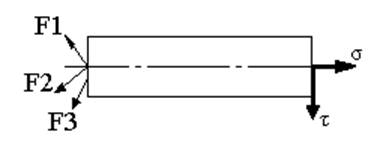
По характеру воздействия на деталь может возникать следующее напряжения (деформации): растяжение, сжатие, смятие, изгиб (d), сдвиг, срез, кручение (t), или сочетания этих деформаций.

В зависимости от материала для каждой детали существует опасное напряжение.  Механические свойства материала определяются графической зависимостью напряжения от относительного удлинения при испытании образца на растяжение.

Диаграмма растяжения образца:

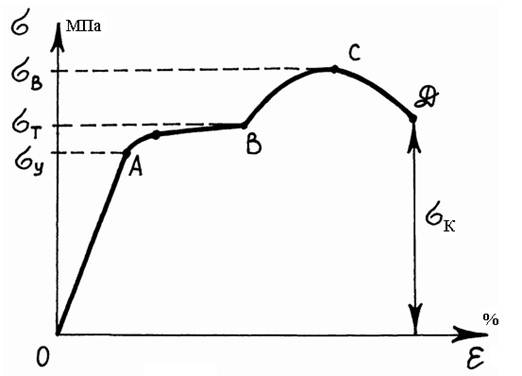
Закон ГУКА:напряжение прямо пропорционально относительному удлинению.

  ,

где   E – модуль упругости материала (величина табличная),

 - относительное удлинение в %

На участке ОА соблюдается линейная зависимость, т.е. выполняется закон ГУКА. Напряжение, возникающее в точке А  называется _у предел упругости. Это напряжение допускает 0.05% остаточной деформации.

На участке АВ удлинение растет интенсивнее, чем приложение силы. Материал тускнеет (течет). Этот участок называется площадкой текучести. _Т(предел текучести)=0.2% от остаточной деформации.

На участке ВС материал вновь начинает сопротивляться приложению силы, но не подчиняется линейному закону. Напряжение в точке С обозначается _в и называется временное сопротивление. Один и тот же материал на этом участке ведет себя по-разному.

На участке СД для удлинения образца требуется уже меньшее приложение силы, т.е. материал перестает сопротивляться.  В точке Д происходит разрыв _к-конечное напряжение.

Для пластичных материалов считается опасным предел текучести _Т (0,2%),

_опасн=_Т.

В расчетах деталей механизмов на прочность используют допускаемые напряжения, которые составляют часть от опасного и гарантируют надежность работы детали в течение заданного срока эксплуатации.

Допускаемое напряжение всегда пишется в [] – в скобках.

Допускаемое напряжение при растяжении находится:

[_р]= _т/n

n – коэффициент запаса прочности. Зависит от условий работы детали, ее ответственности, методов расчета и других факторов. n>=1

n=1 применяется только в авиационной техники и ракетостроении.

Принято считать что любое нормальное напряжение , кроме растяжения связано зависимостью []≈2[_р]

Любое допускаемое касательное напряжение [_Т ]≈ 0.5[_р]

При расчете на прочность обязательно должно выполняться условие прочности:

Максимальные действительные напряжения (расчетные) не должны превышать допускаемых значений напряжений

_max<=[]          и      _max<=[].

5.               Теории прочности при расчете деталей машин.

В зависимости от прочностных характеристик материалов, оценивают возможность разрушения материала или переходов состояния текучести на основании гипотез о том, какой фактор вызовет появление опасного состояния.

Существуют 4 теории прочности.

1)  Теория максимальных опасных напряжений:

При достижении действительными напряжениями предела текучести возникают опасные напряжения. 

     _max<=[] ,     _max<=[]

2)  Теория наибольших относительных деформаций.

Опасное состояние возникает, когда наибольшее относительное удлинение достигает определенного значения.

3)  Теория наибольших касательных напряжений (при сложных деформациях).

Опасное состояние возникает, когда в детали присутствуют касательные напряжения, превышающие в 2 раза нормальные.

=<=[]

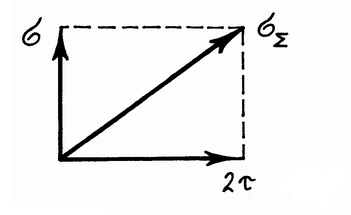
4)  Энергетическая теория прочности.

С учетом удельной потенциальной энергии изменения формы деталей возникает опасное состояние при достижении значения касательных напряжений, превышающих в 1.7 раза нормальное.

=<=[]

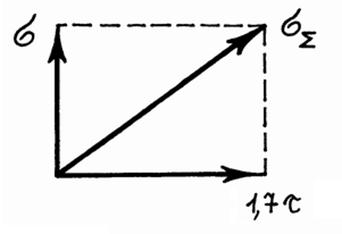
Расчет деталей по коэффициенту запаса прочности.

После расчета деталей на прочность по допускаемым напряжениям проводят расчет на надежность по коэффициенту запаса по прочности. Расчетный коэффициент запаса прочности должен превышать допускаемое значение. n>=[n], где [n] зависит от вида детали, применения и материала.

При одноименных напряжениях, действующих на деталь, соответственно рассчитывают коэффициент запаса прочности по нормальным напряжениям n или по касательным напряжениям

При этом учитывается материал, из которого изготовлена деталь, влияние концентрации напряжений и цикличность нагрузки.

При разноименных напряжениях общий коэффициент запаса прочности находят из зависимости:

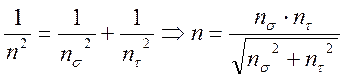>=[n].

 

 

 (1.10.04)     Геометрические характеристики плоских поперечных сечений

При равномерном распределенном напряжении по сечению геометрической характеристикой является площадь поперечного сечения (при деформациях: растяжениях, сжатиях, смятиях, сдвиге, срезе), при неравномерном распределении напряжений геометрическими характеристиками являются осевой момент инерции и осевой момент сопротивления (при деформации изгиба) полярный момент инерции и полярный момент сопротивления (при деформации кручения).