Помехи в линейных трактах и каналах многоканальных систем передачи с ЧРК, страница 9

Комбинационные продукты нелинейности с частотами (ƒ_x + ƒ_y   - ƒ_z ),  называются продуктами 1-го рода. Заметим, что признаком  продуктов нелинейности 1-го рода с частотами ( mƒ_xnƒ_{y  q}ƒ_{z …})  является равенство m±n±q±...=1.                                                                                  (3.56)

 Продукты нелинейности 3-го порядка 1- го рода с частотой F=ƒ_x + ƒ_y   - ƒ_z можно рассматривать как результат взаимодействия суммарных продуктов нелинейности 2- го рода с частотами ƒ_n = ƒ_x + ƒ_y   и спектральных составляющих группового сигнала с  частотами (ƒ_n-F) .Мощность этих продуктов с частотой F определится площадью пересекающихся областей функций P(ƒ_n) и P(F+ ƒ_z). Функция P(ƒ_n) определяется выражением (3.47) и в соответствии с рис, 3.19 2ƒ₁ ƒ_n 2ƒ₂ .

    В свою очередь, минимальное и максимальное значения частоты (F+ ƒ_z) равны соответственно(F+ ƒ₁) и (F+ ƒ₂).При  F= ƒ₁ и  F= ƒ₂  взаимное расположение спектров функций Р(ƒ_n) и Р(F+ ƒ_z) показано на рис. 3.24, а. Площади пересекающихся областей  этих функций в данном случае равны. На рис. 3.24, б показано взаимное расположение спектров функций Р(ƒ_n) и Р(F+ ƒ_z) соответствующих максимальной площади их пересекающихся областей, а значит, и максимальной мощности продуктов нелинейности 3-го порядка 1-го рода с частотой F.

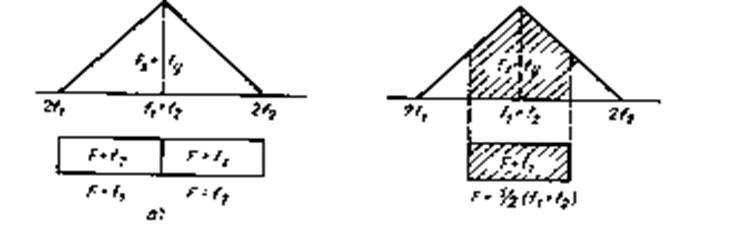
           а)                                                             б)

Рис. 3.24. Взаимное расположение спектров функций Р(ƒ_n) и Р(F+ ƒ_z)

                                                    при:

                              а- F= ƒ₁  и F= ƒ₂ ; б- F=0,5(ƒ₁+ ƒ₂)

 При этом F=0,5(ƒ₁+ ƒ₂).   Аналогичные рассуждения позволяют определить характер изменения мощности продуктов нелинейности 3-го порядка с частотами F= ƒ_x + ƒ_y  + ƒ_z называемыми продуктами 2-го рода. Общая мощность продуктов нелинейности 3-го порядка с частотой F может быть получена в виде

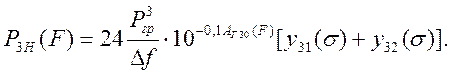                                           (3.57)

Здесь и - нормированные функции спектрального распределения мощности продуктов нелинейности 3-го порядка 1-го и 2-го родов соответственно. Нормированную частоту  можно найти по формуле (3.54), а функции и по формулам

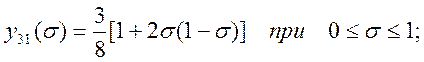                                                     (3.58)

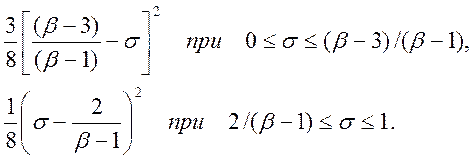   =                       (3.59)

    Заметим, что функция  зависит от относительной ширины линейного спектра СП, а значение функции с увеличением  возрастает (рис. 3.25).

    В спектре одного канала передачи, ширина полосы частот которого ,спектральную плотность продуктов нелинейности можно считать равномерной. При этом условии псофометрическая мощность (пВт псоф) нелинейных помех в канале передачисо средней частотой F в ТНОУ на выходе усилителя с учетом (3.51) и (3.57) определяется в виде:

    для помех 2-го порядка:

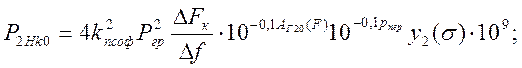                                     (3.60)

    для помех 3-го порядка

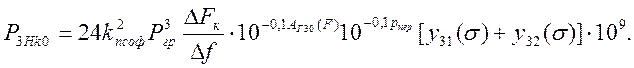                     (3.61)

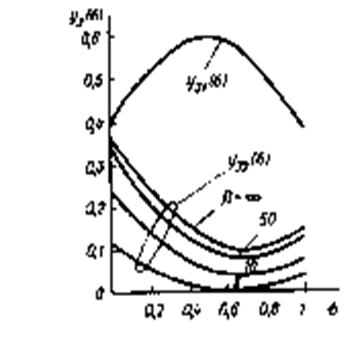
Рис. 3.25. Зависимость функции спектраль-

ного распределения мощности продуктов

нелинейности 3-го порядка 1-го и 2-

го  рода от нормированной частоты

и относительной ширины линейного спект-

ра

Здесь р_пер относительный уровень передачи на выходе усилителя в спектре канала ТЧ.

     При работе СП с перекосом уровней происходит перераспределение мощностей нелинейных помех по спектру. В частности, увеличение уровня частотных составляющих группового сигнала

в верхней части линейного спектра, вызванное введением предыскажения, приводит к увеличению мощности разностных продуктов нелинейности, вызванных взаимодействием этих составляющих. Последние попадают в нижние по спектру каналы СП, где мощность нелинейных помех увеличивается. Соответст-

венно с уменьшением уровня частотных составляющих группового сигнала в нижней части линейного спектра уменьшается мощность суммарных продуктов нелинейности, вызывающих нелинейные помехи в верхних по спектру каналах СГ. Для расчета мощности нелинейных помех в канале передачи в выражениях

(3.60) и (3.61) используются нормированные функции спектральной плотности у_2п() и у_3п() рассчитываемые по формулам, учитывающим введение перекоса уровней. При линейном предыскажении уровней с величиной перекоса р.

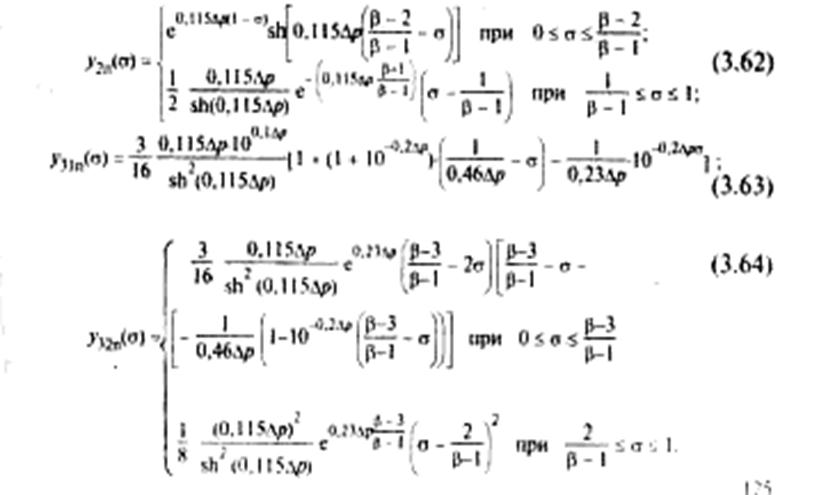
В [4] приведены таблицы коэффициентов спектрального распределения нелинейных помех 2-го и 3-го порядков, рассчитанных по формулам (3.62) и (3.63).

Из (3.60) и (3.61) следует, что мощность нелинейных помех в канале передачи зависит от мощности группового (многоканального)сигнала, которая, в свою очередь, определяется статистическими характеристиками этого сигнала.

Гупповой сигнал и его статистические характеристики

    Групповой сигнал представляет собой совокупность канальных сигналов, передаваемых в групповом тракте. Канальные сигналы относятся к классу нестационарных процессов, которые можно рассматривать в виде совокупности частичных стационарных процессов. В телефонном канале, например, частичными

сигналами являются разговорные токи отдельных пар абонентов на активных участках разговора. При передаче вещательных программ в качестве частичных сигналов можно рассматривать разные по характеру отрывки программ – речь, пение, симфоническую музыку и т.д. Таким образом, канальные сигналы, образующие групповой сигнал, определяются совокупностью характеристик частичных сигналов с указанием относительного времени занятия канала этими сигналами.

    Многоканальный (групповой) сигнал как сумма канальных сигналов также является нестационарным случайным процессом, приводимым к случайной последовательности частичных стационарных процессов и обладающим эргодическим свойством. В соответствии с этим свойством статистические характеристики, полученные усреднением по множеству реализаций случайного процесса, с вероятностыо, сколь угодно близкой к единице, совпадают с характеристиками, полученными усреднением одной реализации за достаточно большой промежуток времени. Наиболее важными статистическими характеристиками группового сигнала являются его среднее значение, дисперсия и закон распре-