Помехи в линейных трактах и каналах многоканальных систем передачи с ЧРК, страница 7

    Характер распределения составляющих спектра входного группового сигнала зависит от места включения корректирующих устройств в усилителе и наличия предыскажения уровней.

    Для определения мощностей продуктов нелинейности на выходе усилителя используем упрощенный метод, основанный на представлении входящего сигнала суммой гармонических колебаний.

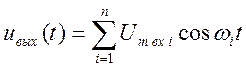                                                                (3.38)

Начальные фазы этих колебаний без потери общности рассуждений можно считать равными нулю. Подставив значение входного сигнала (3.38)] в полином (3.37) и используя известные алгебраические и тригонометрические формулы, находим частоты и амплитуды напряжений составляющих выходного сигнала, которые приведены в табл. 3.3.

При нахождении указанных величин учитывалось, что для квазилинейного   участка   АХ   справедливы   неравенства b₁>>b₂u_вх >>b₃u²_вх .Вследствие этого первые гармоники частотных составляющих входного сигнала на выходе усилителя определяются только из 1-гo члена полинома (3.37), продукты нелиней-

ности 2- гo порядка - из 2- гo члена полинома и т. д. В табл. 3.3 f_x , f_y , f_z –любая из частот составляющих входного группового сигнала, описываемого (3.38), а -амплитуды напряжений колебаний с этими частотами на выходе усилителя.

    При определении мощностей продуктов нелинейности, значения которых также приведены в табл. 3.3, произведен переход от амплитудных к действующим значениям напряжений и учтено сопротивление нагрузки на выходе усилителя.

    Для количественной оценки нелинейных свойств усилителей используют затухания нелинейности по второй (А_г2) и третьей (А_г3) гармоникам. По определению,

            ;                          (3.39)

                                          (3.40)

Здесь р_х, р_2Г, р_3Г  - уровни первых, вторых и третьих гармоник по напряжению или мощности на выходе усилителя. Подставляя и (3.39) и (3.40) значения мощностей вторых и третьих гармоник из табл. 3.3, находим

                                      А_Г2=А_Г20-р                                                      (3.41)

                                       А_Г3=А_Г30-2р                                                     (3.42)

Здесь под  мВт) понимается уровень мощности выходного сигнала при подаче на вход усилителя синусоидального сигнала с частотой f_x. Этот уровень при работе на квазилинейном участке АХ усилителя практически совпадает с уровнем первой  гармоники  выходного  сигнала  с  частотой f_x;

и -затухания по второй и третьей гармоникам соответственно при нулевом относительном уровне на выходе усилителя. С учетом полученных соотношений и данных табл. 3.3 можно выражение для мощностей продуктов нелинейности записать в виде:

                                         а)  

                                          б)   

                                         в)                                      (3.43)

                                          г)

                                         д)

Количество продуктов нелинейности определяется путем подсчета числа сочетаний из п элементов по т:

                                                 

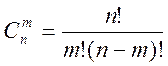
    Для продуктов 2-го порядка т = 2, а 3-го порядка т = 3

Общее число продуктов нелинейности при п >> 1 приведено в табл. 3.3. Данные этой таблицы и соотношения (3.43) показывают, что при Р_x = Р_y = Р_z =Р₀ ,т. е. при работе СП без перекоса уровней, мощности и количество комбинационных продуктов нелинейности значительно больше соответствующих величин

гармонических составляющих, которыми поэтому можно пренебречь. Практически следует учитывать только продукты нелинейности 2-го порядка с частотами ( f_x ± f_y ) и общей мощностью

                                                                          (3.44)

и продукты нелинейности 3-го порядка с частотами (f_x ± f_y ± f_z ) и общей мощностью

                                                                         (3.45)

Следует иметь в виду, что затухания нелинейности по гармоникам усилителя, охваченного цепью частотно-зависимой ОС, зависят от частоты. Поэтому в (3.43) надо подставлять значения А_Г20  и А_Г30 на частотах рассматриваемых продуктов нелинейности, а выражения (3.44) и (3.45) справедливы лишь при отсутствии частотно-зависимой ОС.

Спектральное распределение продуктов нелинейности

    Для определения мощности нелинейных помех, попадающих в канал передачи, необходимо знать спектральное распределение продуктов нелинейности, т. е. мощность этих продуктов в узкой полосе частот со средней частотой F. 

    При работе СП без перекоса уровней групповой сигнал на выходе усилителя имеет сплошной и равномерный спектр от f₁ до f₂   (рис. 3.16). Мощность группового сигнала в данном диапазоне частот

                                 ,                                      (3.46)

а за его пределами равна нулю. Здесь Р₀ - мощность сигнала на выходе усилителя в полосе частот шириной 1 Гц.

    Суммарные продукты нелинейности 2-го порядка с частотой F = f_x + f_y образуются в результате взаимодействия спектральных составляющих группового сигнала с частотами f_x и (F - f_x ), где f₁f_xf₂ ; f₁(F - f_x ) f_2.

Общая мощность суммарных продуктов нелинейности 2-го порядка с частотой определяется числом составляющих группового сигнала с частотами f_x и f_у для которых выполняется условие f_x=F – f_у. площадью взаимно пересекающихся областей функций Р(f) и Р(F – f), где Р(f) – мощность составляющей группового сигнала с частотой f (рис. 3.17).

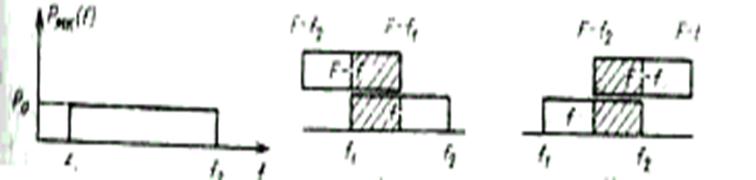
Рис. 3.16. Распределениемощ-Рис. 3.17. Взаимное расположение спектров

ности многоканального сигна-                f и  (F – f)

ла Рмк при работе системы

предыскажения

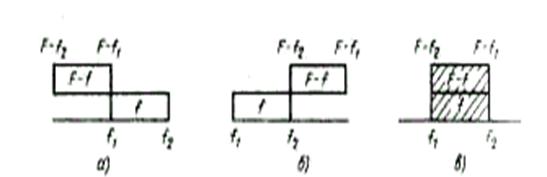
Рис. 3.18. Взаимное расположение спектров f и  (F – f)