Помехи в линейных трактах и каналах многоканальных систем передачи с ЧРК, страница 8

    На рис. 3.18, а и б показано взаимное расположение спектров f и (F – f) при F =2f₁ и F =2f₂  соответственно. Общая мощность суммарных продуктов нелинейности 2-го порядка на частоте F при этом равна нулю. При взаимном расположении рассматриваемых спектров, показанном на рис. 3.18, в, мощность

суммарных продуктов нелинейности 2-го порядка максимальна, а F = f₁ + f₂ .Таким образом, при изменении частоты F от 2 f₁, до (f₁ + f₂ )мощность рассматриваемых продуктов нелинейности линейно возрастает, а при изменении F от (f₁ + f₂ )до 2 f₂  линейно уменьшается (рис. 3.19), т. е. суммарные продукты нелинейности занимают полосу частот от 2 f₁    до 2 f_2.

    Численно значение суммарных продуктов нелинейности 2-го порядка на частоте F определяется с учетом (б) в (3.43) интегралом свертки

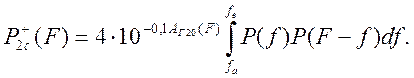                                           (3.47)

С увеличением частотыf_x частота f_у=F – f_х уменьшается, в результате чего их сумма F остается неизменной. Такие изменения взаимодействующих частот могут продолжаться до тех пор, пока они не станут равными. При дальнейшем увеличении f_х и уменьшении f_у взаимодействующие частоты, заменив друг друга, вновь создают уже учтенные ранее комбинации.

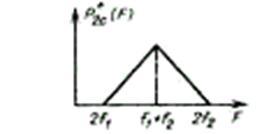
Рис. 3.19. Частотная зависимость мощности суммарных продуктов нелинейности 2-го порядка

                 

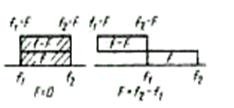
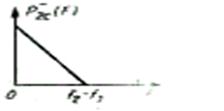
Рис. 3.20 Пределъно возможные         Рис. 3.21. Частотная

расположения спектров f и (F – f)        зависимость мощности  разнос-

                                                                 тных продуктов нелиней-

                                                                 ности 2-го порядка

Поэтому максимальное значение частоты f_х определяется из равенства f_х= f_у= F/2.

    Из рис. 3.17 следует, что в полосе частот от 2 f₁, до (f₁ + f₂ ) минимальное значение ,а в полосе частот от (f₁ + f₂ )до 2 f₂ .Таким образом, в (3.47) пределы интегрирования

                                                      (3.48)

    Разностные продукты нелинейности с частотой F = f_x - f_y образуются в результате взаимодействия спектральных составляющих группового сигнала с частотами f_x и ( f_х-F ). Общая мощность этих продуктов пропорциональна площади взаимно пересекающихся областей функций Р(f)и Р(f- F ). Для положительных значений F на рис. 3.20 показаны два предельно возможных взаимных положения спектров  fи  (f- F). Из этого рисунка следует, что разностные продукты нелинейности занимают полосу частот от F =0 до F= f₂ - f₁ , а мощность этих продуктов максимальна при F =0  и линейно уменьшается до нуля при F= f₂ - f₁ (рис. 3.21).

    Численное значение величины определяется также интегралом сверки

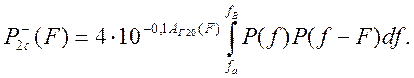                                    (3.49)

Пределы интегрирования легко определяются из рис. 3.20:

                                                                                  (3.50)

    После вычисления интегралов (3.47) и (3.49), используя соотношение (3.46), можно найти суммарную мощность продуктов нелинейности 2-го порядка на частоте F:

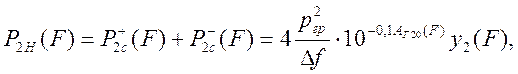                                       (3.51) 

где у₂(F)- функция спектрального распределения мощности продуктов нелинейности 2-го порядка, определяющая долю общей мощности этих продуктов, попадающую в узкую полосу частот со средней частотой F. Значения функции у₂(F) зависят от относительной ширины линейного спектра СП .По-

скольку нелинейные помехи в каналах системы создают только те продукты нелинейности, частоты которых совпадают с ее линейным спектром, практический интерес представляют частоты F пределах от  f₁ до f₂ .При, т. е. в диапазоне частот возникают только разностные продукты нелинейности 2-го порядка.

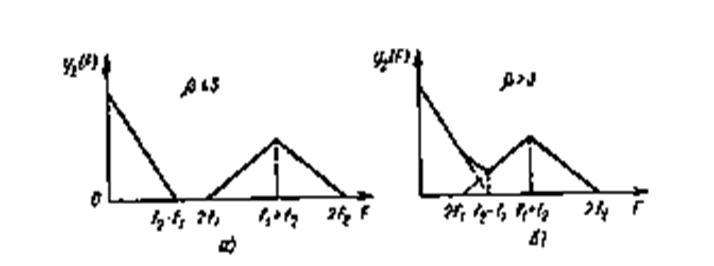
Рис. 3.22. Зависимость функции спектрального распределения мощ-

ности продуктов нелинейности 2-го порядка от частоты при относи-

тельной ширине линейного спектра (а) и (б)

Для этого случая

y₂(F)=1-F/ƒ                                                (3.52)

           В диапазоне частот 2ƒ₁Fƒ₂  создаются только суммарные продукты и                                                                                                             

                                                               y₂(F)=0,5(F-2ƒ₁)/ƒ

                                                                                                                             (3.53)

График функции у₂(F) для рассматриваемого случая приведен на рис. 3.22, а. При > 3 в диапазоне частот (ƒ_2- ƒ₁)F2ƒ₁  возникают как суммарные, так и разностные продукты нелинейности  у₂(F) и представляет собой сумму выражений (3.52) и (3.53) (рис. 3.22, 6).

Для практических расчетов удобно ввести безразмерную нормированную частоту

                        (F- ƒ₁ )/( ƒ_2- ƒ₁)                                                (3.54)

которая изменяется в пределах 0 1 при изменении  F от ƒ₁, до ƒ_2.Значение нормированной функции спектрального распределения мощности нелинейных помех 2-го порядка

                       ₂()=  при  0;

                                                                                                              (3.55)

                        у₂()=0,5 при  1

При   функция у₂() определяется суммой этих выражений. Заметим, что при  2 функция ₂()=0 , а при >>2  ₂()=1-/2. На рис. 3.23 приведено семейство характeристик ₂(), рассчитанных по формулам (3.55). Среди продуктов нелинейности 3- го порядка, как уже указывалось, наибольшее значение имеют продукты с частотами F= ƒ_x ƒ_y  ƒ_z .Распределения по спектру продуктов нелинейности с частотами (ƒ_x + ƒ_y   - ƒ_z )( ƒ_x + ƒ_y  + ƒ_z), (ƒ_x - ƒ_y   - ƒ_z) отличаются друг от друга и должны рассматриваться отдельно.

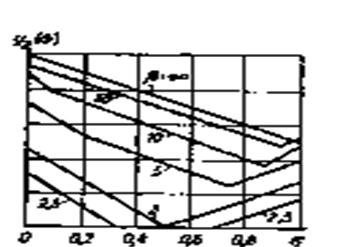
Рис. 3.23. Зависимость функции спектралъного распределения мощности продуктов нелинейности 2-го порядка от нормированной частоты  и относительной ширины линейного спектра.