Рассматривая любую автоматическую телефонную сеть необходимо обратить внимание на то, что максимальное количество соединений, которые можно одновременно установить в сети, существенно меньше общего числа абонентов. При этом, однако, абоненты не испытывают затруднений при пользовании телефонной связью. Объяснение заключается в том, что абонентские линии даже в дневные часы, когда совершается наибольшее количество вызовов, используются в среднем не более чем на 20% (то есть в течение 80% времени по ним не ведутся разговоры). Пропускная способность коммутационных полей, производительность управляющих устройств, количество приемников набора номера и других узлов АТС, а также число соединительных линий на сети рассчитываются таким образом, чтобы, с одной стороны, обеспечить высокое качество обслуживания абонентов, а, с другой стороны, не допустить непроизводительного использования оборудования. Поскольку вызовы поступают от абонентов в случайные моменты времени, а продолжительность разговора также является случайной величиной, возможно возникновение ситуации, в которой для обслуживания очередного поступившего вызова не найдется свободных линий или комплектов на АТС. В этом случае абоненту придется либо повторить вызов, либо дождаться освобождения занятых устройств. Частота возникновения отказов в обслуживании из-за занятости линий или комплектов и время ожидания абонентом их освобождения являются в данном случае показателями качества обслуживания. Пользование связью должно быть удобным для абонентов, поэтому необходимо, чтобы необходимость повторения вызовов по вине телефонной сети возникала нечасто, а ожидание установления соединения было небольшим. Для расчета количества оборудования АТС и числа межстанционных соединительных линий применяют специальные методы, созданные на основе математической теории – теории телетрафика.
Теория телетрафика оперирует не с самими телефонными станциями и сетями, а с их абстрактным представлением – математическими моделями систем распределения информации. Для того, чтобы правильно выбрать метод расчета, необходимо определить математическую модель, которая наилучшим образом соответствует рассматриваемому оборудованию. Математическая модель включает в себя три составляющие:
- входящий поток вызовов,
- дисциплину обслуживания,
- схему системы распределения информации.
Рассмотрим отдельно каждую из составляющих.
Потоком вызовов называется последовательность вызовов, поступающих в некоторые моменты времени. Как следует из определения, поток вызовов можно задать, указав моменты поступления вызовов, или интервалы времени между вызовами. Однако это возможно лишь в том случае, когда моменты поступления вызовов заранее известны. Если же поток вызовов имеет случайный характер, что чаще всего бывает в действительности, то его обычно характеризуют величиной интенсивности. Интенсивность потока вызовов m равна среднему числу вызовов, поступающих в единицу времени.
Вторым важным параметром, характеризующим процесс обслуживания вызовов, является длительность занятия обслуживающего устройства. Обслуживающими устройствами могут быть линии связи, соединительные пути в коммутационных полях АТС, станционные комплекты и другие элементы телефонных сетей. Длительности занятия узлов АТС и линий связи складываются из времени разговора между абонентами и времени, которое тратит абонент и станционное оборудование на установление соединения и разъединение. Величина длительности занятия так же как и моменты поступления вызовов чаще всего носит случайный характер. Поэтому в расчетах используется ее среднее значение t. Постоянная (одинаковая для всех вызовов) длительность занятия характерна для обслуживания вызовов управляющими устройствами АТС, которые совершают все действия по установлению соединений за одно и то же время, независимо от поведения абонентов. Поскольку при проектировании АТС методы расчета систем с постоянной длительностью обслуживания почти не используются, ниже будут рассматриваться только модели со случайной длительностью.
Интенсивность потока вызовов и средняя длительность занятия являются исходными данными для расчета количества устройств и линий связи. Основным способом получения этих данных являются измерения на действующих телефонных сетях. Удобнее измерять не интенсивность потока вызовов и среднюю длительность занятия в отдельности, а один общий параметр - величину телефонной нагрузки.
Телефонная нагрузка Y – это сумма длительностей занятия обслуживающих устройств. Если в течение периода времени измерения T поступило C вызовов, причем длительность занятия при обслуживании i-го вызова (i = 1, 2, … , C) равнялась ti, то телефонная нагрузка Y в этот период составит:
|
|
Если известна средняя длительность занятия ![]() , то нагрузку можно определить как
произведение средней длительности занятия на число поступивших вызовов:
, то нагрузку можно определить как
произведение средней длительности занятия на число поступивших вызовов:
|
|
Телефонная нагрузка, поскольку она представляет собой сумму длительностей занятия, измеряется в часо-занятиях. Ее можно измерить в течение одного или двух часов, в течение суток или месяца. По этой причине, оперируя величиной нагрузки, следует всегда иметь в виду период времени, в течение которого она измерялась. Так, например, одно устройство способно обслужить нагрузку не более 1 часо-занятия в течение одного часа.
Для того, чтобы величину нагрузки было удобнее сопоставлять с числом обслуживающих устройств, введено понятие интенсивности нагрузки. Интенсивность нагрузки - это нагрузка за единицу времени. Введена специальная единица измерения интенсивности нагрузки - Эрланг (Эрл), равная 1 часо-занятию за 1 час. Если известна интенсивность потока вызовов mи средняя длительность занятия t, то интенсивность поступающей нагрузки составит:
|
|
.
Таким образом, интенсивность телефонной нагрузки включает в себя две основные, характеристики поток вызовов.
Интенсивность телефонной нагрузки зависит от категории абонентов и, как правило, изменяется в широких пределах по часам суток, дням недели и сезонам года. Максимальные значения интенсивности нагрузки наблюдаются обычно по будням: наибольшее число вызовов от служебных телефонных аппаратов поступает в утренние или дневные часы, а от квартирных - в вечернее время. Сезонные колебания величины нагрузки на сети телефонной связи железнодорожного транспорта связаны, в частности, с увеличением пассажиропотока в летние месяцы. На рис. 9.1 представлен пример распределения телефонной нагрузки в течение одних суток. Нагрузка, создаваемая одной и той же группой абонентов в разные дни, может быть распределена неодинаково, но закономерности возрастания и убывания ее интенсивности в определенные часы обычно сохраняются.
Качество обслуживания абонентов в любое время суток не должно опускаться ниже допустимого предела; поэтому число обслуживающих устройств рассчитывается на основе наибольших значений интенсивности нагрузки. Час, в течение которого телефонная нагрузка максимальна, называется часом наибольшей нагрузки (ЧНН). Заметим, что понятия нагрузки в ЧНН и интенсивности нагрузки в ЧНН совпадают, так как речь идет о величине нагрузки за единицу времени – 1 час.
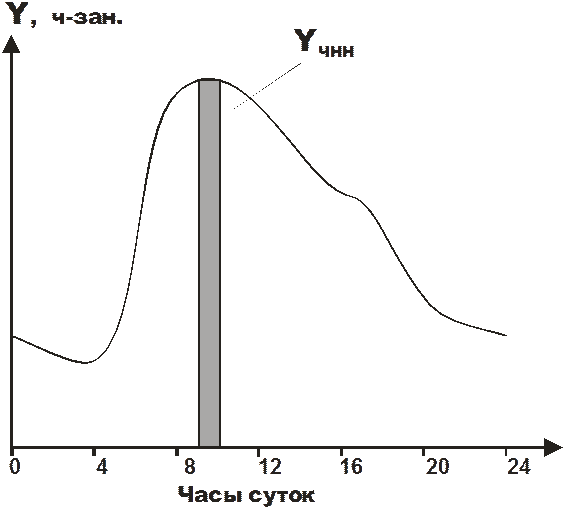
Рис.9.1 Пример распределения нагрузки по часам суток
В примере, представленном на рис. 9.1, ЧНН расположен между 9 и 10 часами утра. Отношение нагрузки в ЧНН - YЧНН - к значению нагрузки YС, поступающей от той же группы абонентов в течение суток, называется коэффициентом концентрации нагрузки:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.