ПРОИЗВОДСТВА И ЕГО РЕАЛИЗАЦИЯ НА ЭВМ.
Приведенные ниже алгоритмы расчета позволяют реализовать на ЭВМ методику математического моделирования, основные принципы которой описаны в Главе 2.
3.1. Блок переработки природного газа.
3.1.1. Риформинг метана.
В аппарат первичного риформинга входит два материальных потока: пар и природный газ (см. рис. 8). Расход и состав образующейся газовой смеси определяется покомпонентным сложением с учетом формулы (2.29). Температура на выходе – регулируемый параметр, поэтому ее значение задается до начала расчета.
Из [74] известно, что в первичном риформинге протекают две независимые равновесные реакции (2.13) и (2.14). Они описываются системой из двух уравнений типа (2.27), которая решается итерационным методом [19]. Пусть a – количество СН4, прореагировавшего по реакции (2.13), b – количество СО прореагировавшего по реакции (2.14) (в нм3/ч). Для первого шага итерации были заданы некоторые начальные значения a и b. Тогда, считая, что реакции (2.15) протекают до конца, операциями покомпонентного сложения и вычитания рассчитали состав равновесной газовой смеси. Затем, вычислив константы равновесия реакций (Кр1 и Кр2) при температуре Тр (формулы (7,8) Приложения III), записали систему уравнений в следующем виде (с учетом формул (2.28-2.29):
![]()
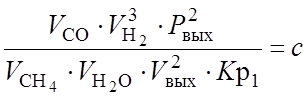 (3.1)
(3.1)
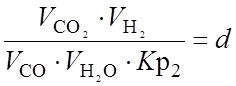 (3.2)
(3.2)
где Vi – объемы компонентов в равновесной газовой смеси, нм3; Vвых – общий объем равновесной газовой смеси, нм3.
Таким образом, a и b есть решения системы уравнений (3.2-3.3), если c = 1и d = 1. В противном случае необходимо задать новые значения a = a + Da и b = b + Db. Алгоритм моделирования представлен на рис. 15.
Здесь и далее на блок-схемах приняты следующие обозначения:
- прямоугольник – входные и выходные данные или рассчитываемые параметры;
- штриховой прямоугольник – принимаемые значения для итерационных вычислений;
- ромб – условие;
- двойная стрелка - выполнение математических операций в соответствии с формулами, отмеченными над стрелкой;
- простая стрелка – передача начальных или расчетных данных.
На схемах обозначена передача наиболее существенных (с точки зрения логики и последовательности расчета) данных, т.к. обозначение передачи всех данных слишком загромождает схемы.
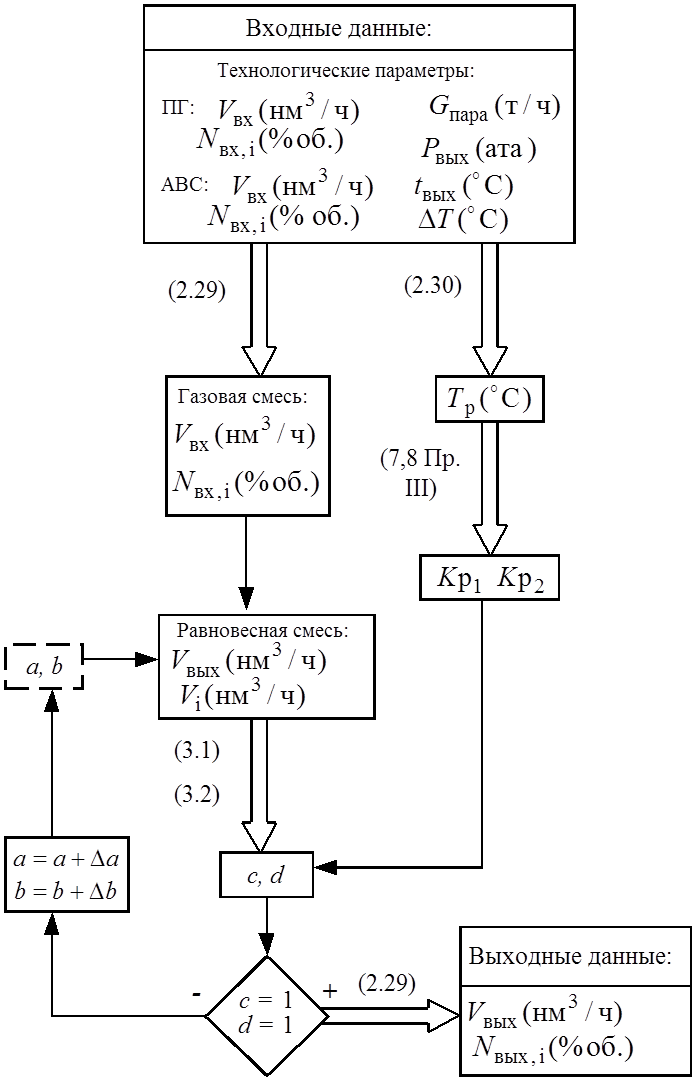
Рис. 15. Блок-схема моделирования стадии первичного риформинга.
В аппарат вторичного риформинга подаются паро-газовая смесь (ПГС) из первичного риформинга и паро-воздушная смесь (ПВС). В I зоне (над катализатором) происходит полное сгорание кислорода с водородом по реакции (2.16).
Расход и состав газовой смеси до и после 1-й зоны определялся покомпонентным сложением и вычитанием согласно стехиометрии реакции (2.16). Во 2-й зоне на катализаторе протекают реакции (2.13,2.14), описываемые системой уравнений (3.1,3.2). Так как реактор адиабатический, то температура на выходе до расчета неизвестна, поэтому необходимо добавить уравнение теплового баланса (2.63), записанное в виде:
Q1 + Q2 + Q3 + Q4 - (Q5 + Q6 +Q7) = f (3.3)
Тепловые эффекты реакций (2.13,2.14) известны [74]. При определении энтальпий газовых смесей по формуле (2.9) использовали зависимости H = f(t), полученные для каждого компонента по уравнению (2.2).
Пусть e – температура на выходе из реактора, °С. На первом шаге итерации были заданы некоторые значения a,b,e. Таким образом, для стадии вторичного риформинга a,b,e есть решения системы уравнений (3.1-3.3), если c = 1, d = 1 и f = 0. В противном случае необходимо задать новые значения a = a + Da, b = b + Db и e = e + De. Алгоритм моделирования представлен на рис. 16.
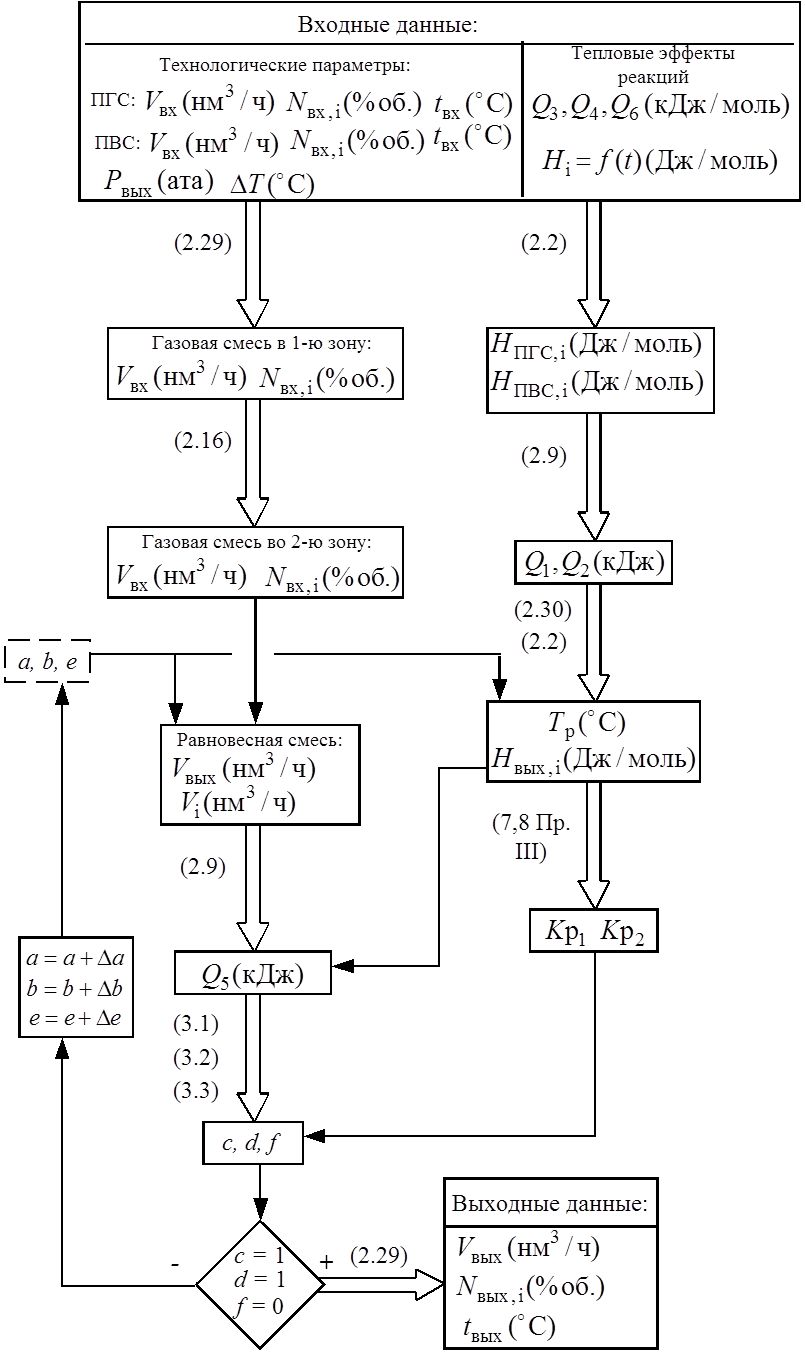
Рис. 16. Блок-схема моделирования стадии вторичного риформинга.
3.1.2. Конверсия СО и очистка газа.
Конверсию СО по реакции (2.14) проводят в 2 стадии, отличающиеся температурой процесса [81]. На обеих стадиях применяют адиабатические реакторы [74]. Поэтому для определения состава и температуры газа на выходе необходимо решить систему из двух уравнений. Одно из них - уравнение (3.2), второе – уравнение теплового баланса:
Q1 + Q2 - (Q3 + Q4) = f (3.4)
Итерационные вычисления организованы аналогично стадиям первичного и вторичного риформингов.
Алгоритм моделирования одинаков для каждой стадии конверсии СО и приведен на рис. 17.
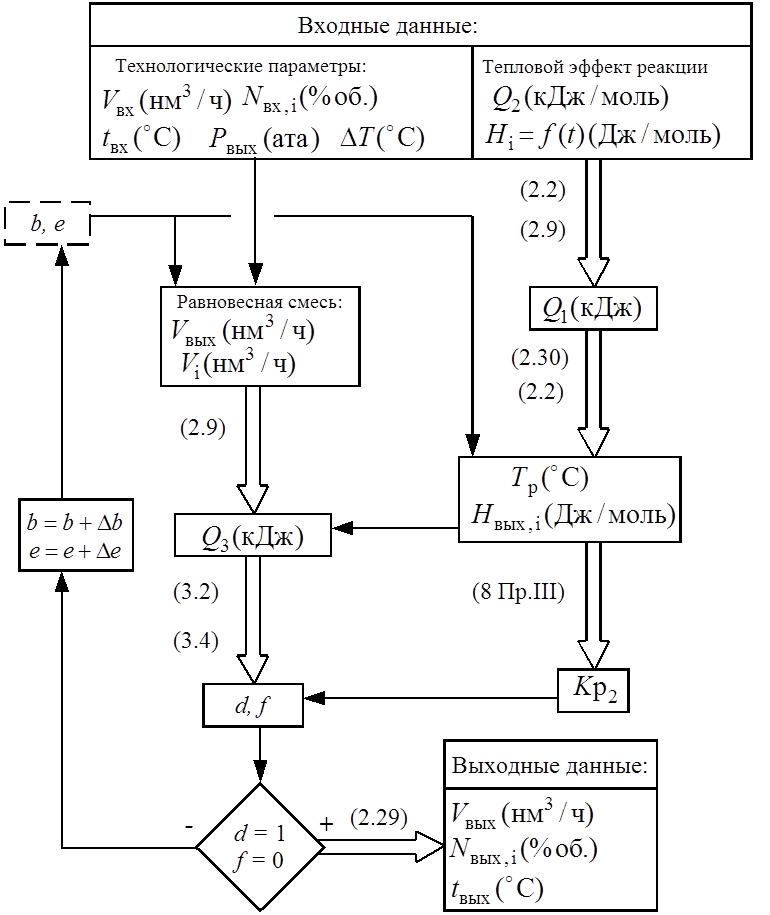
Рис. 17. Блок-схема моделирования стадии конверсии СО.
За равновесную температуру абсорбции приняли температуру глубокорегенерированного раствора МЭА, подаваемого на верх абсорбера. Равновесное давление СО2 над раствором определяем по практическим данным [74]. Реакции (2.19,2.20) протекают до конца, поэтому состав газа после метанирования рассчитывали покомпонентным сложением и вычитанием согласно стехиометрии реакций.
Алгоритм моделирования представлен на рис. 18.
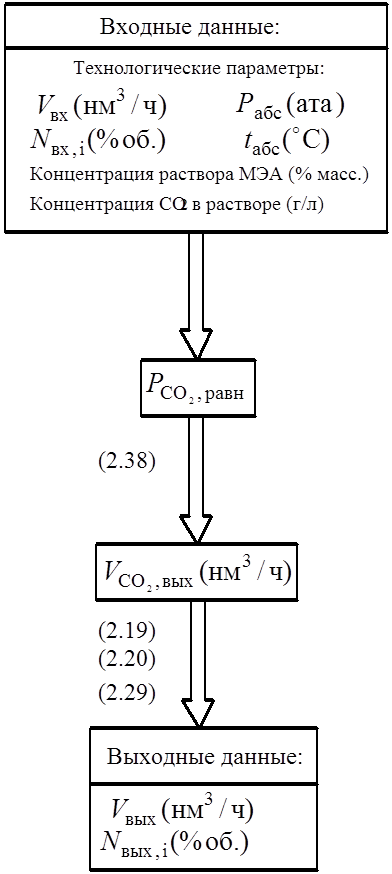
Рис. 18. Блок-схема моделирования стадии очистки.
3.2. Блок выработки пара высокого давления.
3.2.1. Котел-утилизатор.
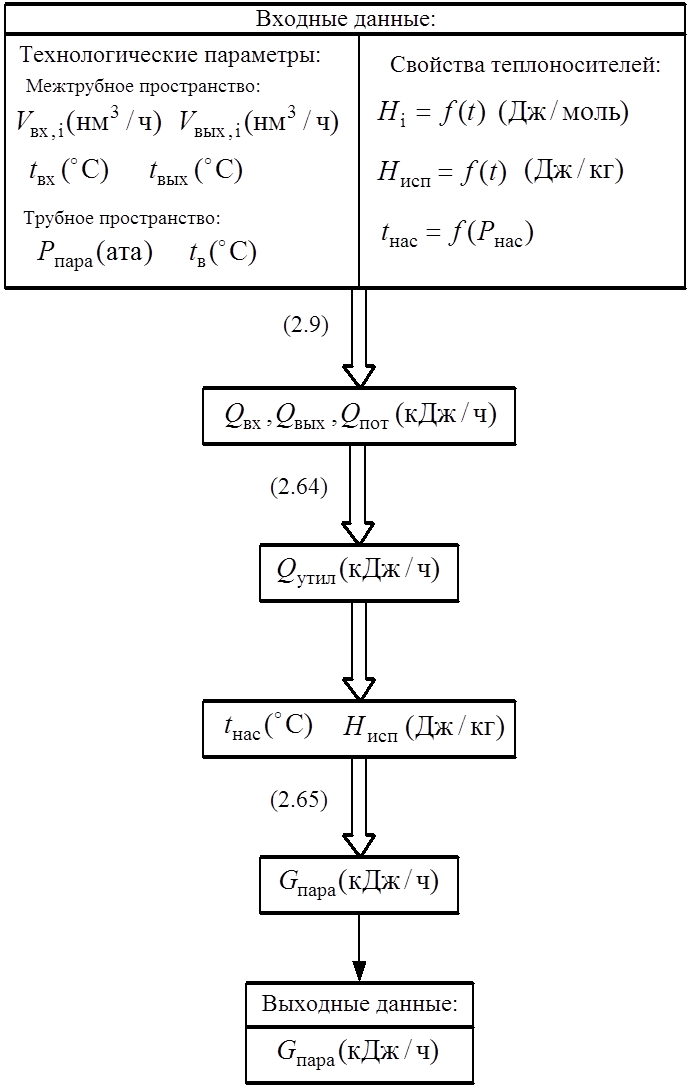
Рис. 19. Блок-схема моделирования котла-утилизатора.
3.2.2. Вспомогательный котел.
Количество пара, вырабатываемого во вспомогательном котле, определяли из баланса выработки и потребления пара высокого давления. Из теплового баланса котла рассчитывали необходимый расход природного газа. Для этого уравнение (2.66) записали в виде:
Q1 + Q2 + Q3 - (Q4 + Q5 + Q6) = f (3.5)
Расчет по уравнению (3.5) вели методом итераций. Пусть е – расход природного газа во вспомкотел. Далее исходя из стехиометрии реакций (2.26) и принятого значения коэффициента избытка воздуха рассчитывали материальный баланс процесса горения: количество воздуха, необходимое для горения, и количество и состав дымовых газов. Затем определяли величины, входящие в уравнение (3.5) и проверяли сходимость теплового баланса. Если f = 0 с заданной точностью, то е есть решение уравнения (3.5). Алгоритм расчета показан на рис. 20.
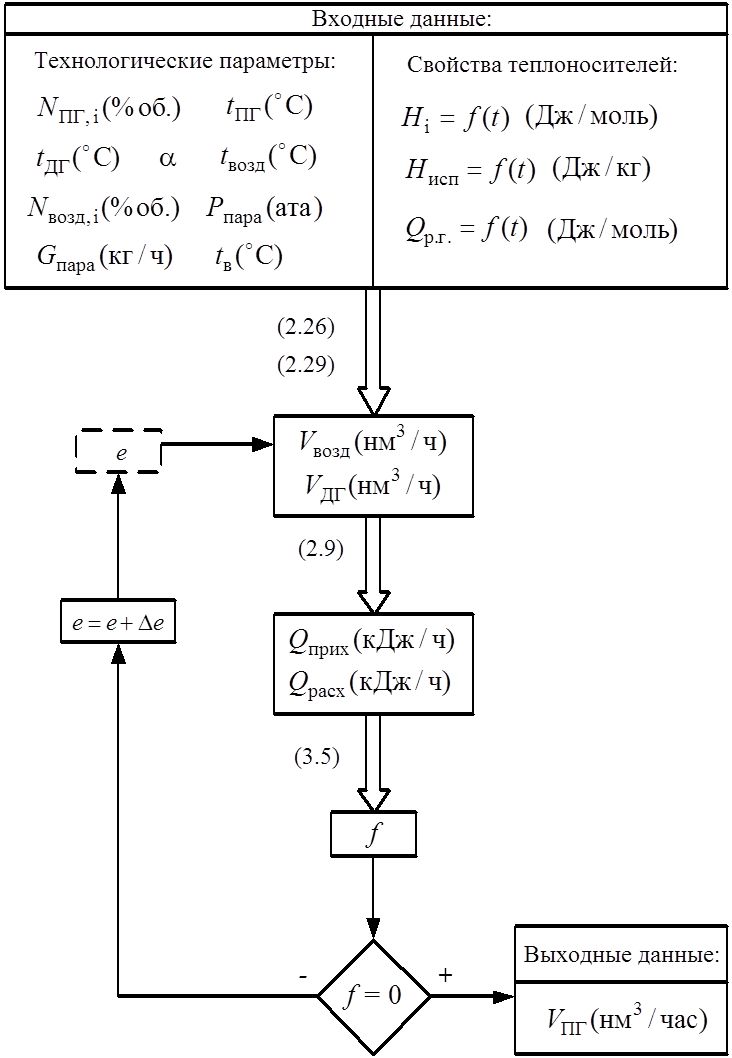
Рис. 20. Блок-схема моделирования вспомогательного котла.
3.3. Блок синтеза аммиака.
В соответствии с рекомендациями из [66,74] мы предположили, что после стадии очистки в газовой смеси присутствуют только H2, N2, CH4, Ar, т.к. концентрации СО, СО2 и Н2О пренебрежимо малы.
Объем и состав потока 0 (см.
рис. 14) следуют из расчета стадии очистки. Состав потока 01 неизвестен,
поэтому приняли начальные значения расходов каждого из компонентов ![]() (i = 1,2..5) в нм3/ч. Состав потока 1
рассчитали покомпонентным сложением. Далее по уравнениям (15-18) Приложения III определили концентрацию аммиака в
газовой смеси после вторичной конденсации и, тем самым, потоки 2,3.
(i = 1,2..5) в нм3/ч. Состав потока 1
рассчитали покомпонентным сложением. Далее по уравнениям (15-18) Приложения III определили концентрацию аммиака в
газовой смеси после вторичной конденсации и, тем самым, потоки 2,3.
Пусть a – количество NН3, прореагировавшего по реакции (2.21). Для первого шага итерации задали некоторое значение a и вычислили константу равновесия Кр (уравнение (14) Приложения III) при температуре Тр (формула (2.30)), записали уравнение (2.27) в следующем виде (с учетом формул (2.28-2.29):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.