Основные понятия теории вероятностей (Краткие теоретические сведения и задания на контрольную работу № 1)

Контрольная работа №1.

Тема: Основные понятия теории вероятностей.

Краткие теоретические сведения.

События.

Под событием в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти.

Примеры: А – появление герба при бросании монеты; В – попадание в цель при выстреле; С – взрыв на подстанции силового трансформатора; D – решение на первом практическом занятии 5 задач.

События обозначаются латинскими буквами.

Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные.

Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.

Пример: успешная сдача экзамена, при выполнении условий экзаменатора.

Невозможным называется событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S.

Пример: вода в сосуде при температуре + 20^оС и нормальном атмосферном давлении не будет находиться в твердом состоянии; сдача экзамена невозможна, если не решена ни одна из контрольных работ.

Случайным называют событие, которое при осуществлении совокупности условий S может произойти, а может не произойти.

Пример: при бросании монеты, может выпасть герб, а может надпись; количество студентов, присутствующих на занятии.

Виды случайных событий.

События называются несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Пример: выстрел по мишени исключает появление события «промах»; брошена монета: появление герба, исключает появление надписи. События «появился герб и надпись» - несовместные.

События называются совместными, если они могут произойти одновременно.

Пример: при бросании игральной кости появление четного количества очков и число выпавших очков – 4.

Несколько событий образуют полную группу, если в результате испытания появится, хотя бы одно из них. Или, появление хотя бы одного из событий полной группы есть достоверное событие.

В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.

Пример: Купили два лотерейных билета. Обязательно произойдет одно и только одно из следующих событий: «выигрыш выпал на первый билет, и не выпал на второй», «выигрыш выпал на второй билет, не выпал на первый», «выигрыш выпал на оба билета», «выигрыш не выпал на оба билета». Эти события образуют полную группу попарно несовместных событий.

События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Пример: появление гербы и появление надписи при бросании монеты.

Действия над событиями.

Суммой двух событий А и В называется событие С, состоящее в выполнении события или А или события В, или обоих вместе.

Пример 1: событие А – попадание при первом выстреле, В – попадание при втором выстреле, С = А+В – событие, заключающееся в попадании вообще, или при первом выстреле, или при втором, или при обоих.

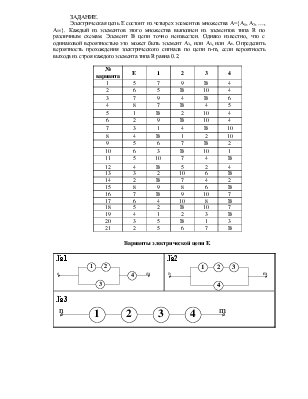
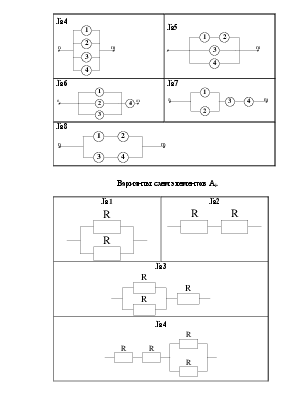
Пример 2: Опыт состоит в бросании игральной кости. Событие A_i (i = 1, 2, 3, 4, 5, 6) – выпадение i числа очков; событие А – выпадение четного числа очков, В – выпадение нечетного числа очков, С – выпадение числа очков, кратного трем, D – выпадение числа очков, больше трех. Выразите события А, В, С и D через A_i.

Решение: Событие А наступает тогда и только тогда, когда наступает А2, или А₄, или А₆. Это означает, что А = А₂ +А₄+А₆.

Рассуждая аналогично, имеем: В = А₁ + А₃ +А₅, С = А₃+А₆, D = А₄+А₅+А₆.

Произведение двух событий А и В называется событие С, состоящее в совместном выполнении и события А, и события В.

Пример: А₁, А₂, А₃ – события, заключающиеся в промахах в цель при трех