IX Спектральный метод анализа электрических цепей
9.1 Понятие о спектрах сигналов
Периодический сигнал
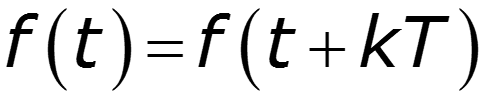
- период - любое целое число

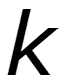
Простейший периодический сигнал
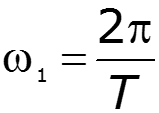
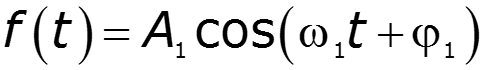
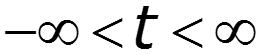
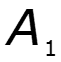
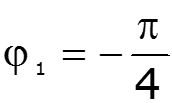
![]()
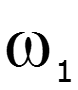
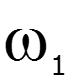
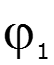
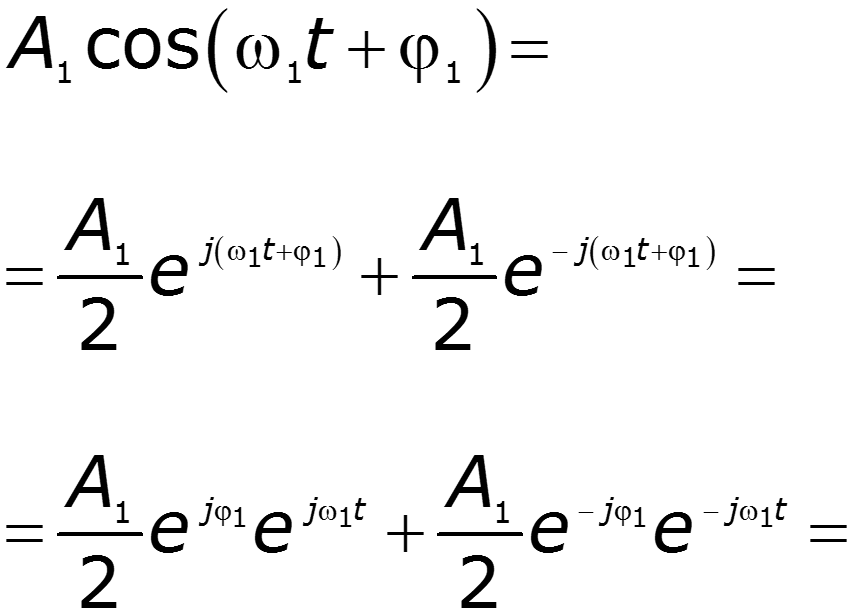
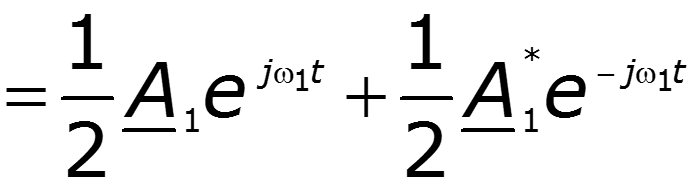
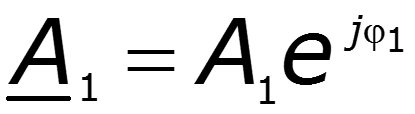
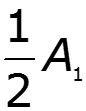
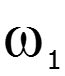
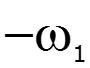
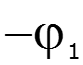
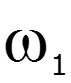
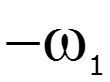
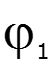
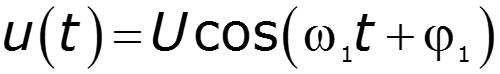
![]()
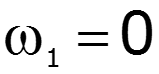
Если
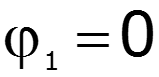
Тогда
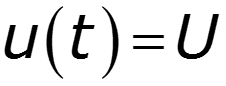
Постоянное напряжение
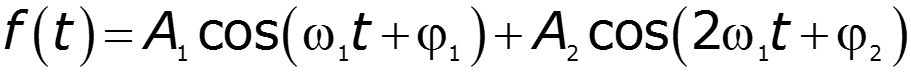
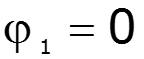
![]()
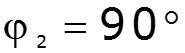
![]()
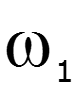
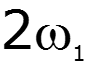
![]()
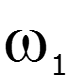
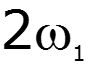
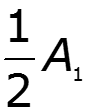
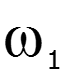
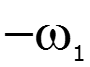
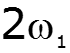
![]()
![]()
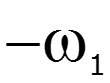
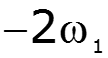
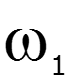
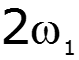
![]()
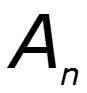
Совокупность амплитуд - спектр амплитуд Совокупность начальных фаз - спектр фаз
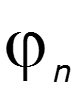
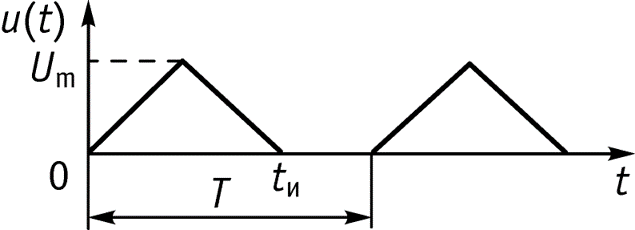
2. Спектральный метод анализа при непериодическом негармоническом воздействии входной сигнал представляется в виде интеграла Фурье
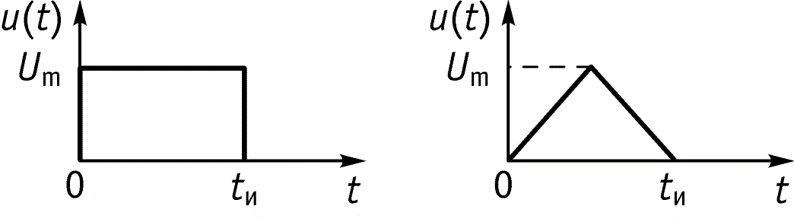
9.2 Спектры периодических сигналов
Периодические несинусоидальные ток и напряжения возникают в цепи при следующих режимах работы:
3. Источник постоянный или синусоидальный, один или несколько элементов цепи периодически изменяются во времени
![]()
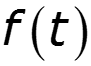
1. Тригонометрическая форма ряда Фурье
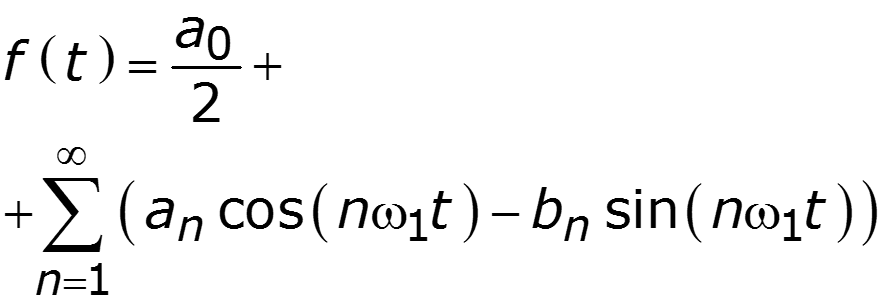
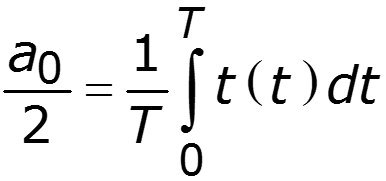
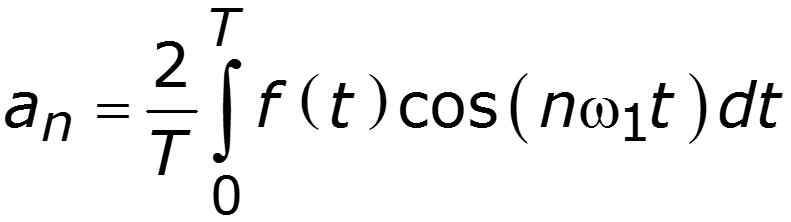
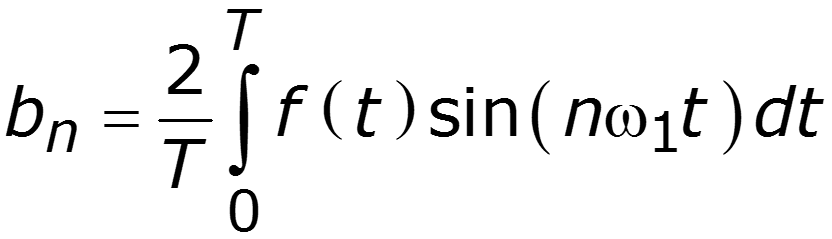
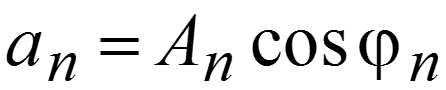
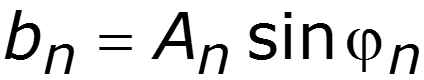
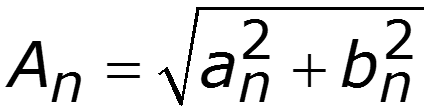
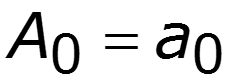
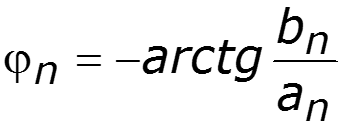
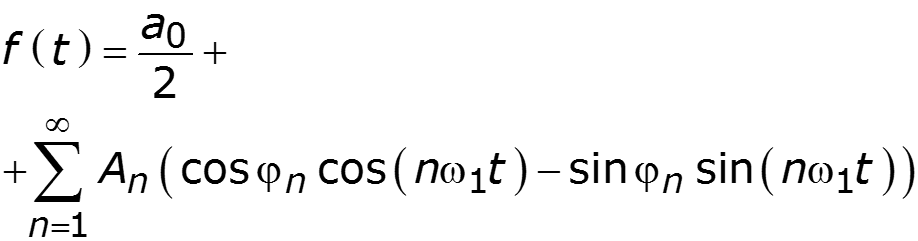
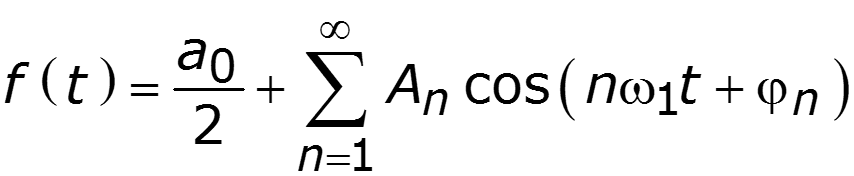
Спектр амплитуд
Спектр фаз
2. Комплексная форма ряда Фурье
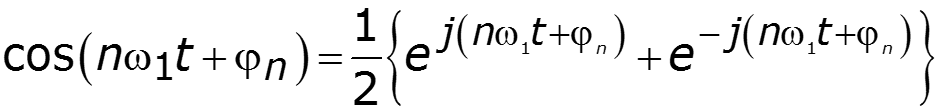
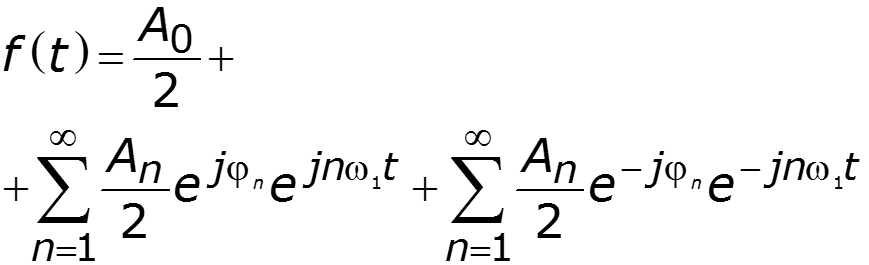
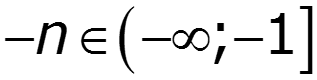
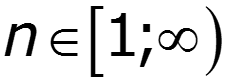
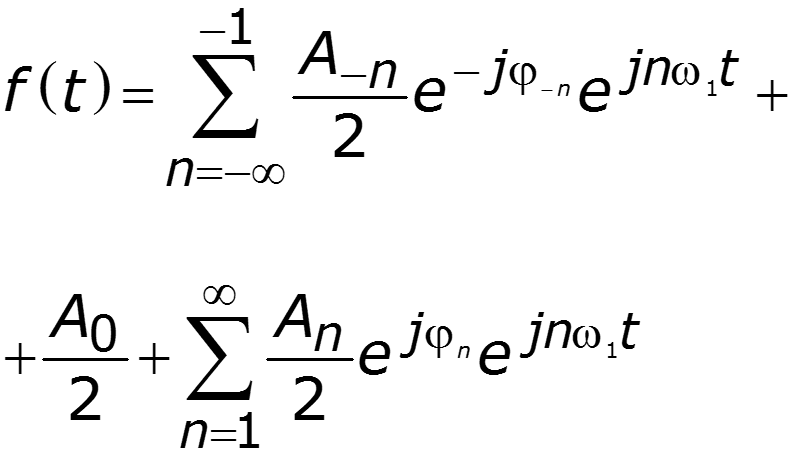
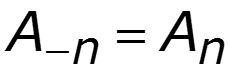
- четная функция
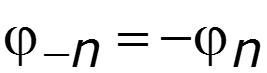
- нечетная функция
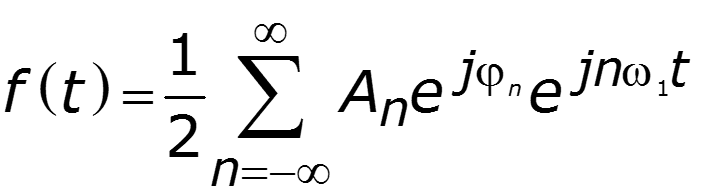
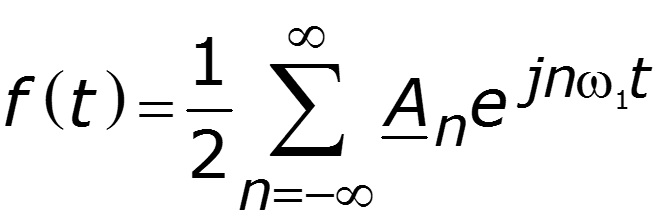
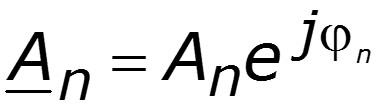
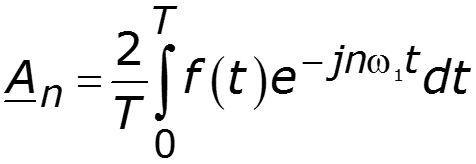
Спектр амплитуд
Спектр фаз
Вывод 1. Спектр периодического сигнала является дискретным или линейчатым 2. Расстояния между спектральными линиями - период сигнала
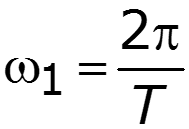

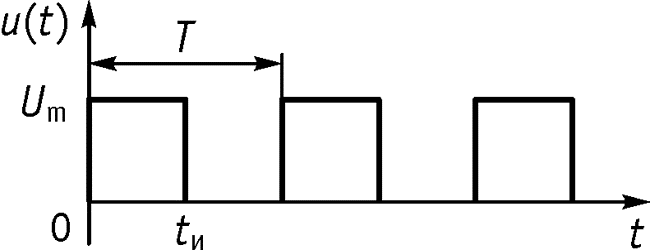
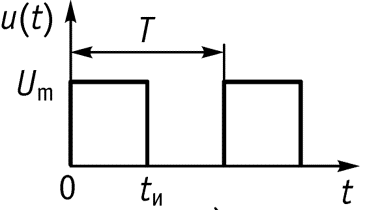
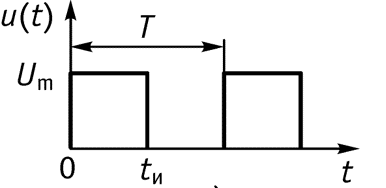
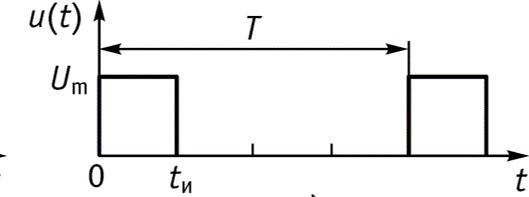
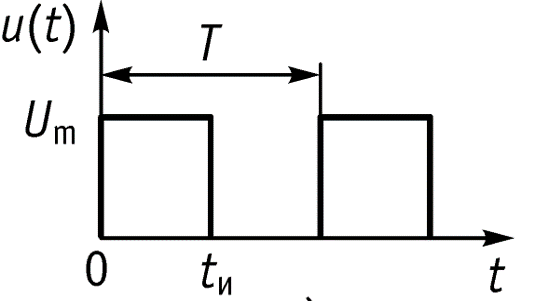
9.3 Спектр периодической последовательности прямоугольных импульсов
![]()
- длительность импульса
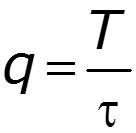
- амплитуда
![]()
- скважность
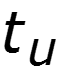
- длительность импульса
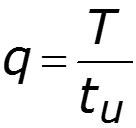
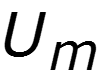
- амплитуда
- скважность
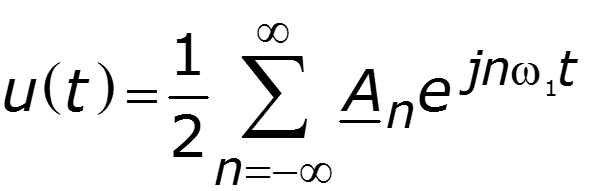
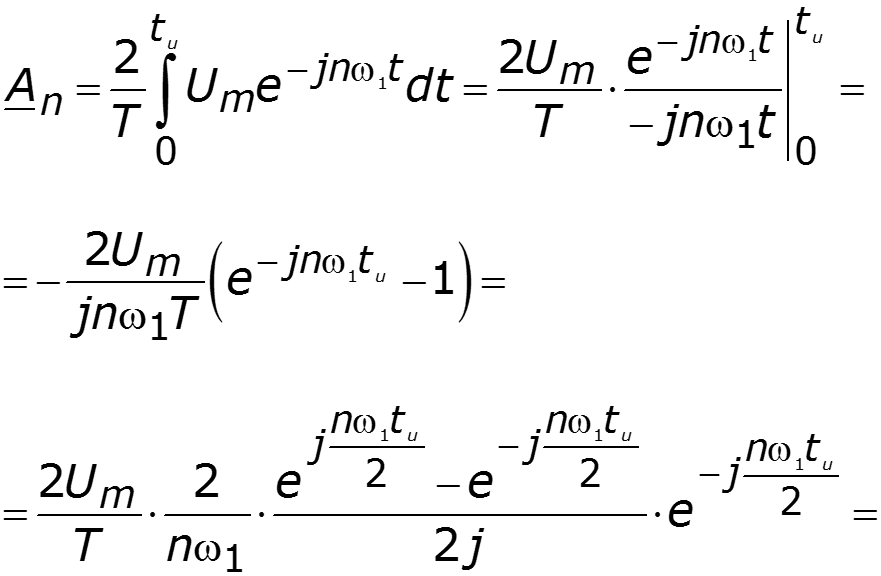
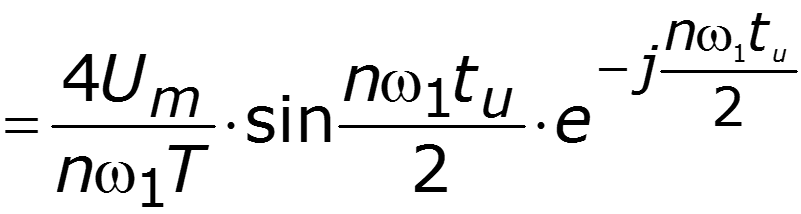
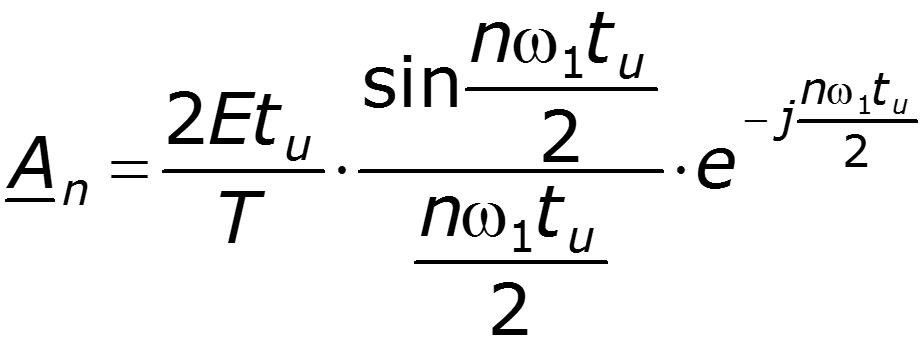
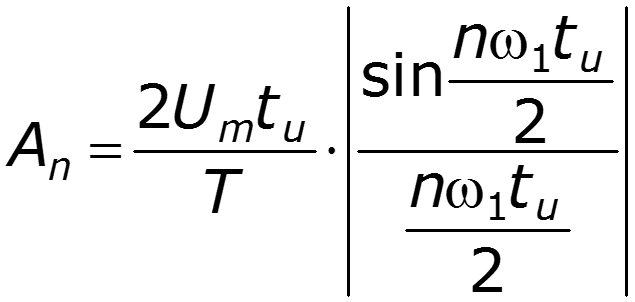
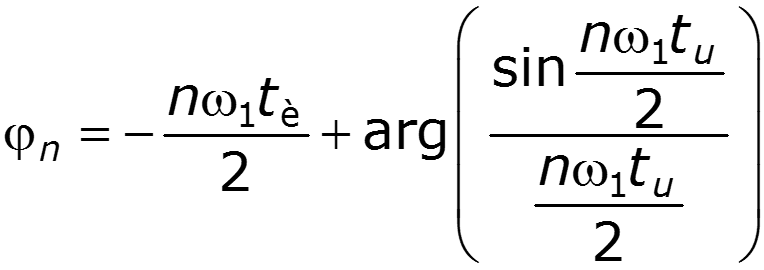
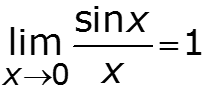
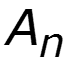
Нули
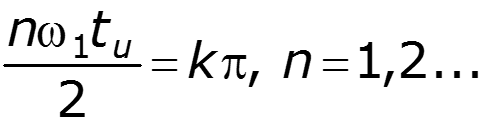
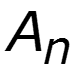
Частоты, на которых амплитуды равны нулю
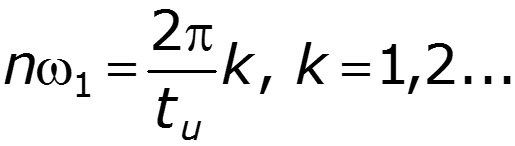
Номера гармоник, амплитуды которых равны нулю
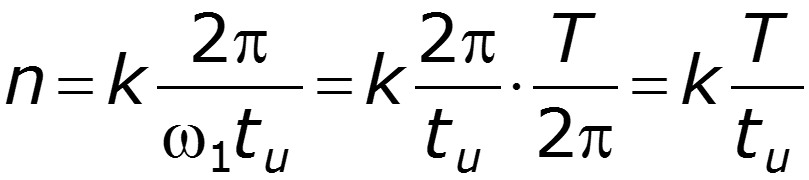
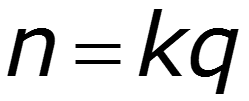
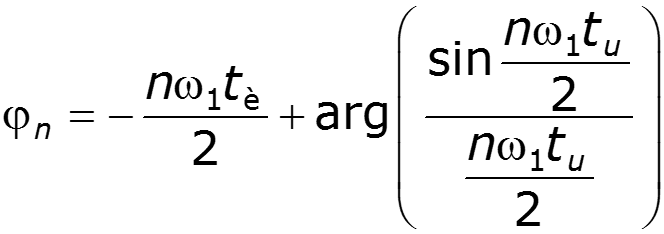
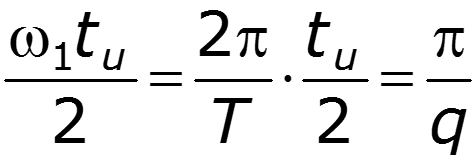
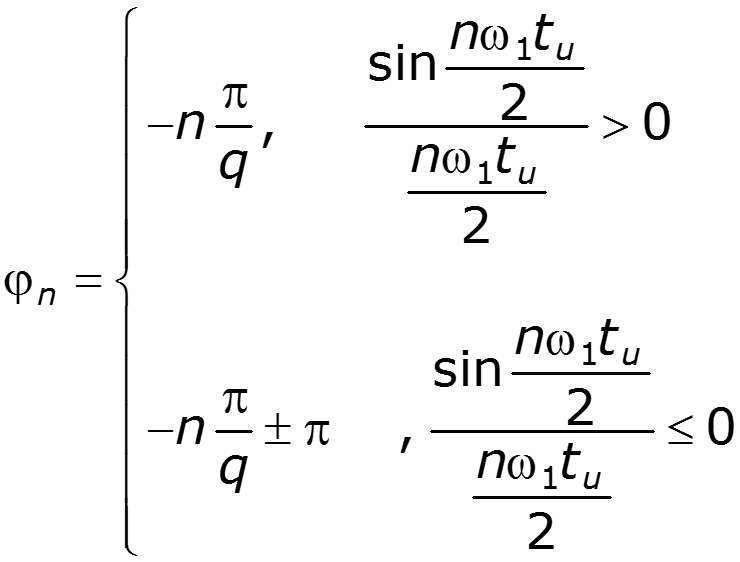
Построим амплитудный и фазовый спектры для различных значений скважности
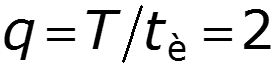
,
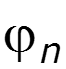
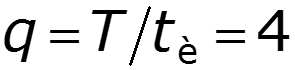
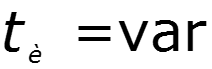

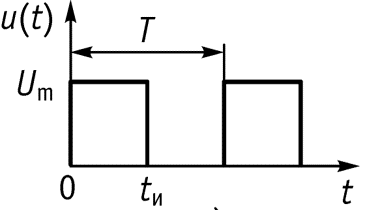
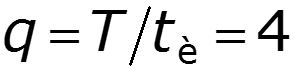
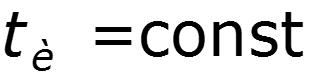
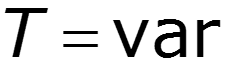
Выводы
1. Огибающая амплитудного спектра изменяется по закону функции 2. Огибающая имеет нули на частотах ( n = 1, 2, 3, …)
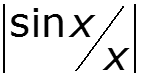
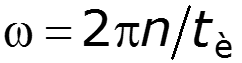
3. Спектр дискретный. Расстояние по частоте между гармоническими составляющими равно 4. Количество составляющих между нулями равно
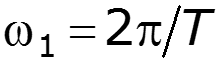
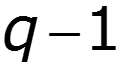
5. При и увеличении (уменьшении) расстояние между гармоническими составляющими остается постоянным, а расстояние между нулями огибающей уменьшается (увеличивается)
![]()

6. При и увеличении (уменьшении) периода T расстояние между нулями огибающей остается постоянным, а расстояние между составляющими уменьшается (увеличивается)
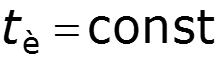
9.4 Анализ цепи при воздействии периодического несинусоидального сигнала
Порядок расчета
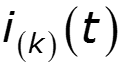
2. Рассчитать токи и напряжения в схеме при воздействии на нее каждой гармоники. Необходимо помнить:
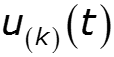
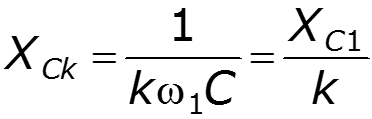
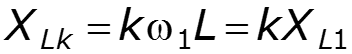
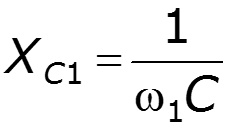
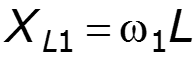
3. Пользуясь принципом наложения, определить токи и напряжения в цепи
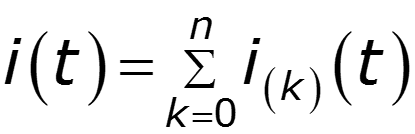
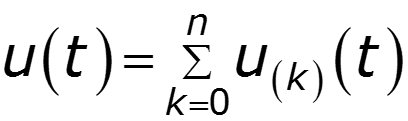
Действующие значения тока и напряжения
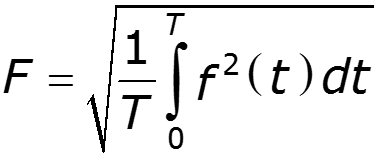
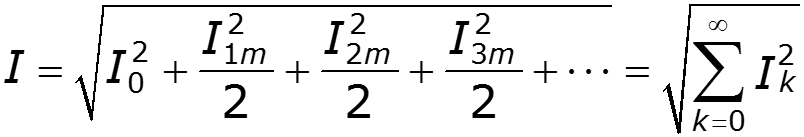
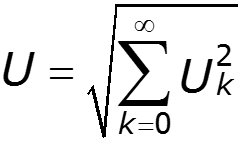
Действующее значение не зависит от начальных фаз отдельных гармоник
Средние по модулю значения тока и напряжения
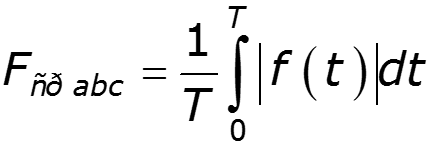
Зависит от амплитуд и начальных фаз гармоник
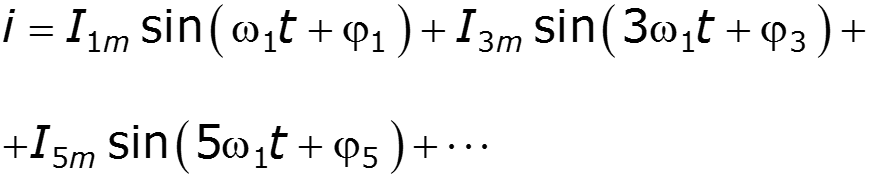
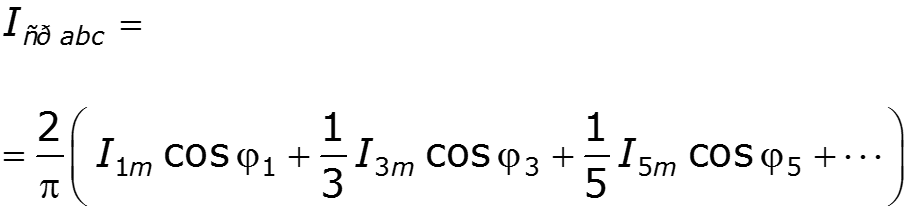
Активная, реактивная и полная мощности периодического негармонического сигнала
Активная мощность угол между током и напряжением k-ой гармоники
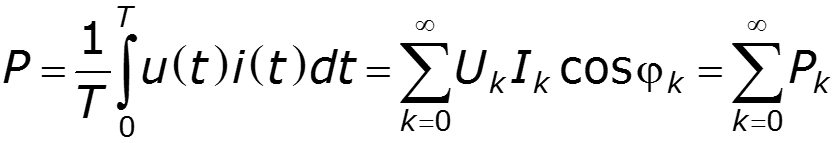
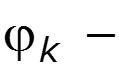
Реактивная мощность Полная мощность
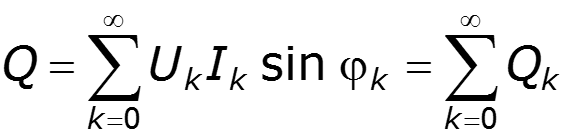
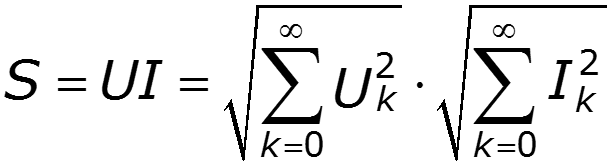
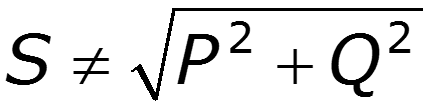
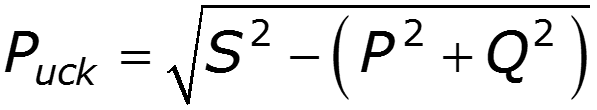
Коэффициенты, характеризующие периодический негармонический сигнал
1. Коэффициент мощности
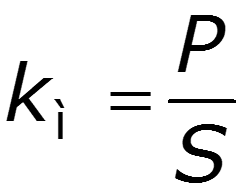
2. Коэффициент формы для гармонического колебания
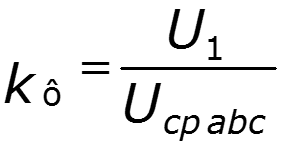
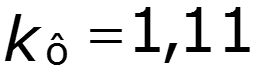
3. Коэффициент искажения для гармонического колебания
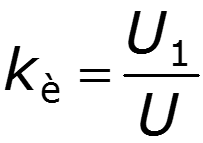
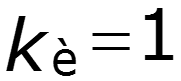
4. Коэффициент амплитуды для гармонического колебания
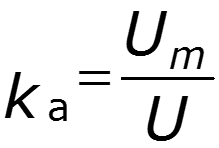
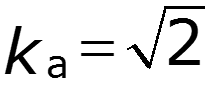
5. Коэффициент гармоник для гармонического колебания
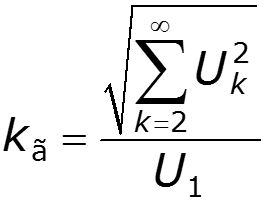
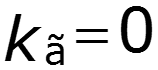
Пример
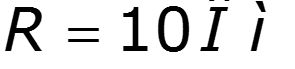
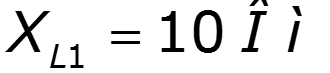
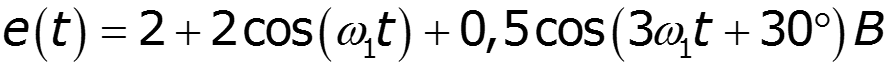
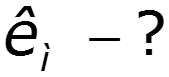
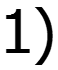
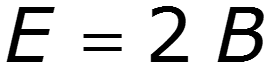
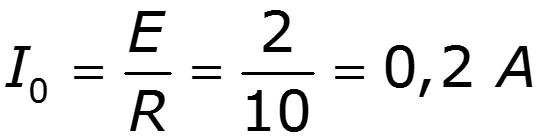
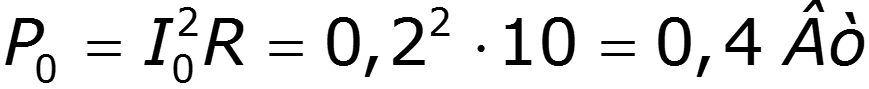
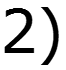
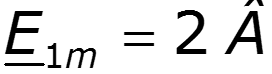
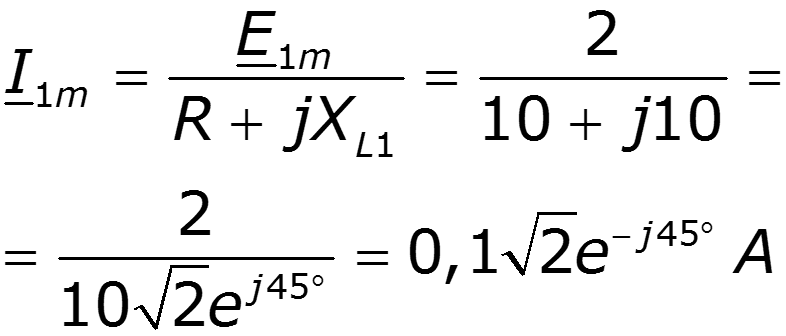
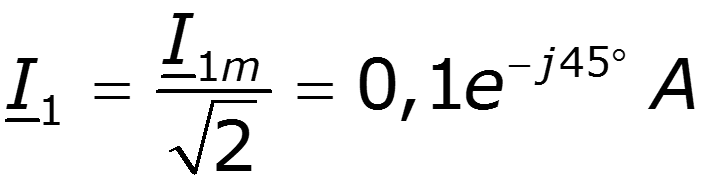
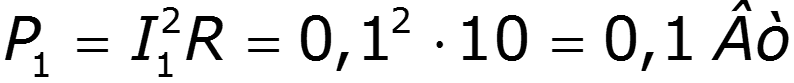
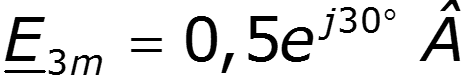
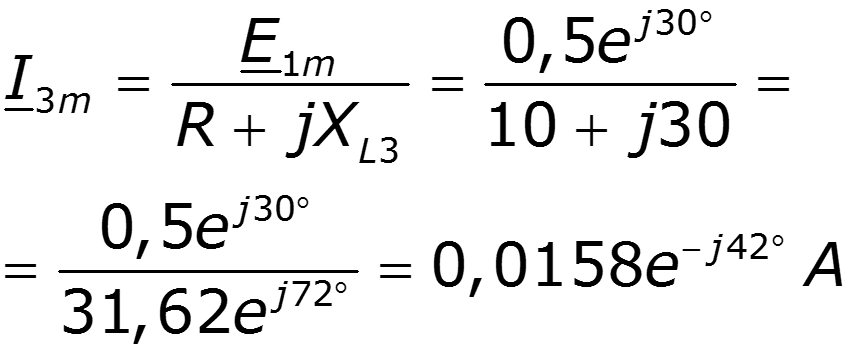
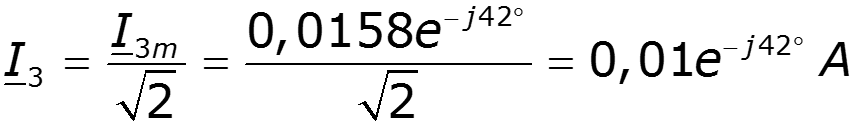
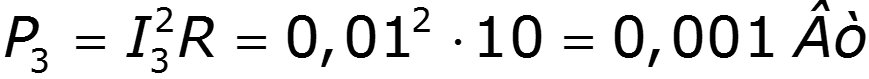
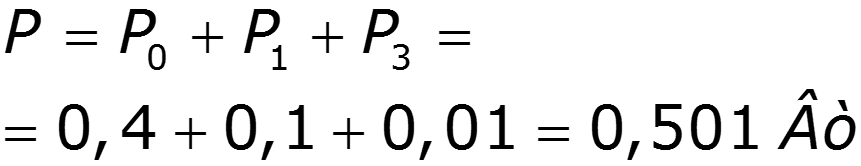
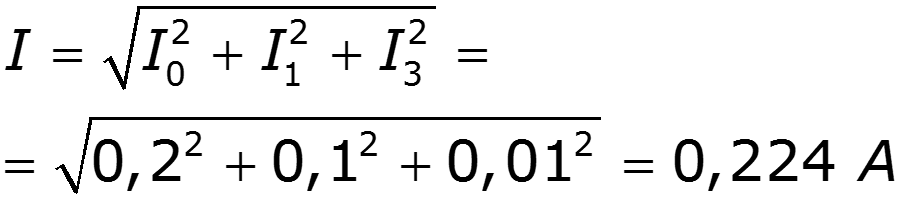
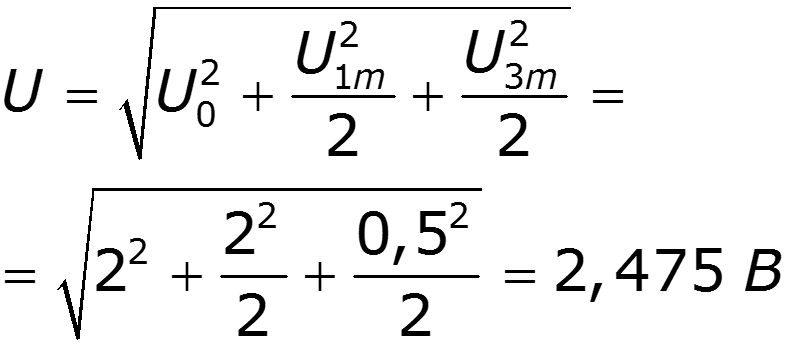
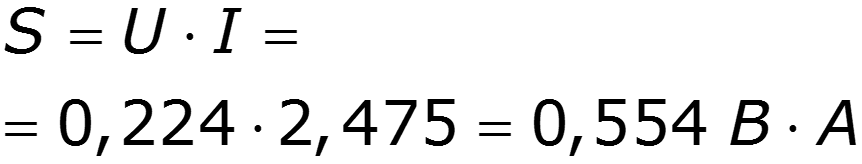
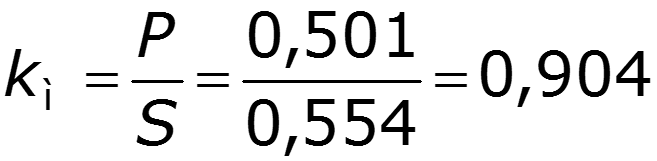
9.5 Спектры непериодических сигналов
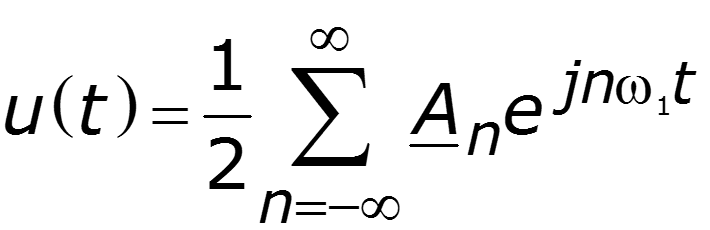
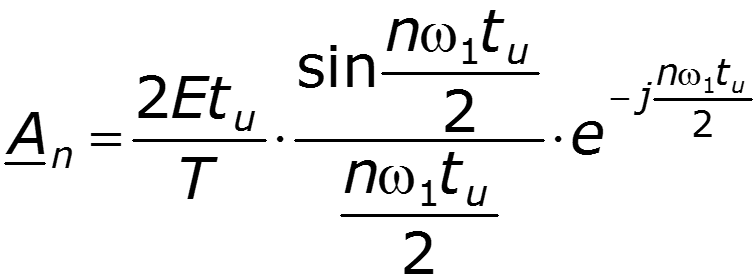
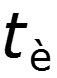
Если при постоянном увеличивать Т, то спектральные линии станут располагаться гуще, а их амплитуды уменьшатся
При и от периодической последовательности прямоугольных импульсов перейдем к одиночному импульсу Спектр одиночного импульса – сплошной, он содержит бесконечно большое число гармоник с бесконечно малыми амплитудами

![]()
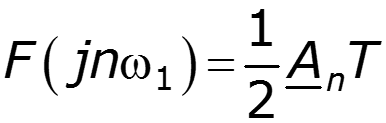
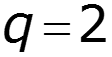
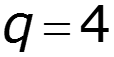
![]()
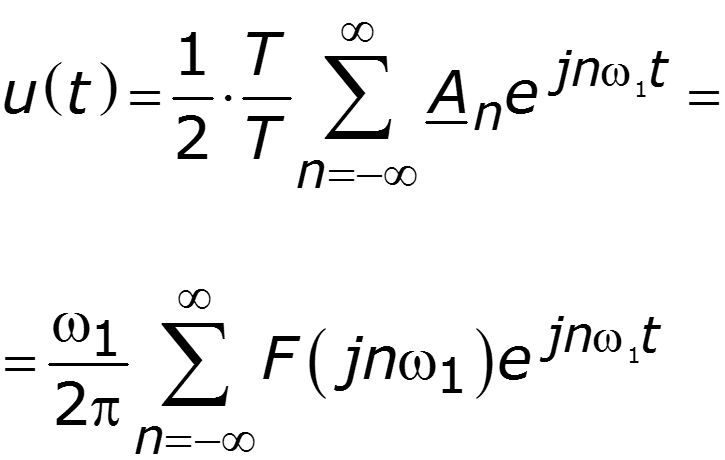
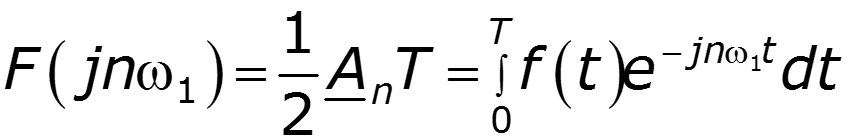
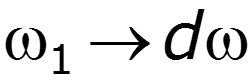

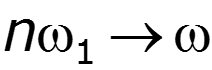
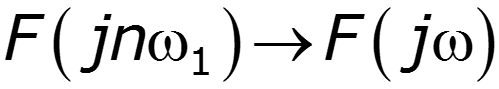
- спектральная плотность сигнала
Прямое преобразование Фурье
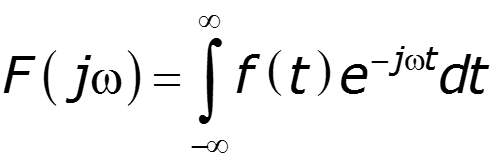
позволяет определить спектральную плотность сигнала
Обратное преобразование Фурье
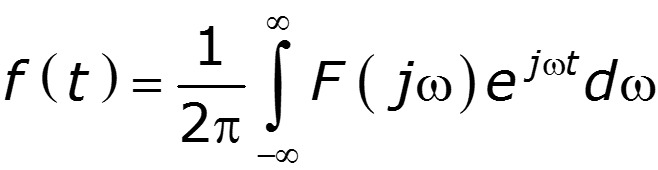
позволяет определить сигнал по его спектральной плотности
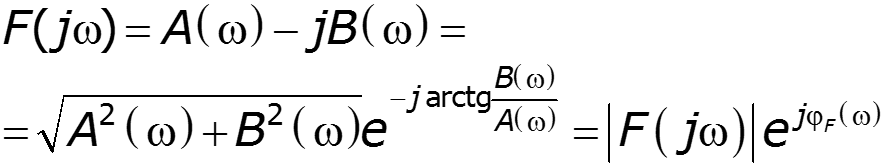
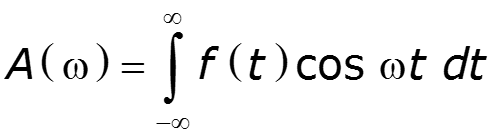
- вещественная часть спектра - мнимая часть спектра
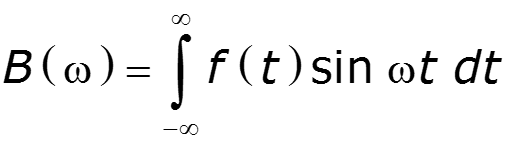
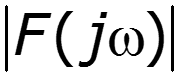
– спектральная плотность амплитуд (амплитудный спектр), функция четная – фазовый спектр, функция нечетная
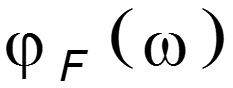
Физический смысл прямого преобразования Фурье
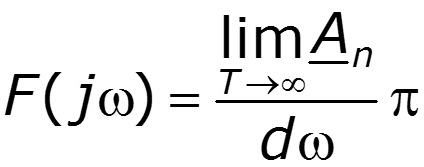
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.