7. Переходные процессы.
Классический метод анализа
7.1. Основные понятия
 |
Виды коммутации:
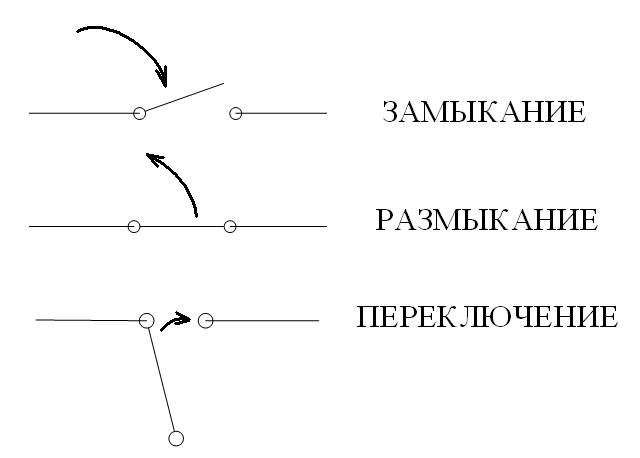
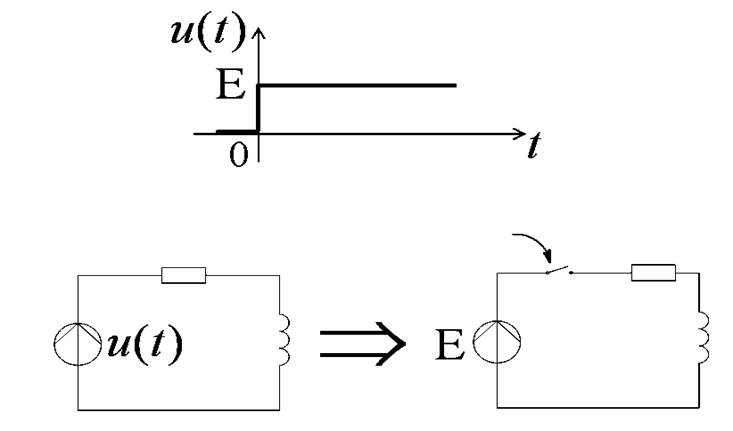
Условные обозначения:
t=0_ (т.е. t<0) – установившийся режим до коммутации
t=0 - момент коммутации
t=0+ - первый момент после коммутации
-
установившийся режим после коммутации
Коммутация в резистивной цепи
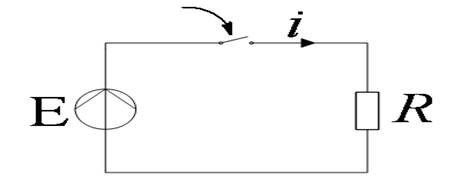
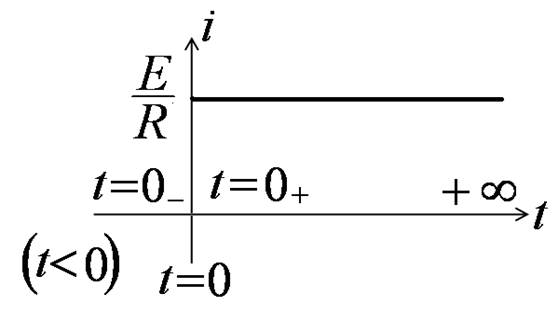
Коммутация в цепи с реактивным элементом
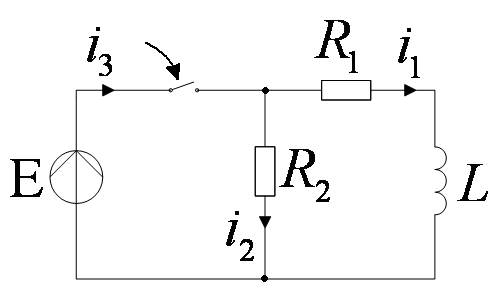
Найдём ток i1(t)
|
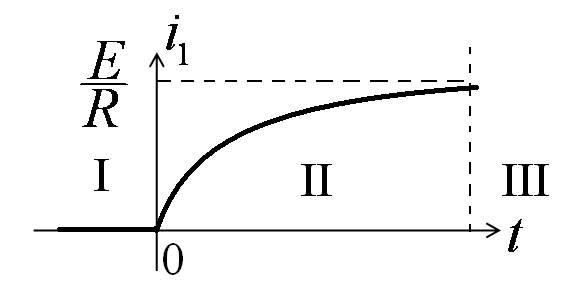
I.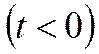
Установившийся
режим до коммутации.
II.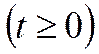
Переходный
процесс.
III.
Установившийся
режим после коммутации.
Вывод:
В первый момент после коммутации ток в индуктивности остаётся таким же, каким он был до коммутации, а затем плавно изменяется.
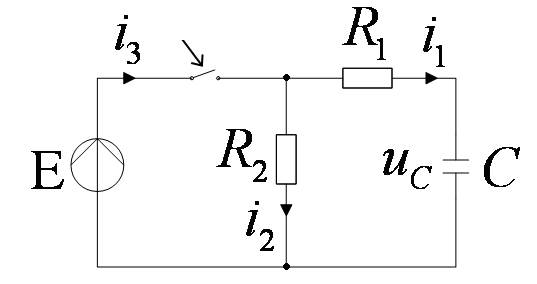
Найдём напряжение uc(t)
Напряжение на ёмкости uc в момент коммутации скачком измениться не может.
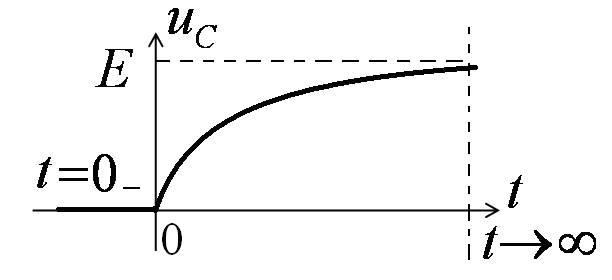
7.2. Законы коммутации.
 |
1-ый закон
Ток в индуктивности не может измениться скачком.
Пример:
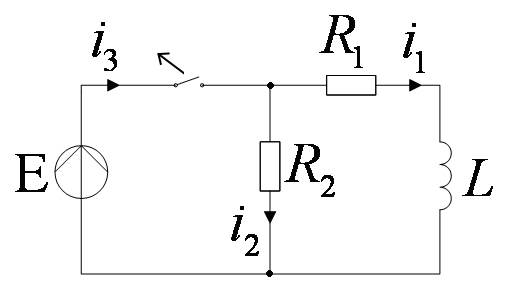
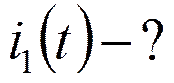
t<0:
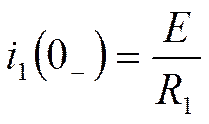
По 1-му закону коммутации
t=0+ :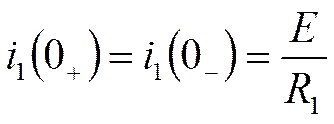 
t=¥: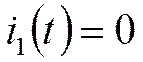 
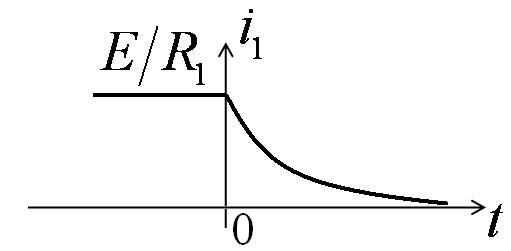
Так как в первый момент после коммутации ток в индуктивности не зависит от напряжения на ней, катушка индуктивности будет вести себя как идеальный источник тока.
:
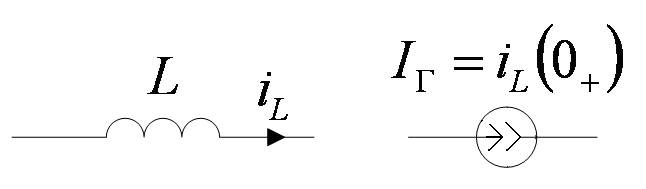
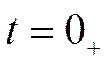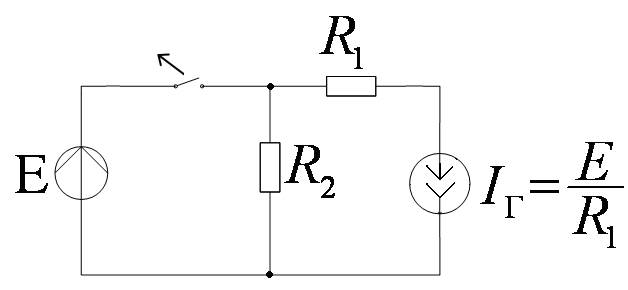
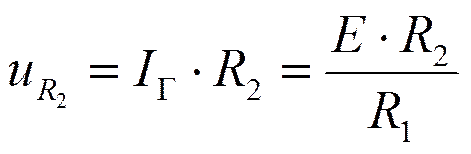
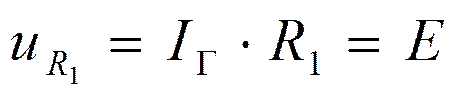
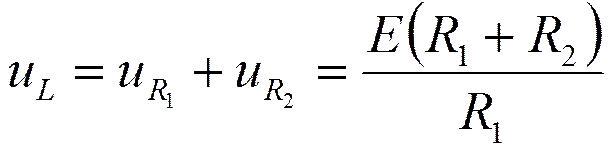
2-ой закон
Напряжение на ёмкости не может измениться скачком.
Пример:
: 
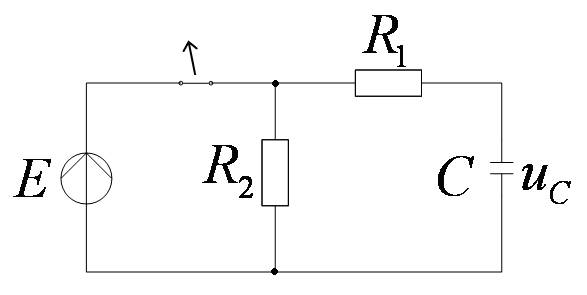
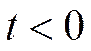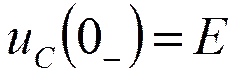
По 2-му закону коммутации
t=0+ :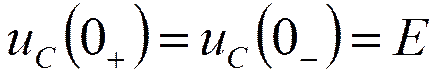 
: 
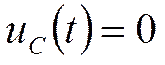
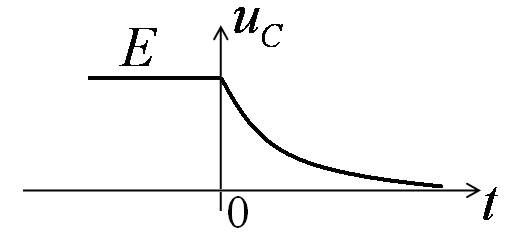
В первый момент после коммутации конденсатор ведёт себя как идеальный источник напряжения.
:
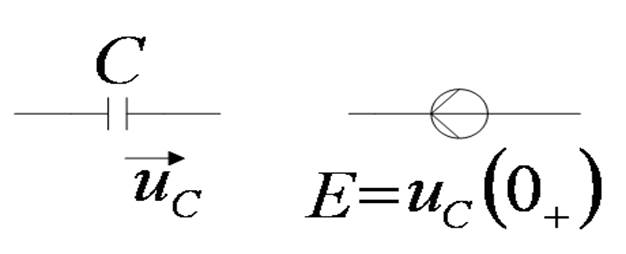
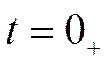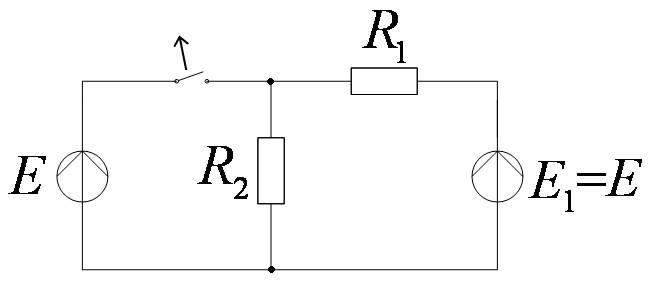
Начальные условия
Значения токов в индуктивностях iL(0+) и напряжений на ёмкостях uC(0+) называются начальными условиями (независимыми) – ННУ.
Нулевые ННУ и
ненулевые ННУ.
7.3. Переходные
процессы в цепях первого порядка.
Короткое замыкание цепи RL
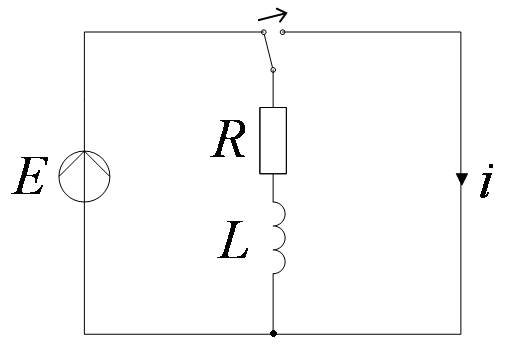
По 2-му закону Кирхгофа
: 
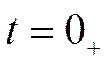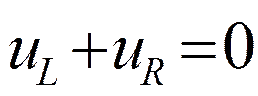или
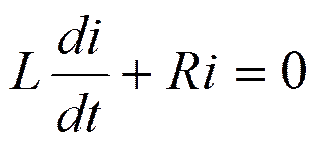
Дифференциальное уравнение – однородное
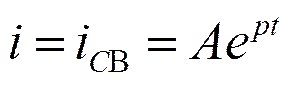, где
p – корень характеристического уравнения
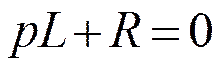
Он равен
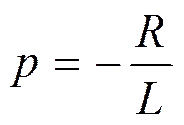
Свободная составляющая тока
-
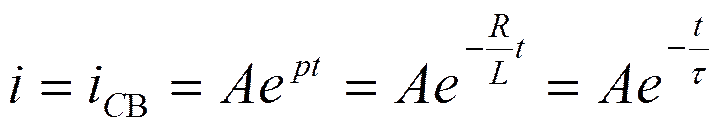
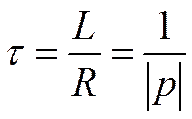постоянная времени (цепи или переходного процесса)
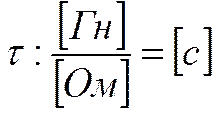
Постоянную А найдём из начальных условий:
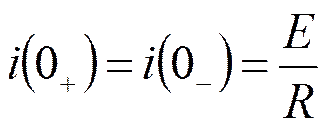
Тогда:
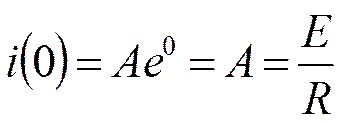
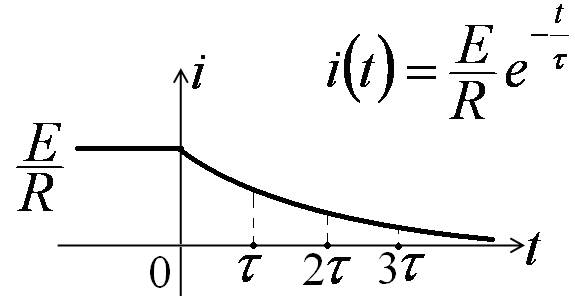
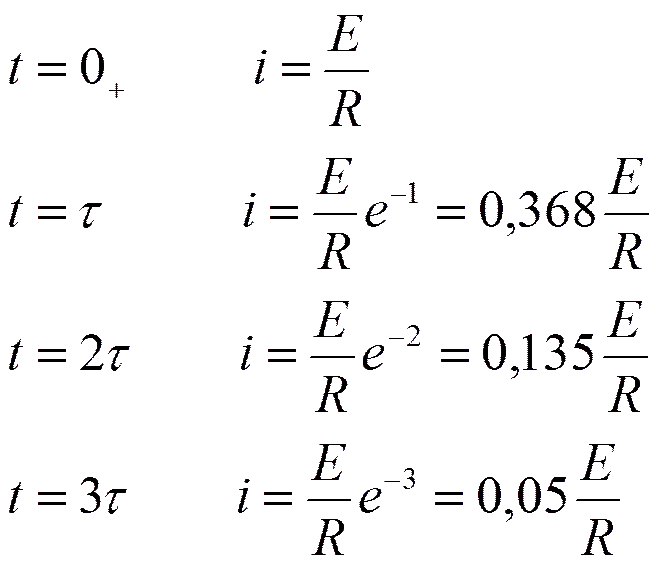
Принято считать, что
tпп = 3t.
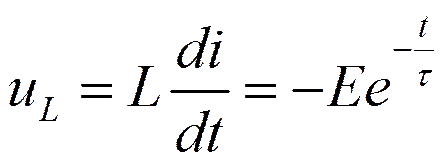
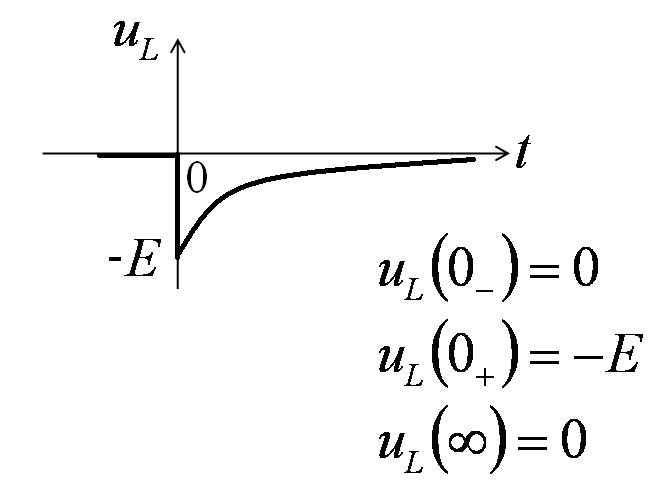
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
