XVIII Цепи с распределенными параметрами
18.1 Однородные линии
Электрическая цепь, у которой геометрические размеры соизмеримы с длинной волны ( ) и у которых индуктивность, емкость, сопротивление и проводимость распределены по длине, называется электрической цепью с распределенными параметрами.
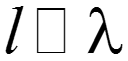
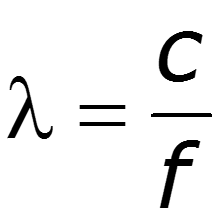
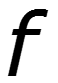
- частота сигнала

- скорость света
Если геометрические размеры электрической цепи намного меньше длины волны ( ), то такая электрическая цепь называется цепью с сосредоточенными параметрами. Условие – условие квазистационарности
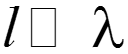
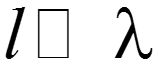
Если только один из размеров не удовлетворяет условию , то такая цепь называется длинной линией. Различают: однородные и неоднородные длинные линии.
![]()
Первичные параметры однородной длинной линии.
равны значениям соответствующих распределенных параметров, измеренных на отрезке линии единичной длины (1 км для линии проводной связи и 1 м для линии радиосвязи).
К первичным параметрам относятся:
–сопротивление R; –проводимость G; – индуктивность L; – емкость С.
Вторичные параметры длинной линии
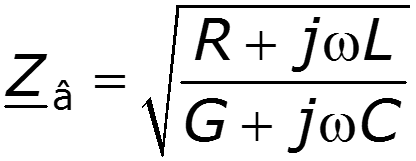
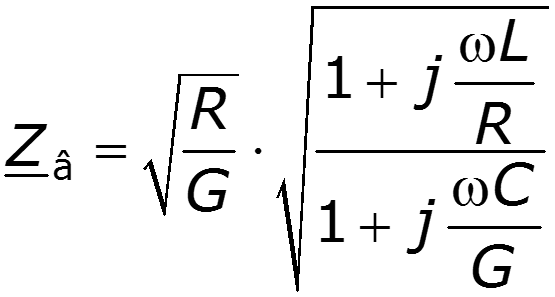
Для однородной линии, рассматриваемой между выходными и входными выводами как симметричный четырехполюсник, волновое сопротивление равно характеристическому сопротивлению .
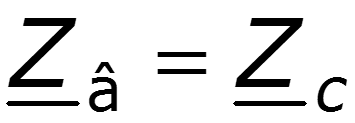
2. Коэффициент распространения
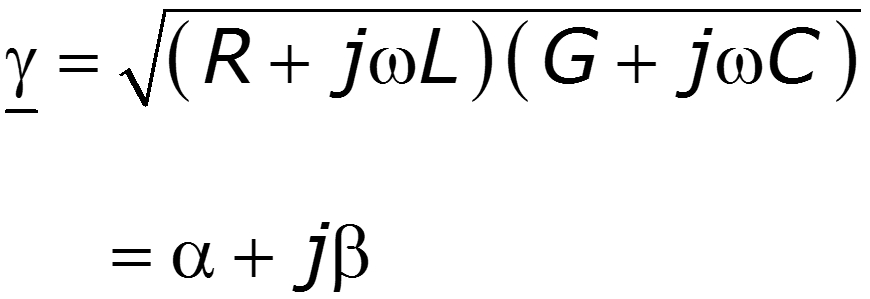
– коэффициент ослабления длинной линии [Нп/км], [Нп/м] или [ДБ/км], [ДБ/м];
Характеризует изменение тока и напряжения по абсолютной величине на единицу длины
- собственное ослабления линии [Нп] или [ДБ];
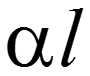
Ослабление сигнала на расстоянии х от начала линии
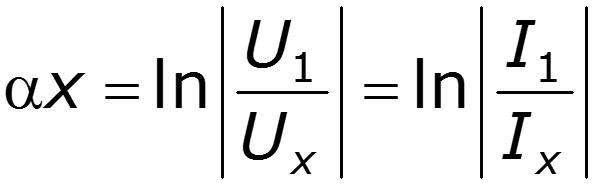
[Нп]
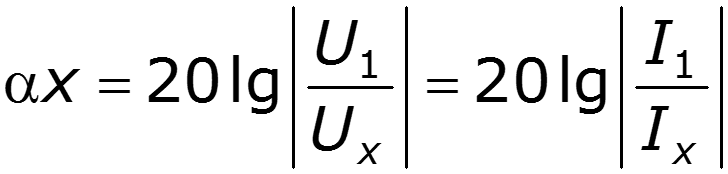
[ДБ]
– коэффициент фазы [рад/км], [рад/м], [градус/км], [градус/м].
Характеризует изменение тока и напряжения по фазе на единицу длины
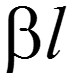
- собственная фаза линии [рад], [градус].
![]()
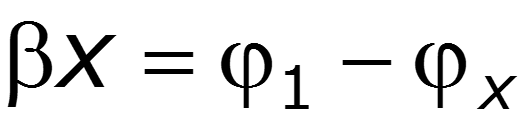
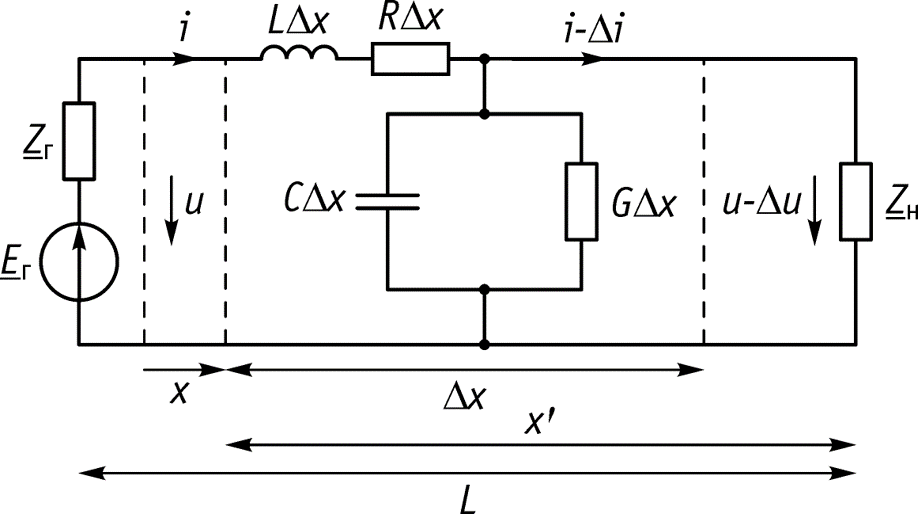
18.2 Уравнения передачи однородной линии
![]()
![]()
![]()
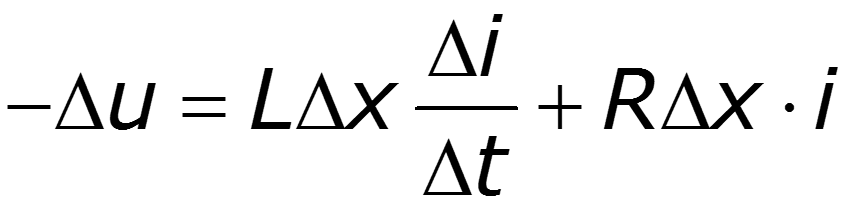
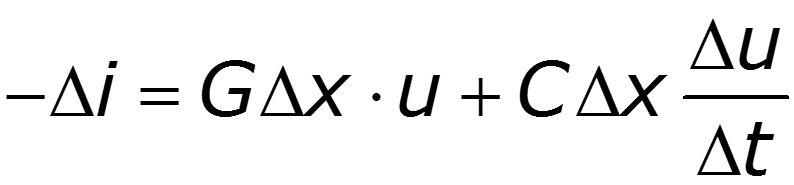
Телеграфные уравнения длинной линии
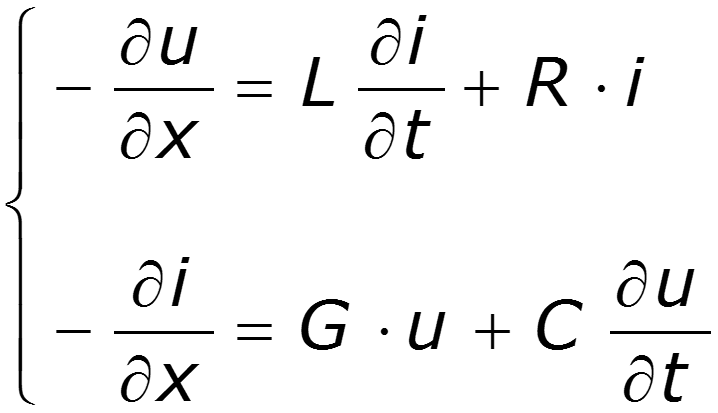
Для установившегося гармонического колебания телеграфные уравнения имеют вид
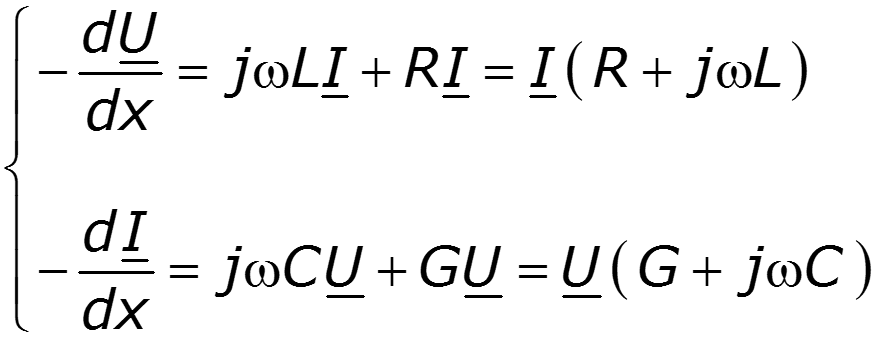
Для решения телеграфных уравнений необходимо разделить переменные (U и I). Для этого продифференцируем уравнения по х. В полученные уравнения подставим вместо и их выражения из системы уравнений для установившегося гармонического колебания
![]()
![]()
Волновые уравнения длинной линии
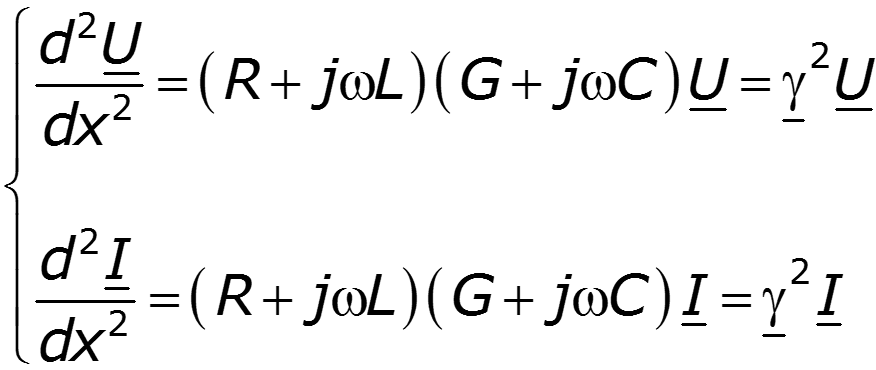
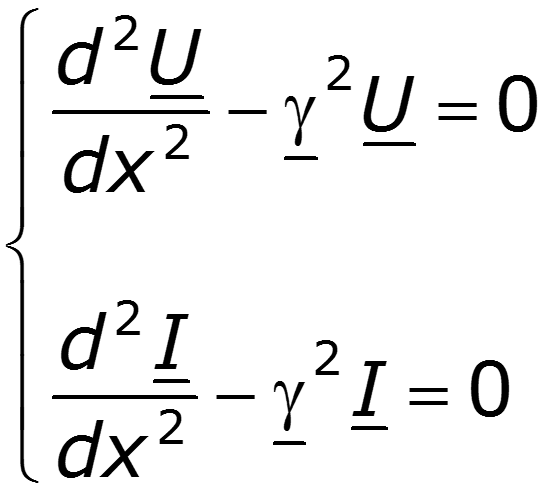
Поскольку волновые уравнения – линейные дифференциальные однородные уравнения 2-го порядка, то их решение в произвольном сечении х находится в виде
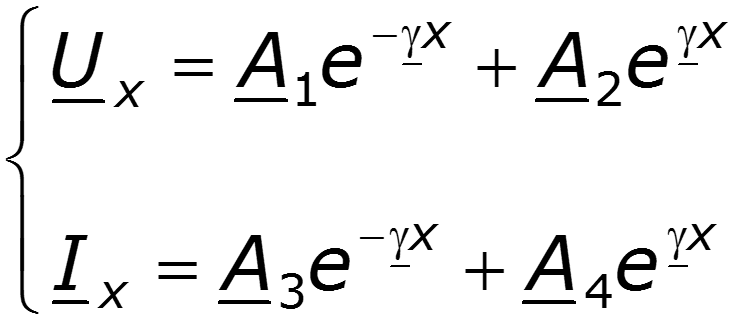
– постоянные интегрирования, определяемые из граничных условий, в качестве которых обычно используют напряжение и ток, либо в начале линии ( и при х = 0), либо ток и напряжение в конце линии ( и при х = ).
![]()
![]()
![]()
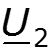
![]()
![]()
Решение для тока, как правило, выражают через найденное напряжение
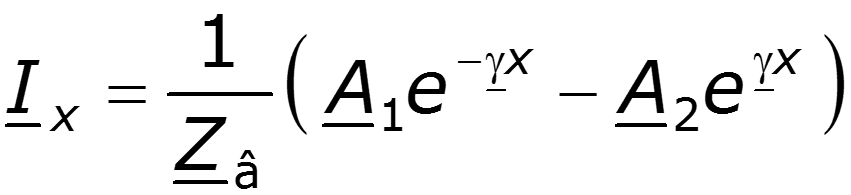
Определяем постоянные интегрирования из системы уравнений для напряжения и тока при x = 0
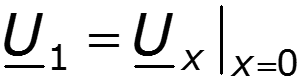
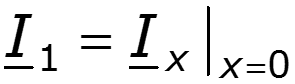
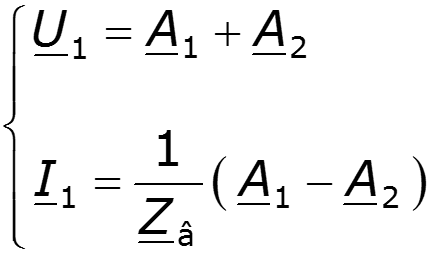
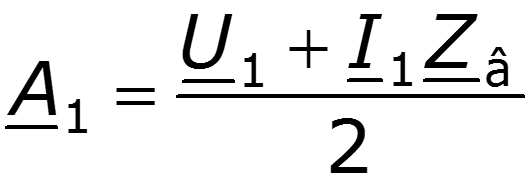
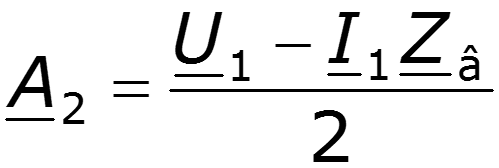
Уравнения передачи
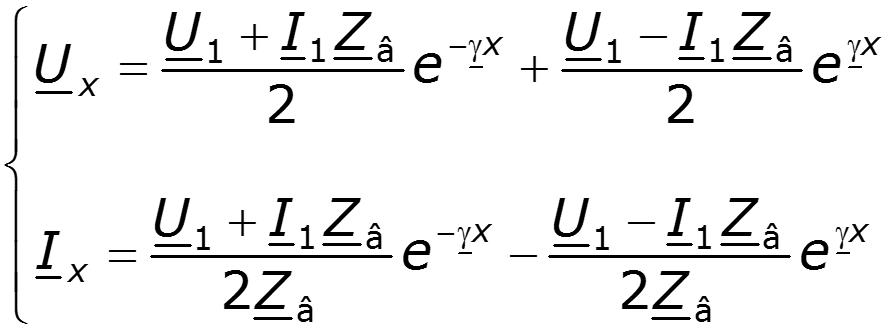
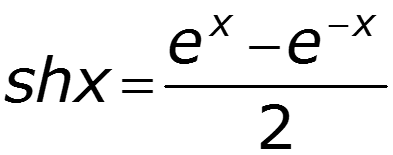

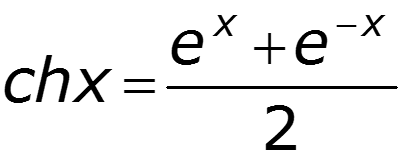
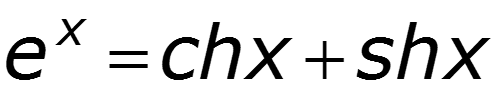
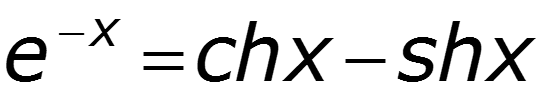
Уравнения передачи в гиперболической форме
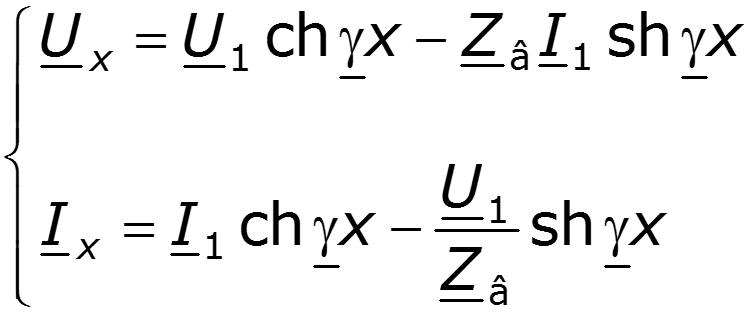
Уравнения передачи в начале линии , через напряжение и ток в конце линии
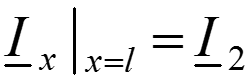
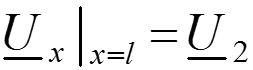
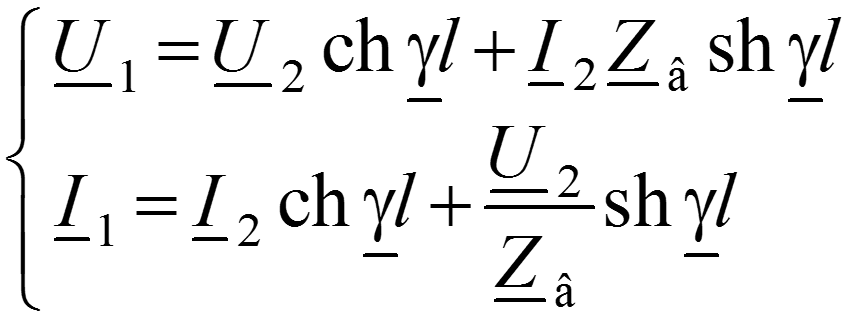
,
Уравнение передачи в конце линии , через напряжение и ток в начале линии
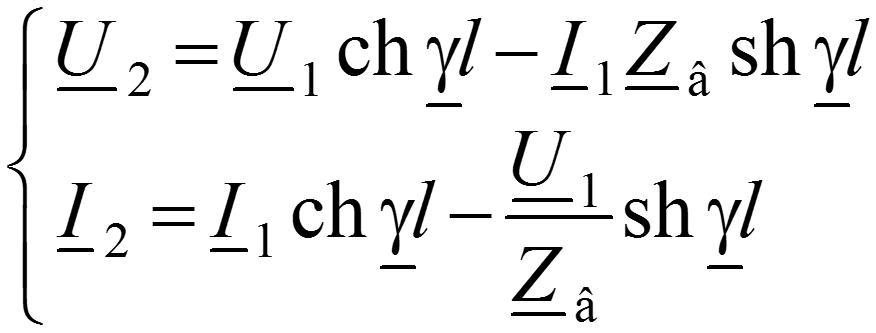
18.3 Волновые процессы в однородной длинной линии
В линиях с потерями ( 0) рассматривают бегущие затухающие прямые и обратные волны и их суперпозиции. Бегущая волна – волна, перемещающаяся вдоль линии.
Прямая бегущая волна – волна, перемещающаяся от начала к концу линии. Обратная бегущая волна – волна, перемещающаяся от конца к началу линии
Падающая волна – прямая бегущая волна. Отраженная волна – частный случай обратной бегущей волны, возникающей в результате неравенства волнового сопротивления линии и сопротивления нагрузки ( ).
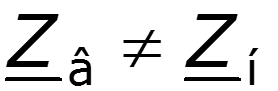
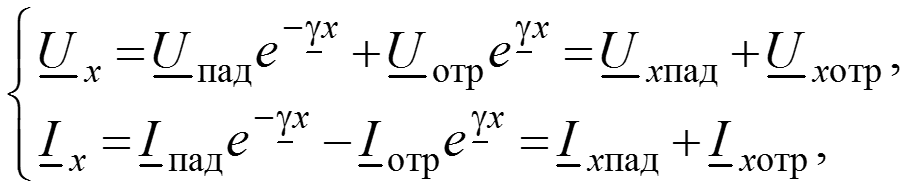
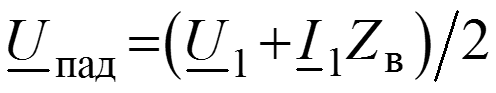
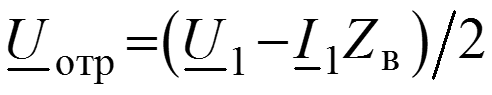
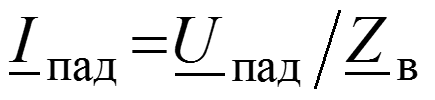
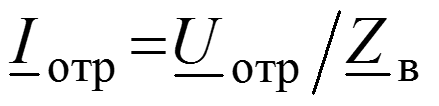
Уравнения передачи для мгновенных значений в любом сечении
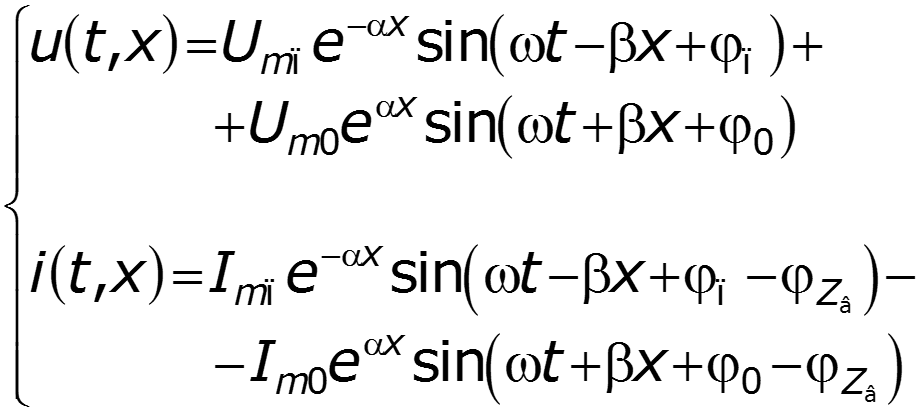
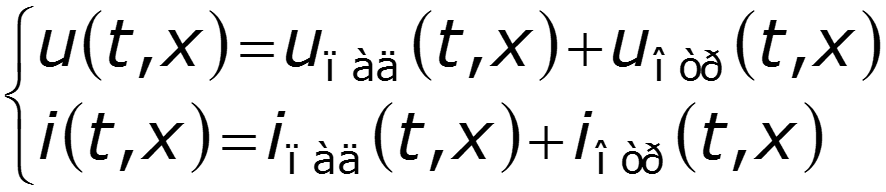
Соотношения между волнами в начале (x = 0) и в конце (x = l) линии
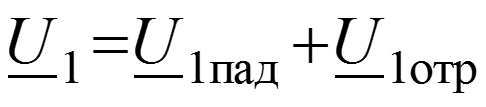
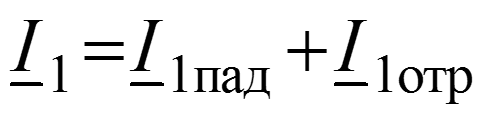
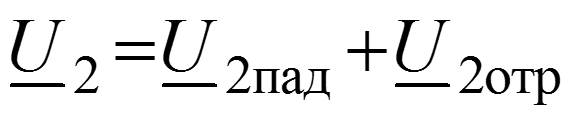
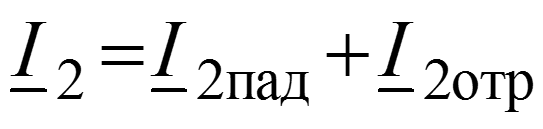
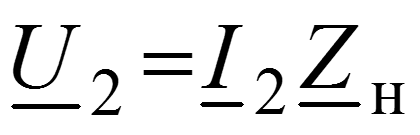
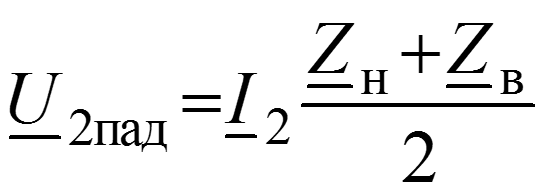
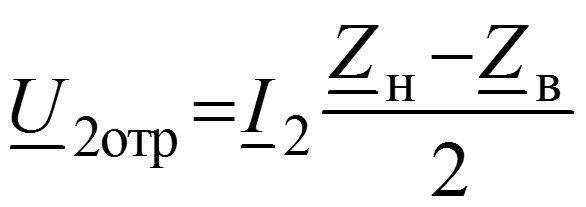
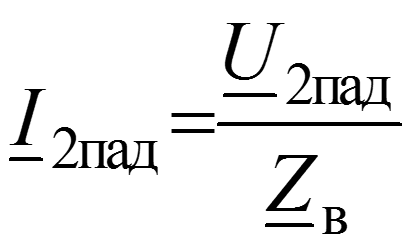
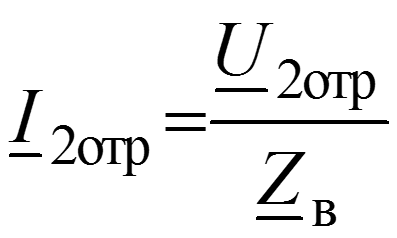
Длина волны – расстояние между ближайшими точками х1 и х2, взятое в направлении распространения волны, фазы колебания в которых отличаются на 2.

Фазовая скорость – скорость перемещения фазы колебания
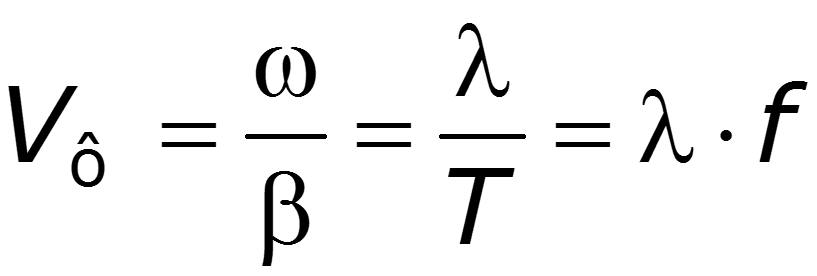
За один период колебания бегущая волна проходит расстояние, равное длине волны
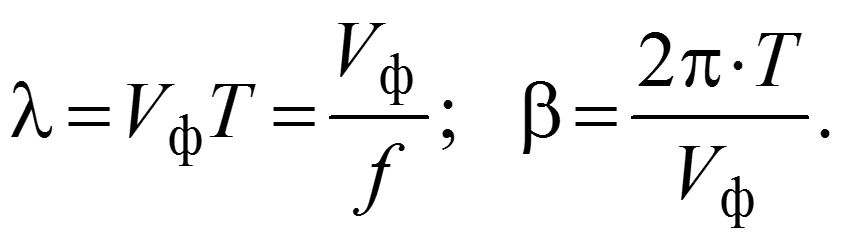
Коэффициент отражения по напряжению (току) –отношение комплексной амплитуды отраженной волны напряжения (тока) к комплексной амплитуде падающей волны напряжения (тока).
показывает, какую часть комплексной амплитуды падающей волны составляет комплексная амплитуда отраженной волны
Коэффициенты отражения по напряжению и по току в начале линии
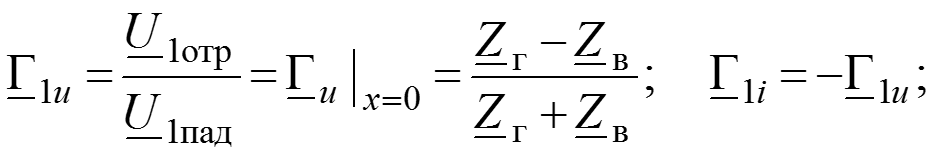
Коэффициенты отражения по напряжению и по току в конце линии
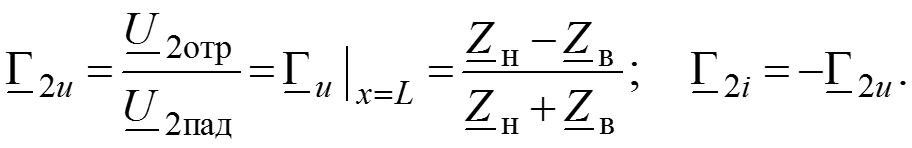
Режим согласованного включения
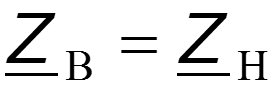
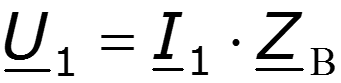
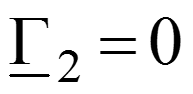
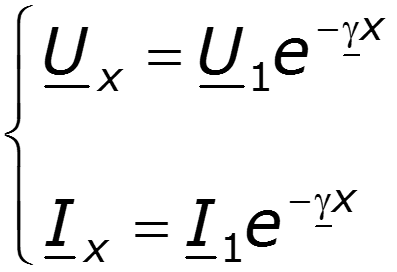
Линия без искажений
Линия, на приемном конце которой сохраняется форма передаваемого сигнала
Для такой передачи необходимо:

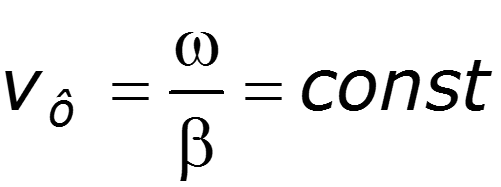
2. 3. Линия согласованно нагружена
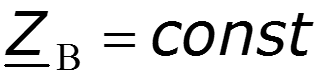
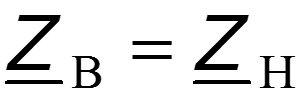
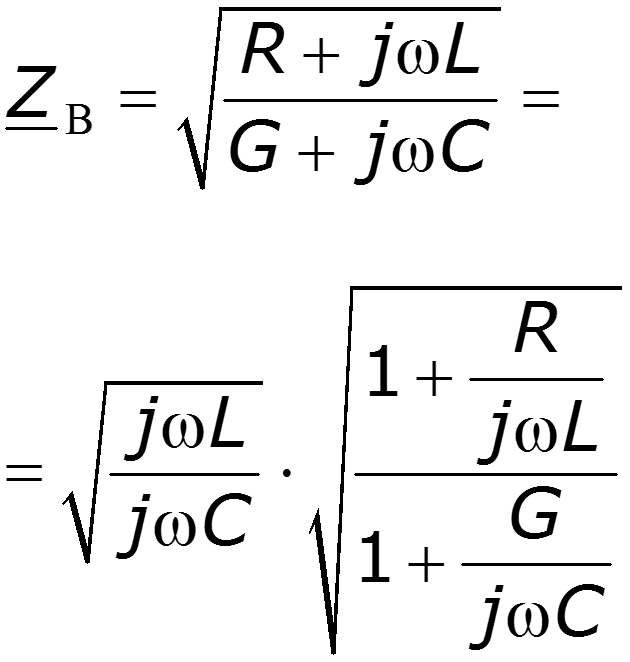
Подберем первичные параметры так, чтобы - условие Хевисайда
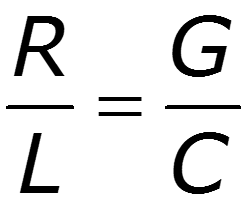
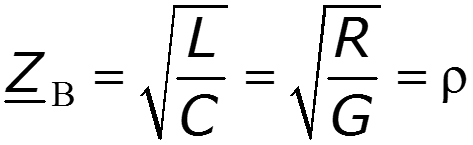
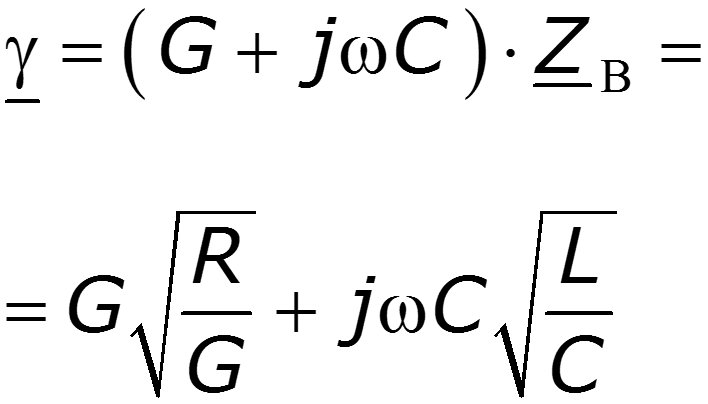
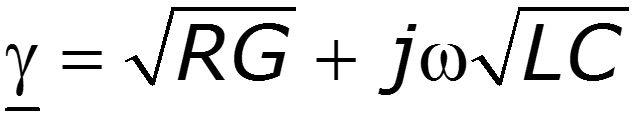
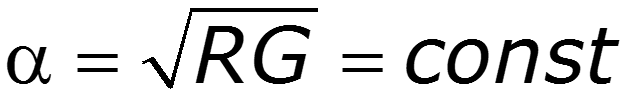
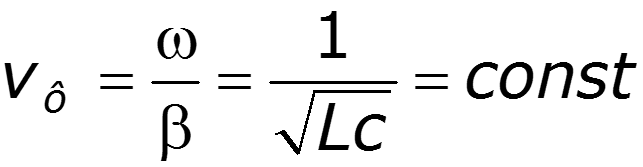
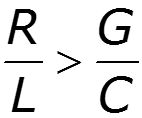
Для реальных линий обычно
Уменьшение R – увеличение диаметра провода (дорого)
Уменьшение С – увеличение расстояния между проводами (не всегда возможно)
Увеличение G – рост затухания
Лучше всего – искусственное увеличение L
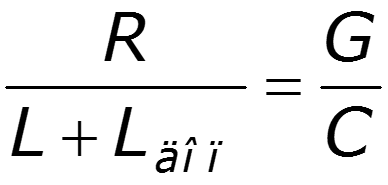
При передаче ВЧ сигнала автоматически получается линия без искажений
18.4 Волновые процессы длинной линии без потерь
Такая линия, для которой (для небольших линий на СВЧ)
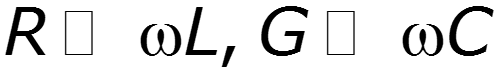
тогда
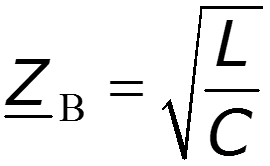
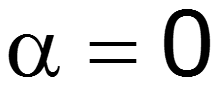
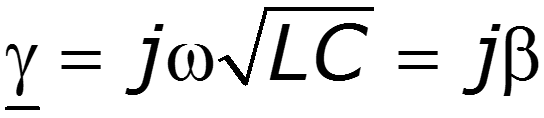
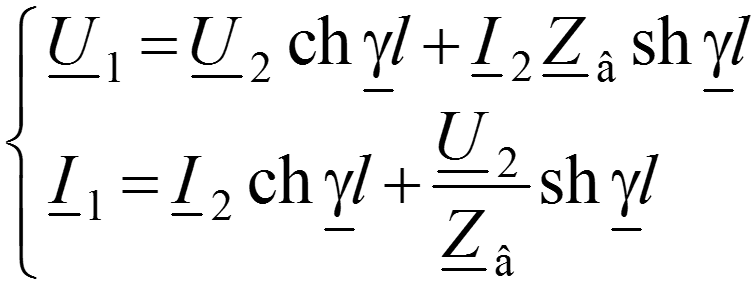
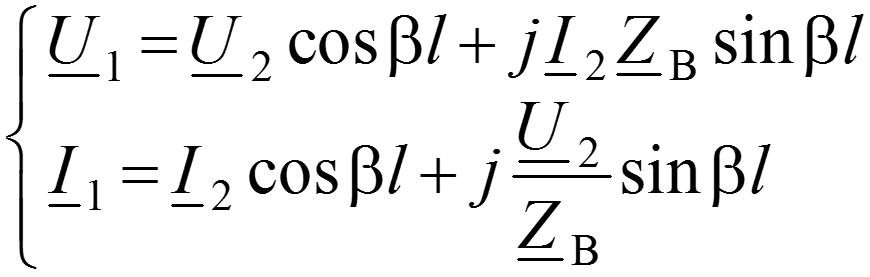
Входное сопротивление линии
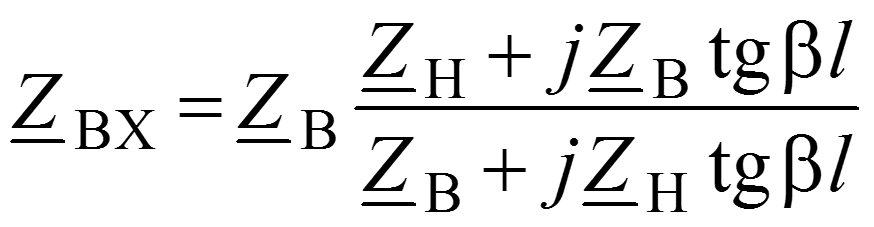
1. Согласованный режим работы в длинной линии без потерь
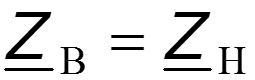
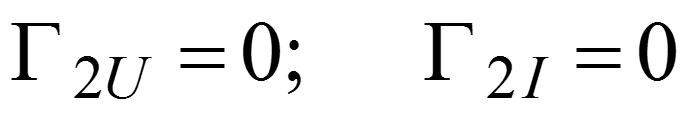
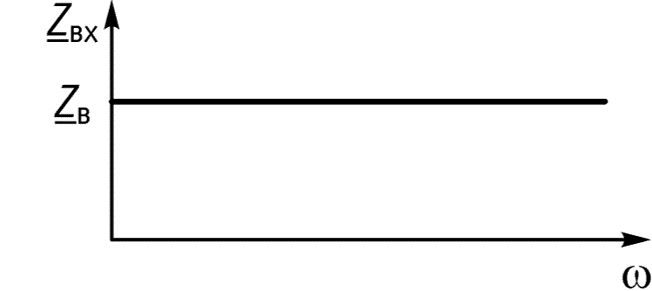
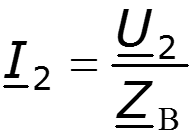
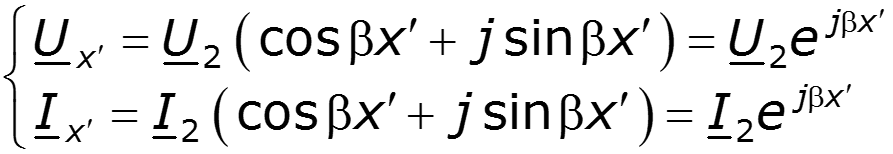
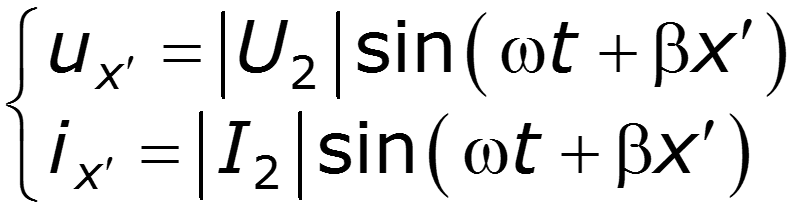
Режим бегущей волны
2. Режим короткого замыкания
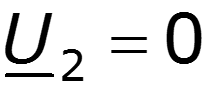
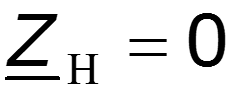
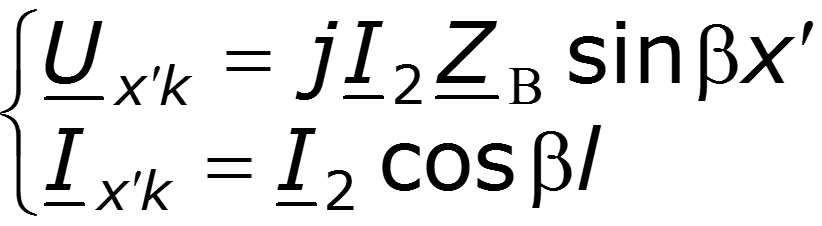
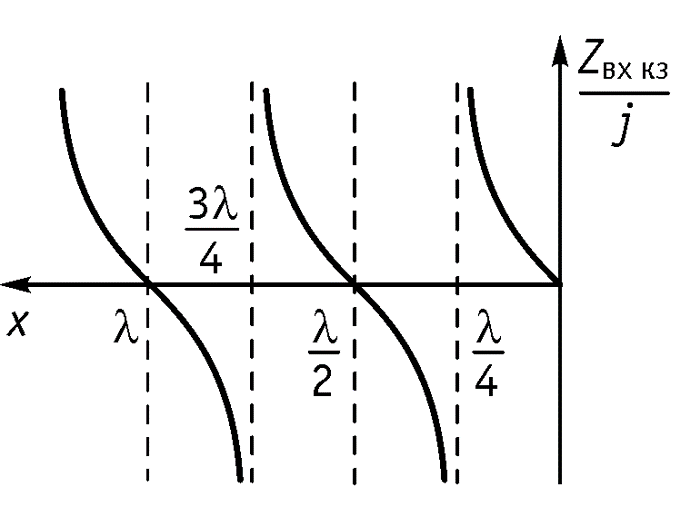
Уравнение стоячей волны
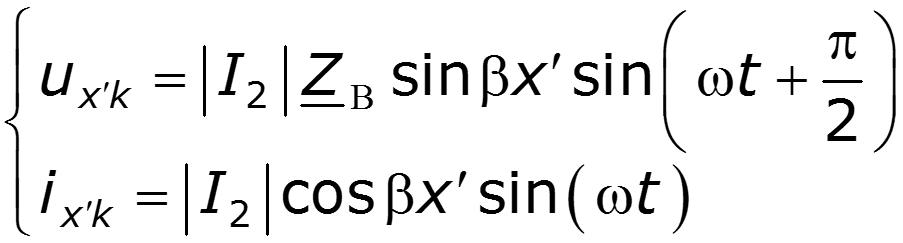
Амплитуды напряжения и тока являются функциями координаты х
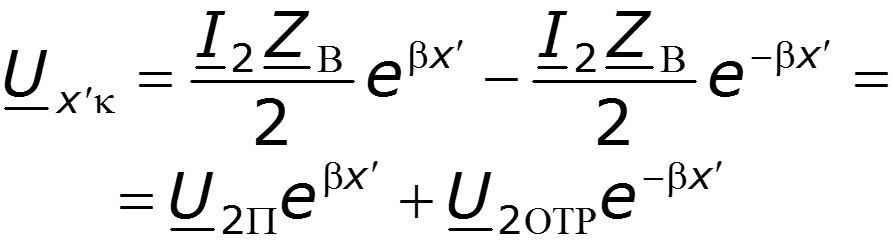
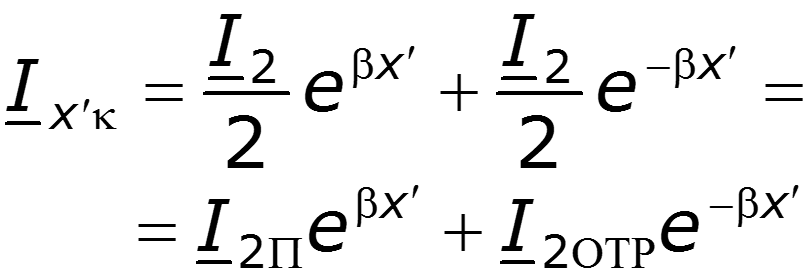
Нулевое значение – узел стоячей волны Максимальное значение – пучность стоячей волны
Стоячие волны возникают в длинной линии без потерь при условии, когда к длинной линии подключена нагрузка, модуль коэффициента отражения которой равен 1, при этом амплитуды падающей и отраженной волн напряжения (тока) переносят одинаковую мощность в прямом и обратном направлениях и энергия в нагрузке не потребляется.
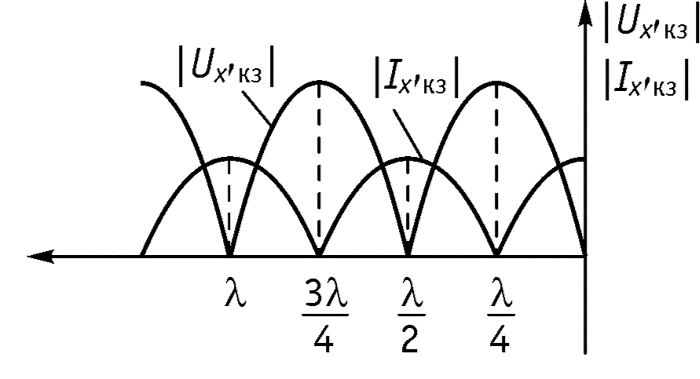
3. Режим холостого хода
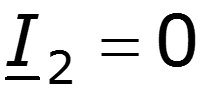
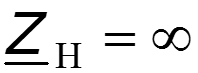
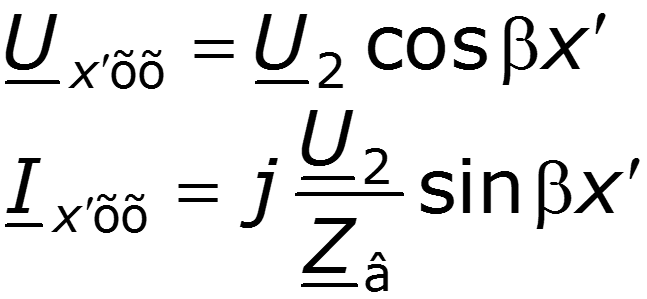
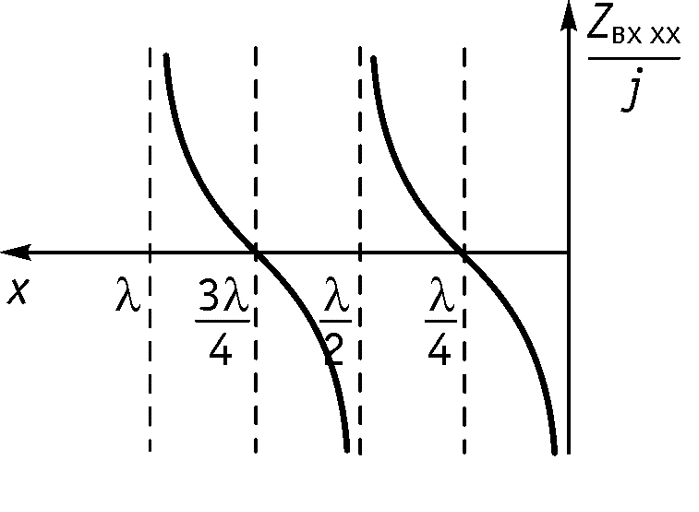
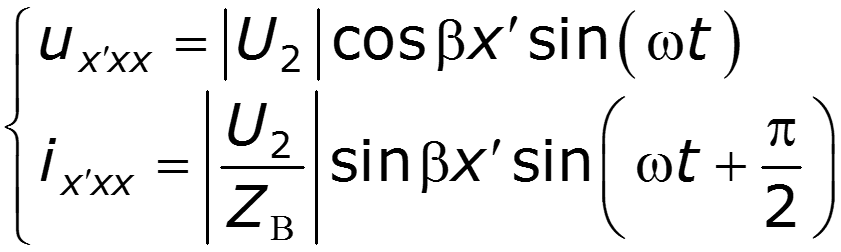
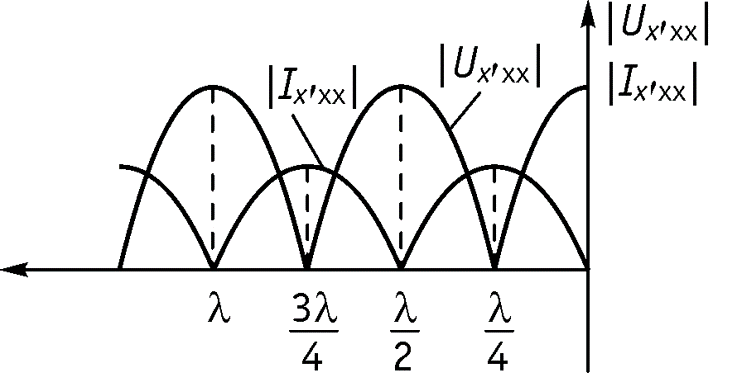
4. Линия, нагруженная на активное сопротивление, не равное волновому
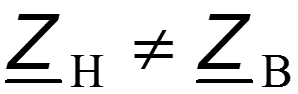
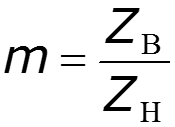
- режим смешанных волн
Коэффициент бегущей волны
используется для оценки близости смешанной волны к режиму бегущей волны
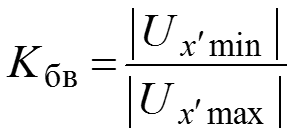
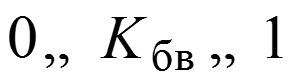
Если , то в линии наступает режим стоячей волны, если , то в линии наступает режим бегущей волны.
![]()
![]()
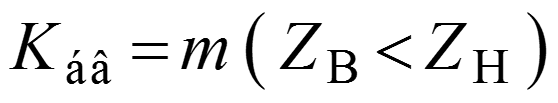
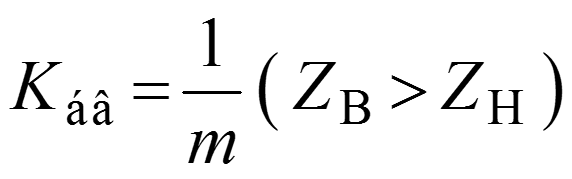
Коэффициент стоячей волны
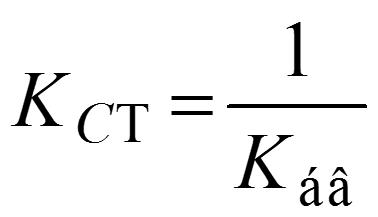
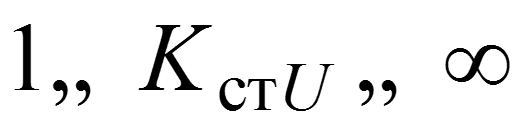
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.