- амплитуда колебания, приходящаяся на 1 Гц в бесконечно узкой полосе частот, включающей в себя рассматриваемую частоту
Физический смысл обратного преобразования Фурье
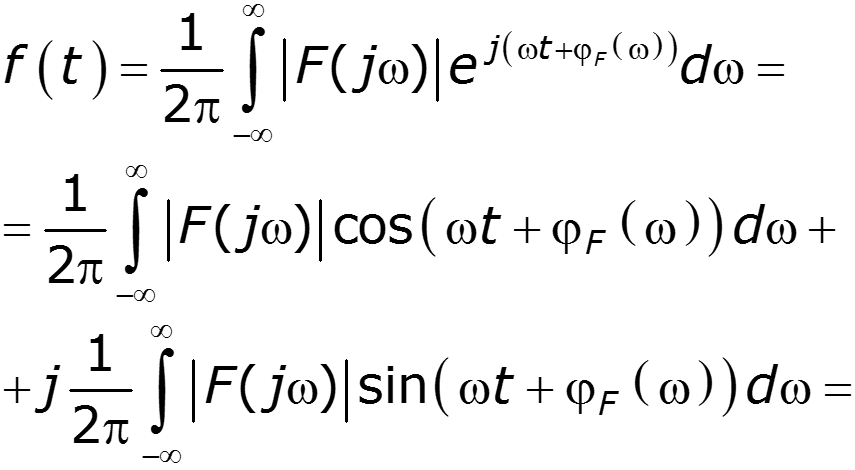
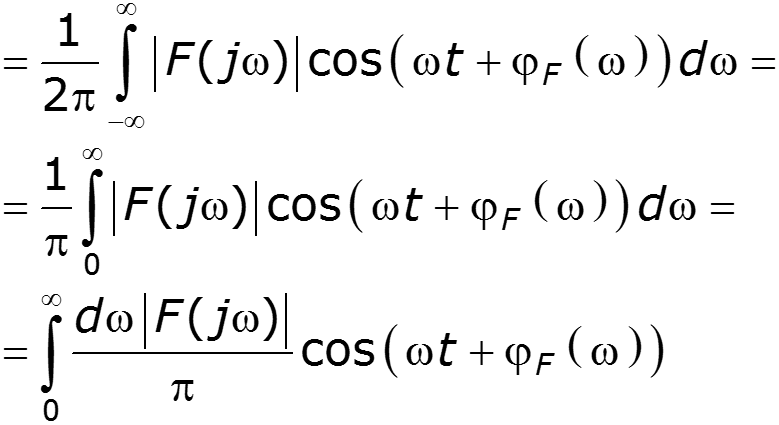
сигнал можно представить в виде суммы бесконечного количества гармонических составляющих с бесконечно малыми амплитудами
Основные свойства преобразования Фурье
1. Если функция четная, то спектр – вещественная величина
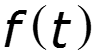

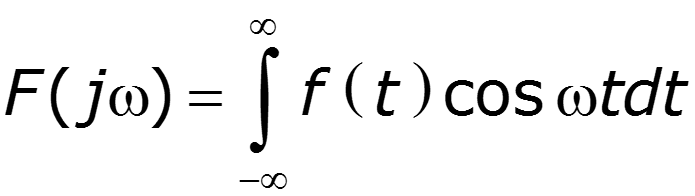
2. Если функция нечетная, то спектр –мнимая величина 3. Если функция четная, то справедлива формула
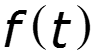
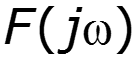
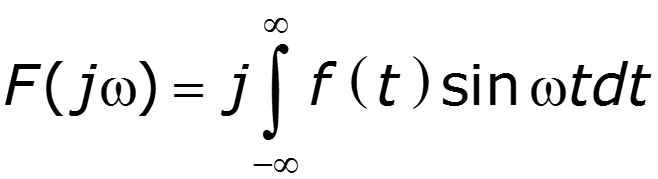
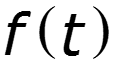
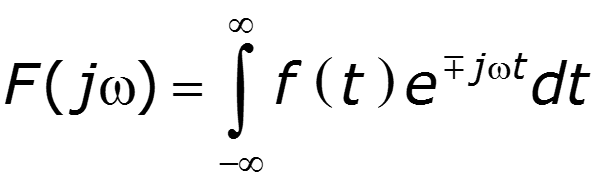
4. Свойство взаимозаменяемости переменной и t
![]()
Для четного сигнала и вещественного спектра
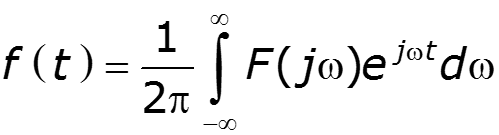
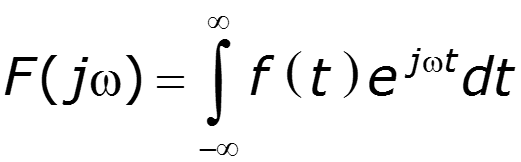
позволяет установить связь между временными и частотными характеристиками сигнала
5. Однозначная связь между мнимой и действительной частями спектра 6. На нулевой частоте спектр равен площади, ограниченной сигналом
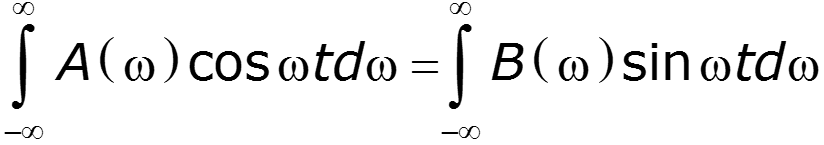
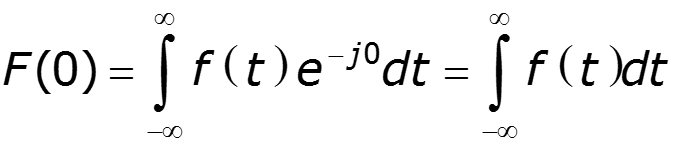
9.6 Спектр прямоугольного импульса
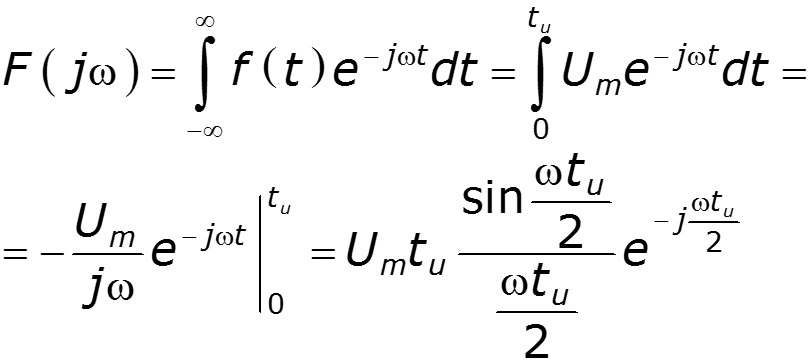
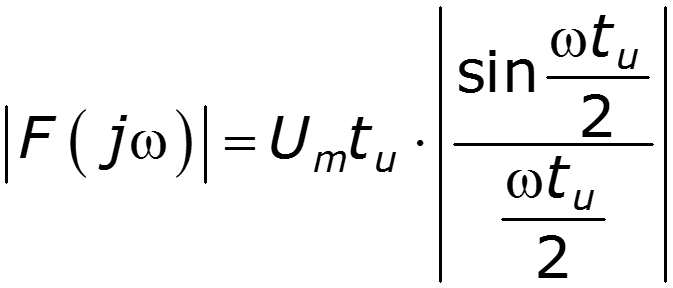
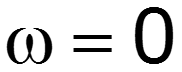
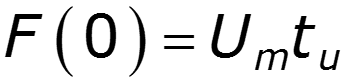
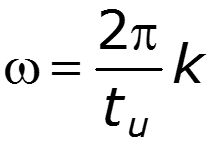
нули
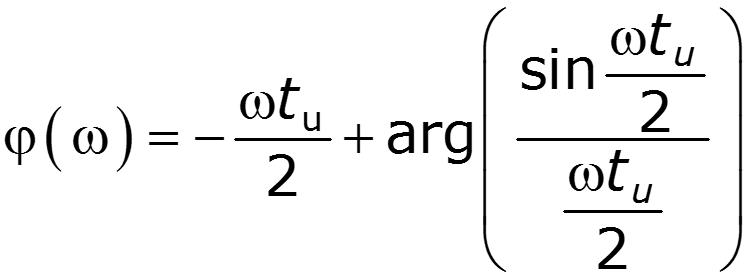
Чтобы получить дискретный спектр периодического сигнала, нужно заменить в выражении для спектральной плотности непериодического сигнала частоту на Тогда
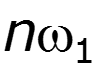
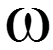
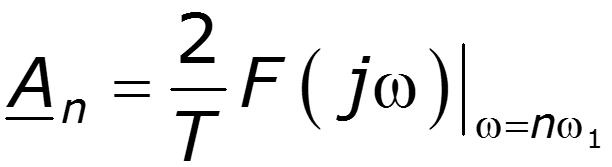
9.7 Одностороннее преобразование Фурье. Связь с преобразованием Лапласа
Если при
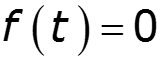
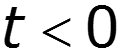
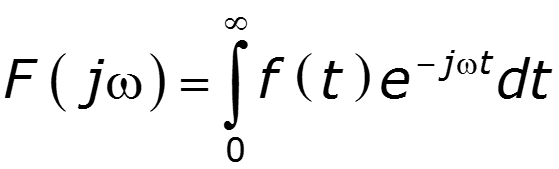
Одностороннее преобразование Фурье
Преобразования Лапласа
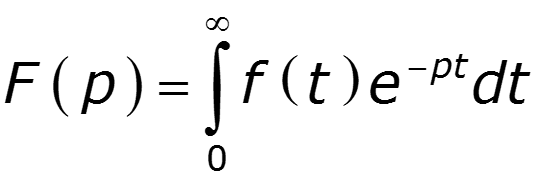
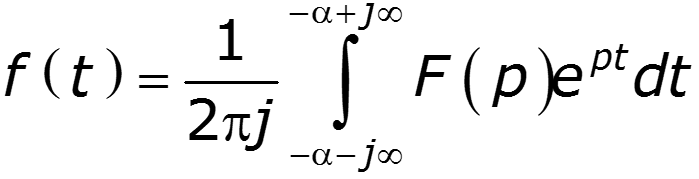
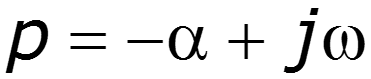
при
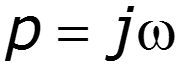
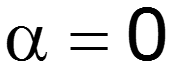
Преобразование Лапласа
Преобразование Фурье
![]()
Для определения спектра сигнала можно использовать преобразование Лапласа
1) Спектр импульса включения
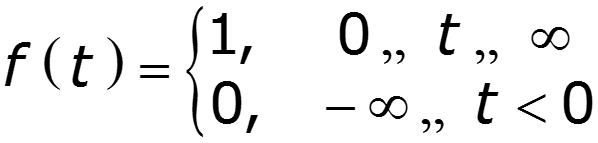
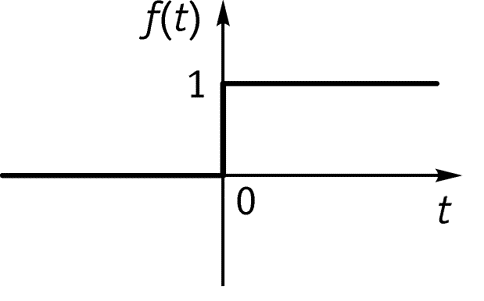
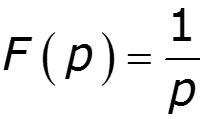
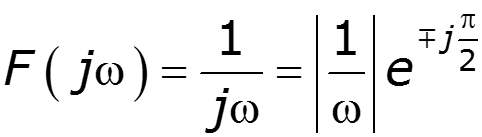
2) Спектр синусоидального импульса включения
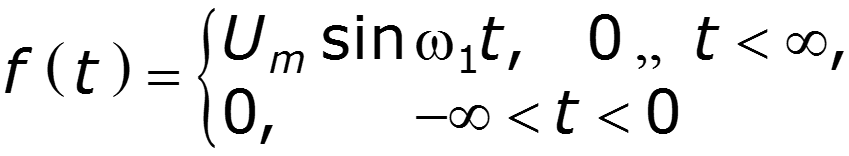
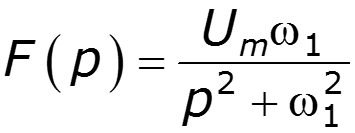
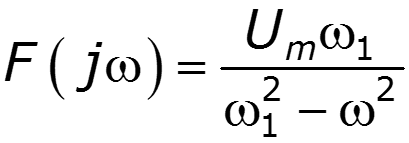
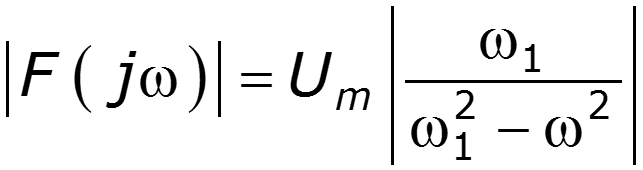
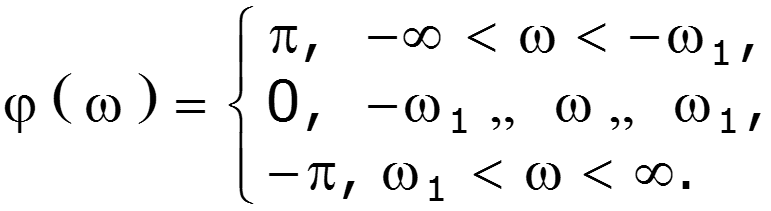
3) Спектр -импульса
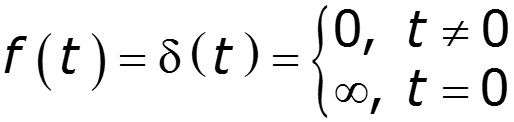
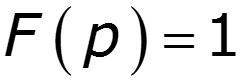
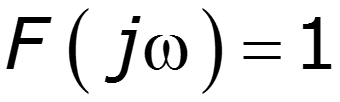
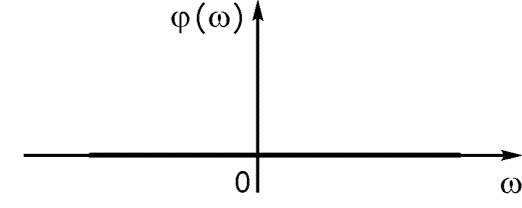
4) Спектр экспоненциального импульса
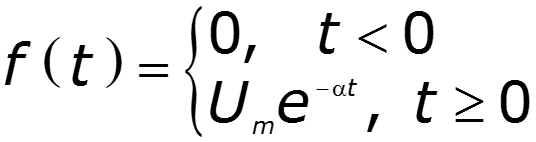
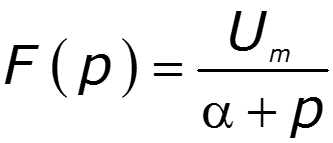
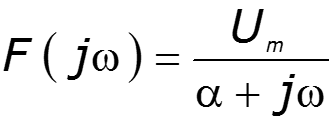
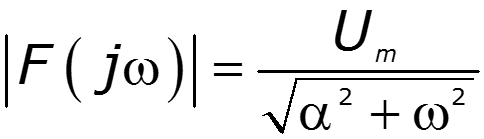
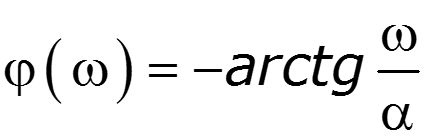
9.8 Теоремы о спектрах
1. Теорема линейности
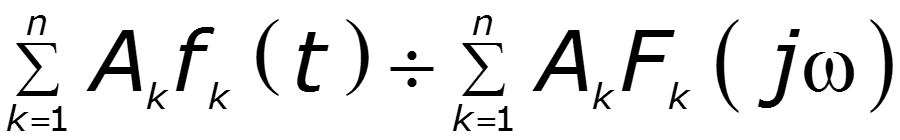
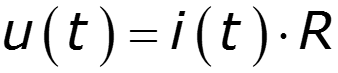
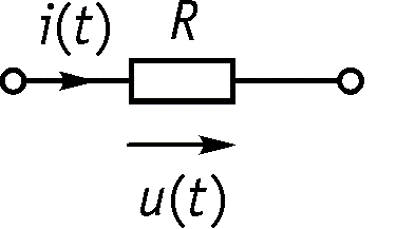
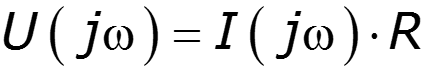
Законы Кирхгофа
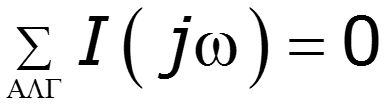
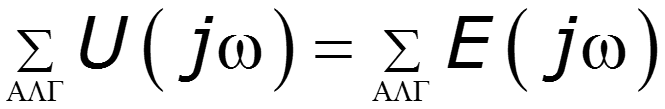
2. Теорема дифференцирования
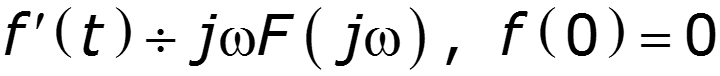
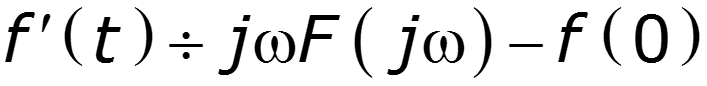
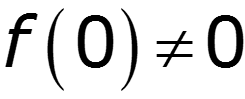
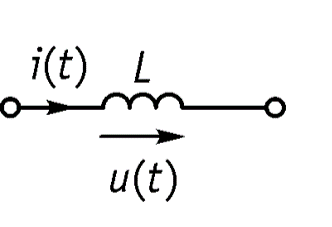
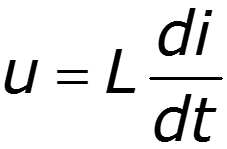
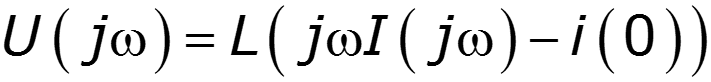
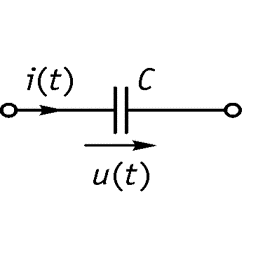
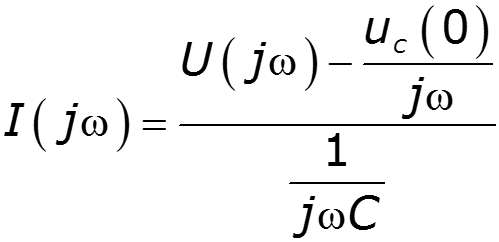
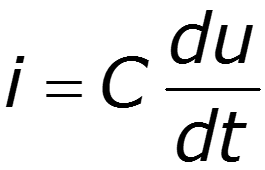
Дифференцирование сигнала ведет к расширению его спектра
3. Теорема интегрирования
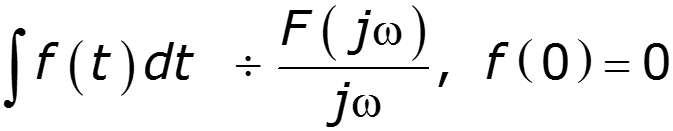
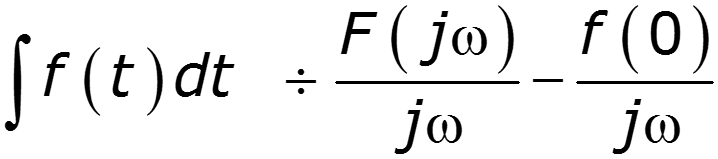
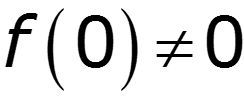
Интегрирование сигнала ведет к сужению его спектра
4. Теорема подобия
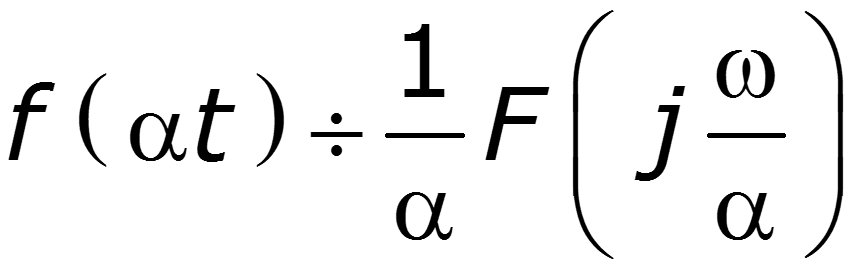
Чем короче импульс, тем шире его спектр
5. Теорема запаздывания Спектральная плотность амплитуд не меняется, меняется только спектральная плотность фаз
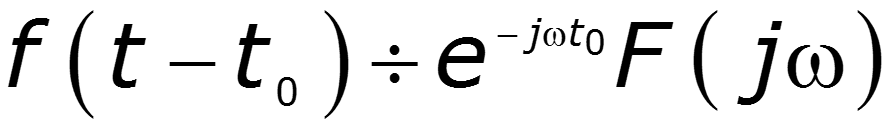
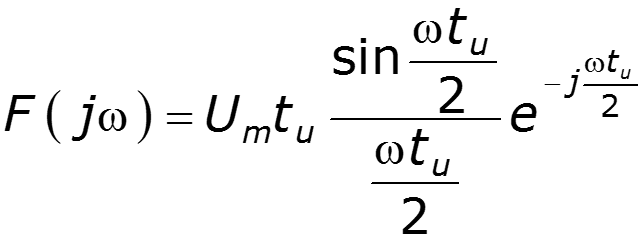
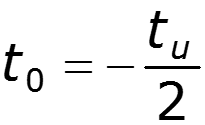
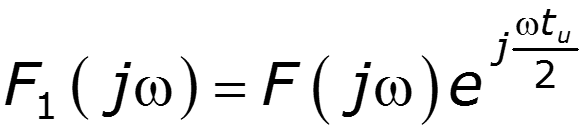
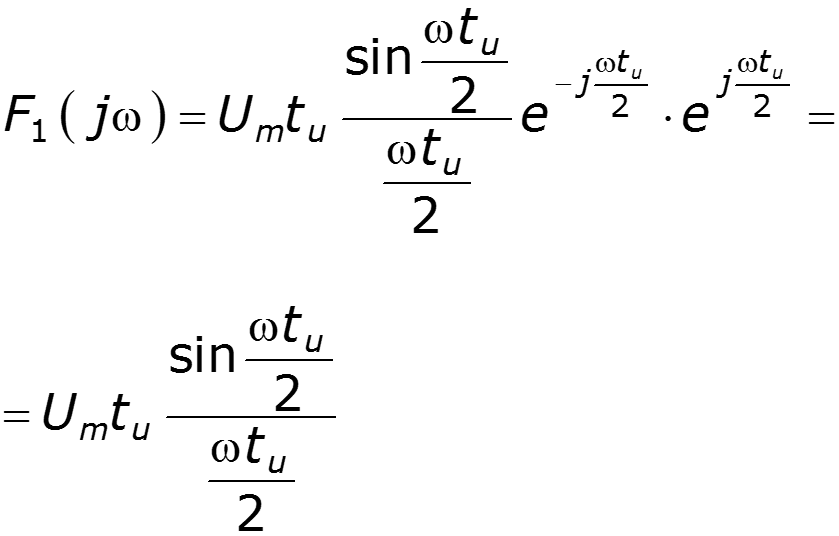
6. Теорема смещения
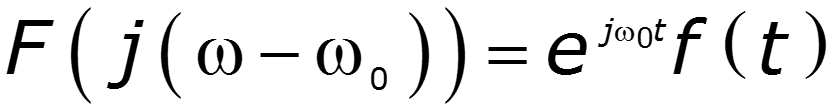
видеоимпульс радиоимпульс
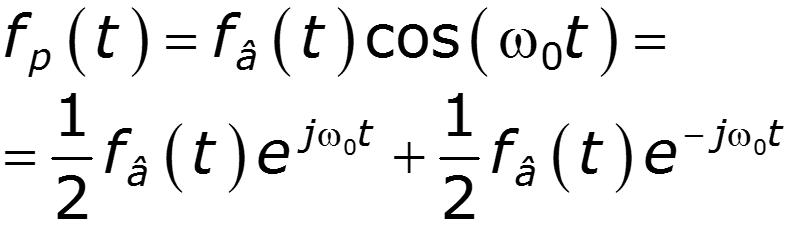
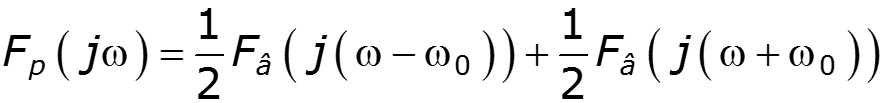
7. Теорема свертки
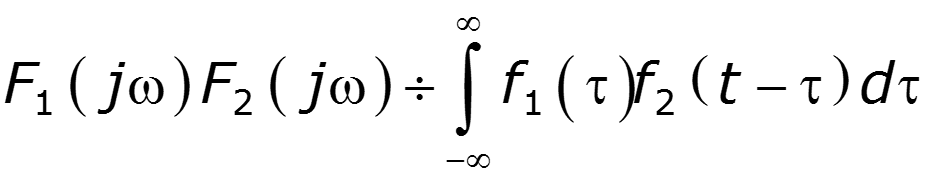
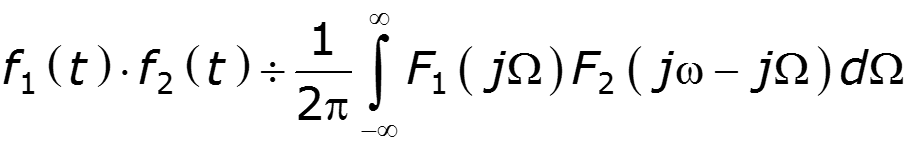
8. Равенство Парсеваля (теорема Релея)
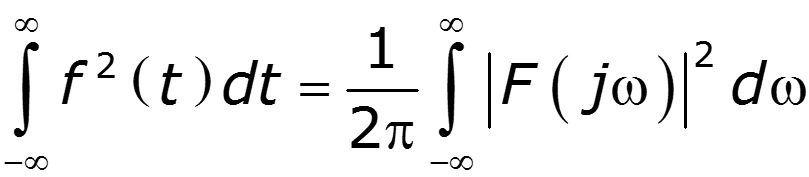
Энергия сигнала во временной области равна энергии сигнала в частотной области
- энергия электрического сигнала, рассеиваемая на сопротивлении R=1 Ом спектральная плотность энергии сигнала – энергетический спектр – показывает, какая доля энергии заключена в каждой полоске частот шириной в окрестности частоты
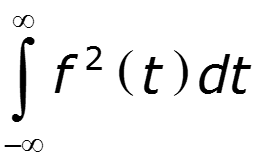
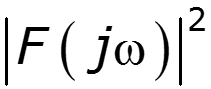
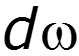
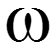
позволяет судить об распределении энергии в спектре непериодического сигнала
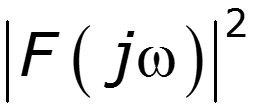
Равенство Парсеваля применяют для выбора полосы пропускания канала
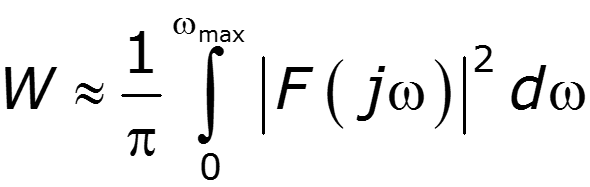
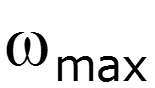
выбирают из условия передачи 90% энергии сигнала
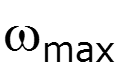
Найдем для прямоугольного импульса
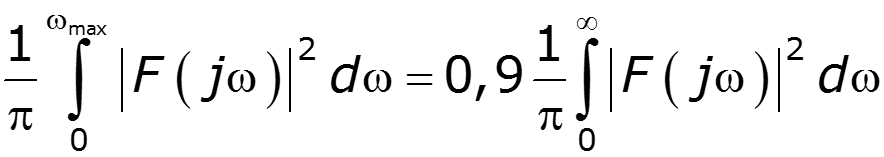
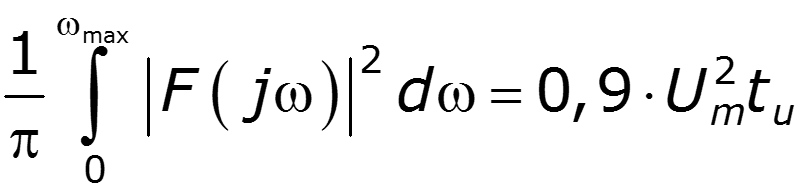
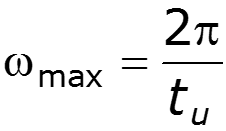
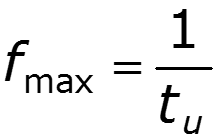

Пример
Найти спектр сигнала U2, если задан спектр сигнала U1
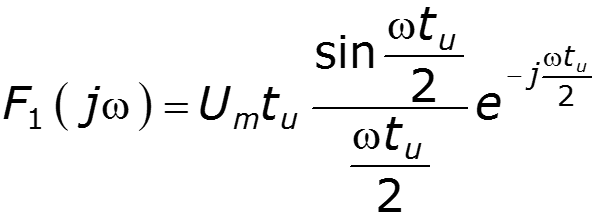
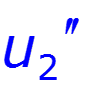
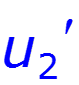
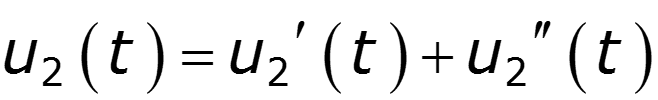
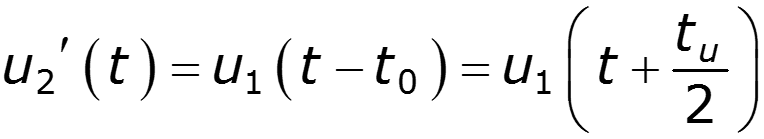
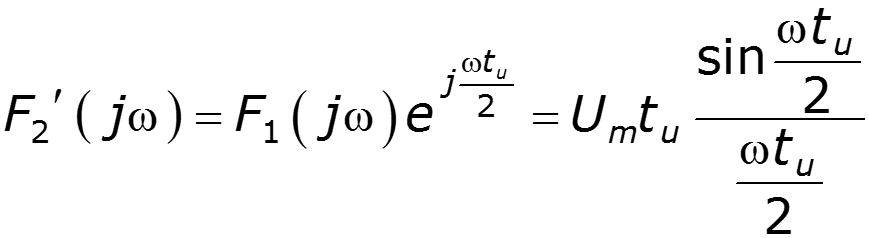
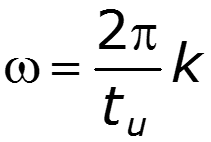
нули
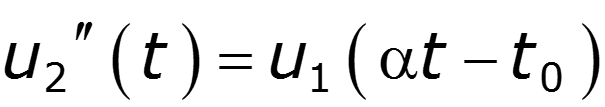
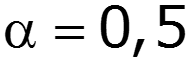
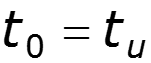
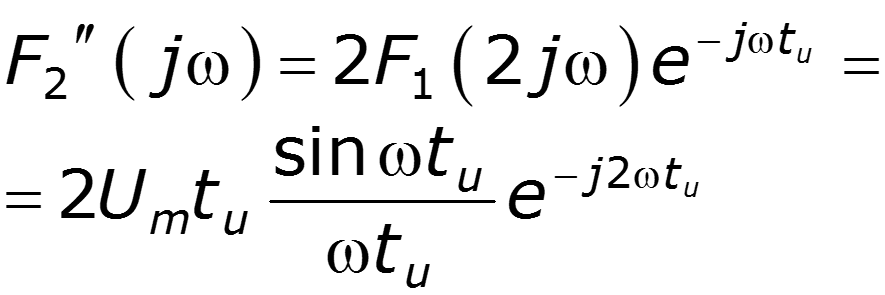
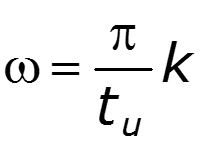
нули
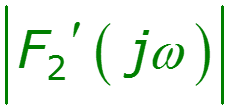
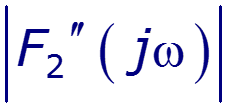

Пример
Найти спектр прямоугольного импульса, используя преобразование Лапласа и теоремы о спектрах
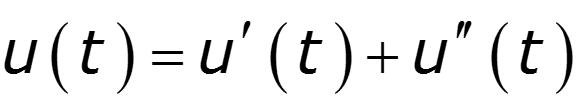
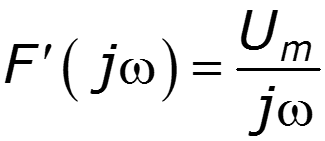
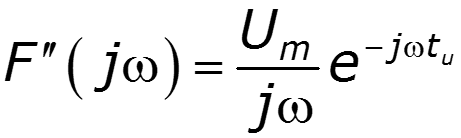
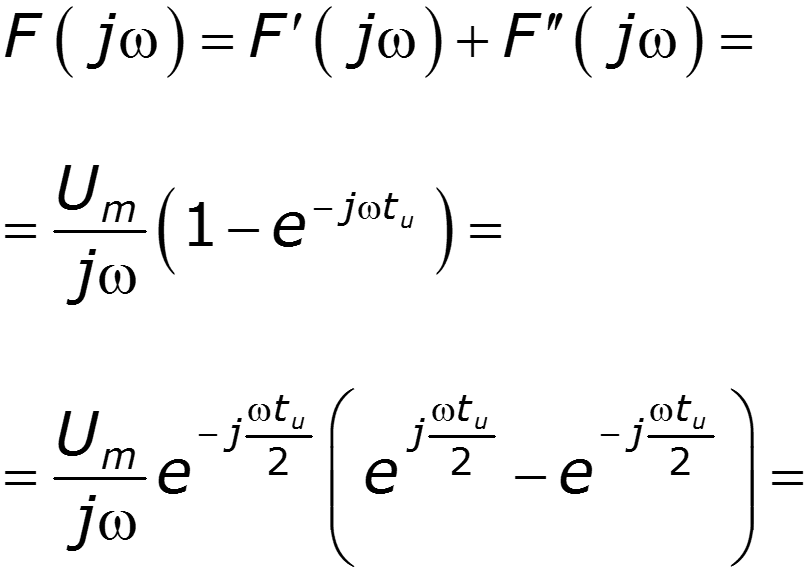
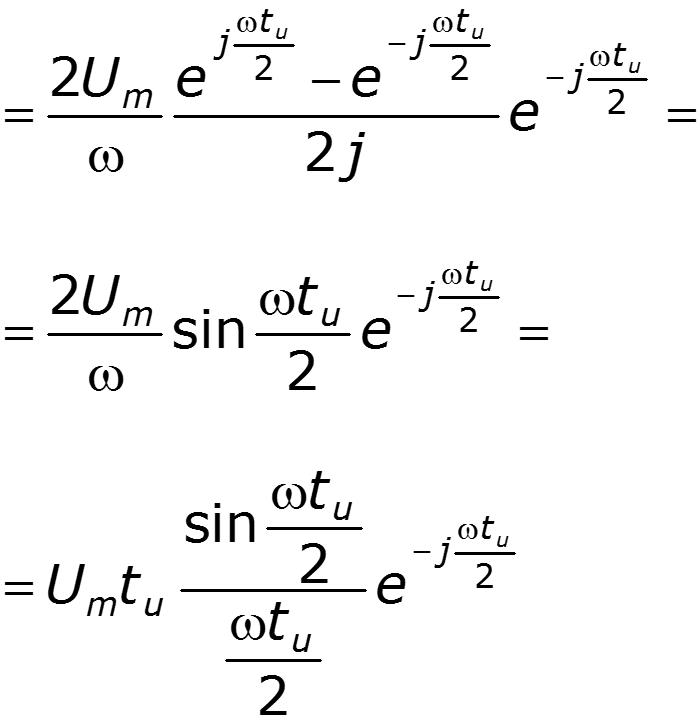
Пример
Найти спектральную плотность сигнала
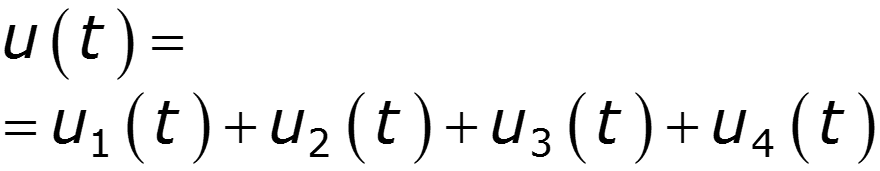
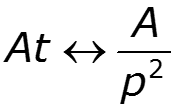
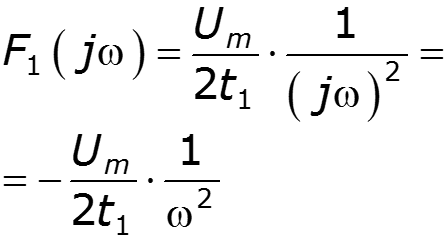
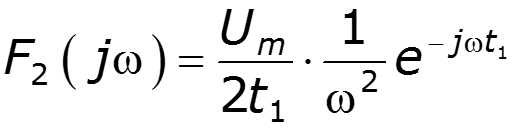
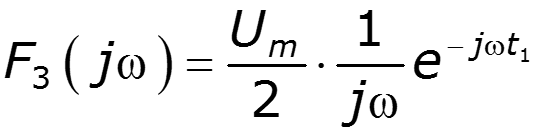
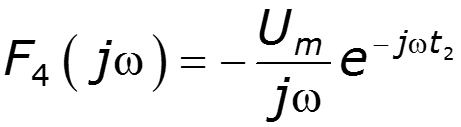
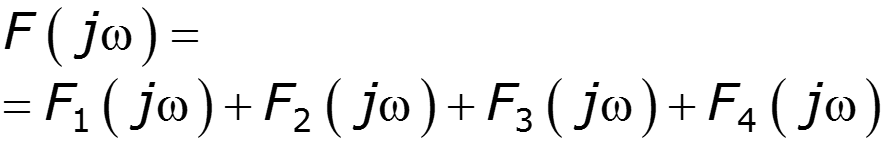
9.9 Спектральный метод расчета электрических цепей
В основе – использование КПФ цепи
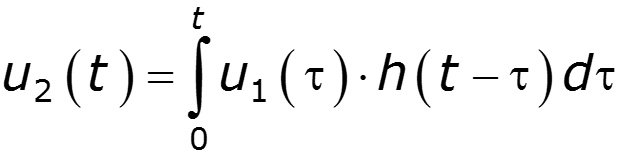
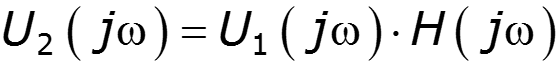
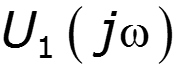
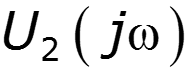
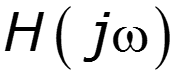
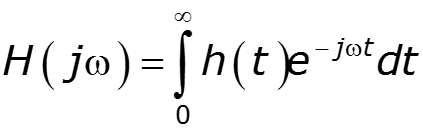
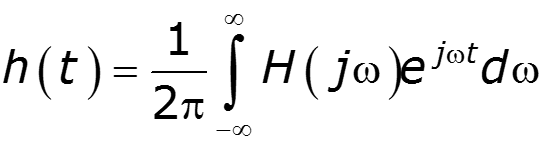
- определяет цепь в частотной области - определяет цепь во временной области
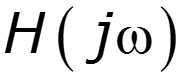
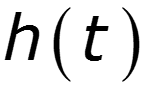
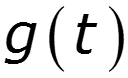
Предельные соотношения между и
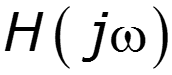
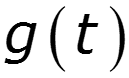
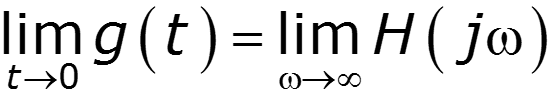
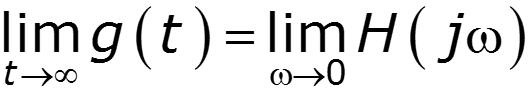
![]()
![]()
![]()
![]()
![]()
пример
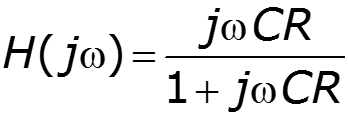
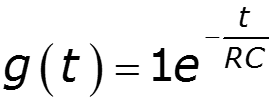
Порядок расчета цепей спектральным методом
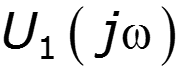
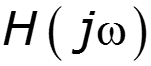
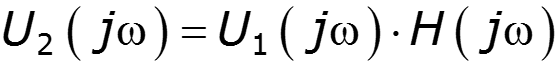
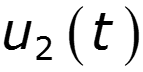
Определения сигнала по его спектральной плотности
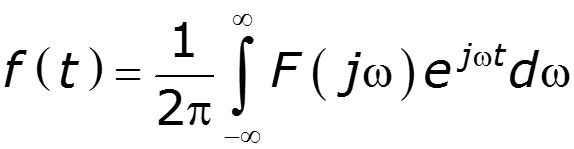
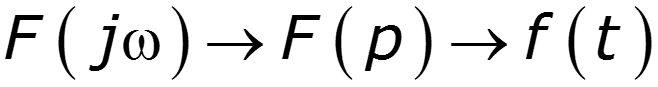
Пример
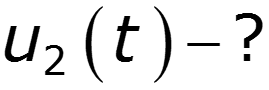
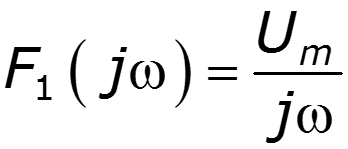
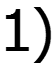
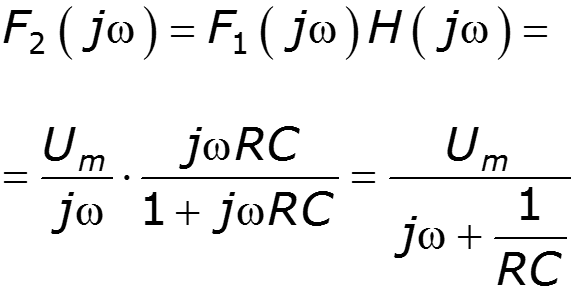
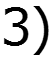
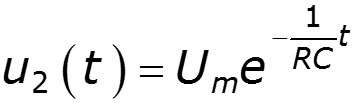

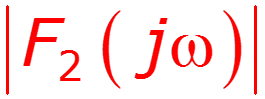
9.10 Условия безыскаженной передачи сигналов через линейную электрическую цепь
Условие безыскаженной передачи
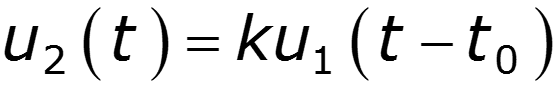
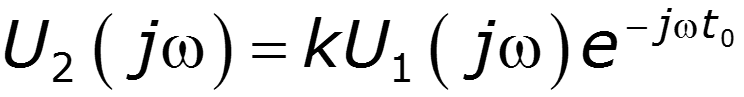
Комплексная передаточная функция неискажающей цепи
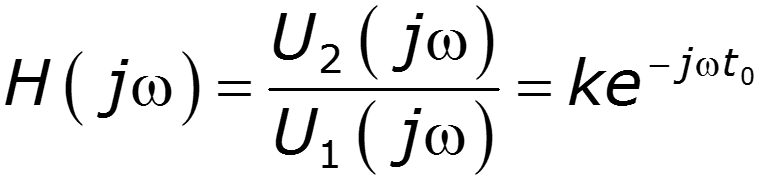
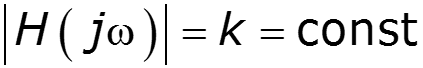
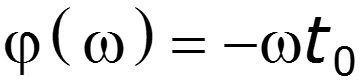
Условие безыскаженной передачи во всем частотном диапазоне можно выполнить лишь для резистивных цепей. В цепях с реактивными элементами условия безыскаженной передачи сигнала можно обеспечить лишь в ограниченном диапазоне частот.
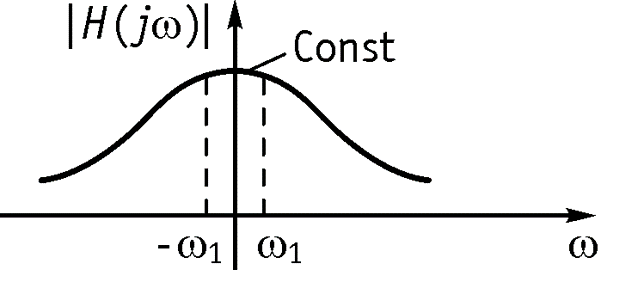
Если входной сигнал имеет спектр больше диапазона частот безыскаженной передачи, то это приводит к линейным частотным искажениям сигнала
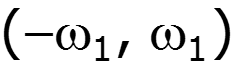
Прохождение сигналов через электрическую цепь
Пусть дана цепь с КПФ, соответствующей идеальному фильтру нижних частот
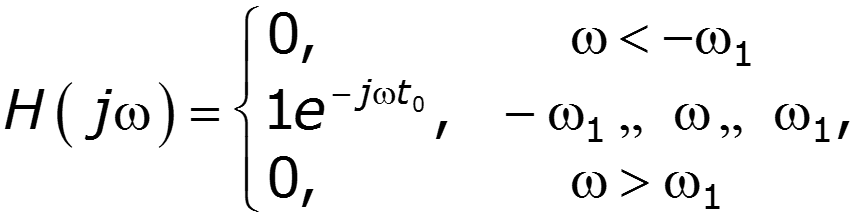
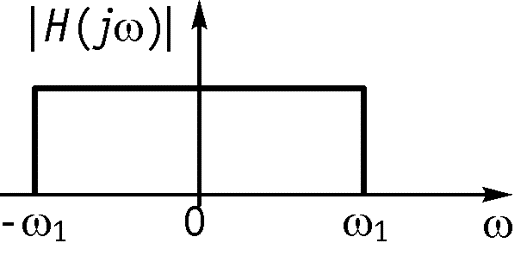
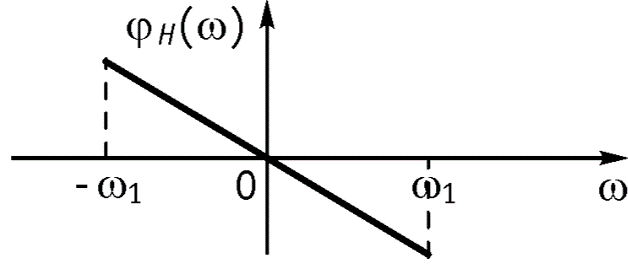
1.Прохождение -функции через идеальный ФНЧ
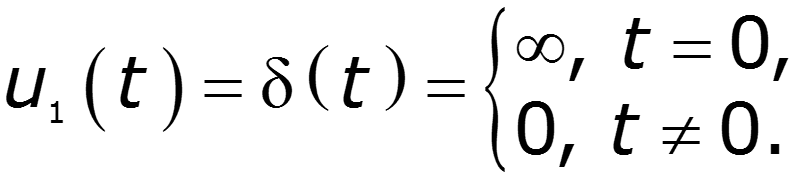
Спектральная плотность входного сигнала Спектральная плотность выходного сигнала
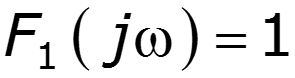
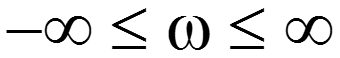
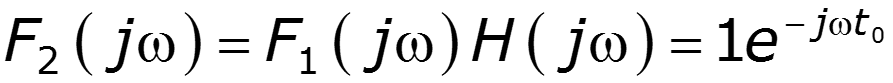
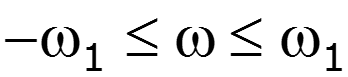
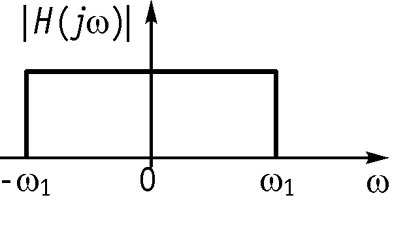
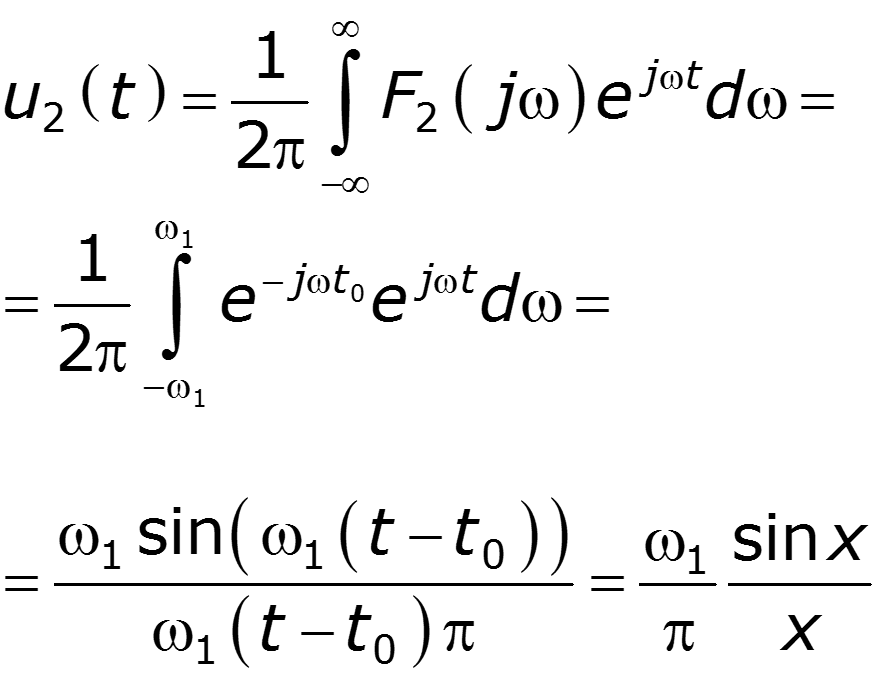
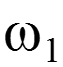
С увеличением ширина главного лепестка сужается, амплитуда увеличивается При с задержкой на время, равное
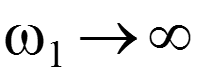
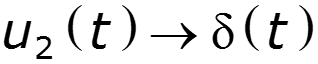
![]()
2.Прохождение единичной функции через идеальный ФНЧ
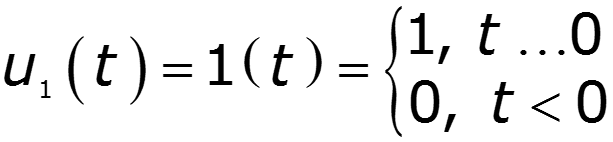
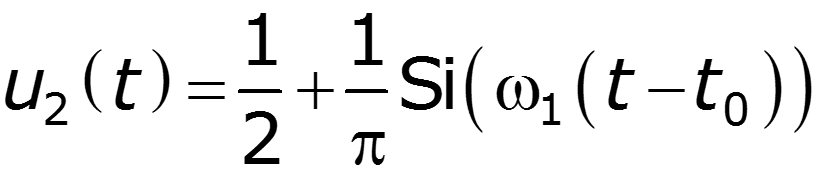
3.Прохождение прямоугольного импульса через идеальный ФНЧ
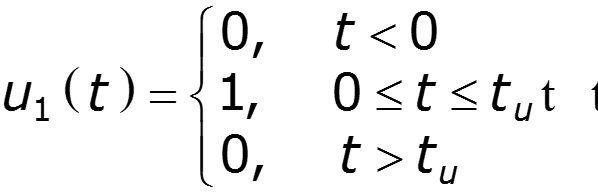
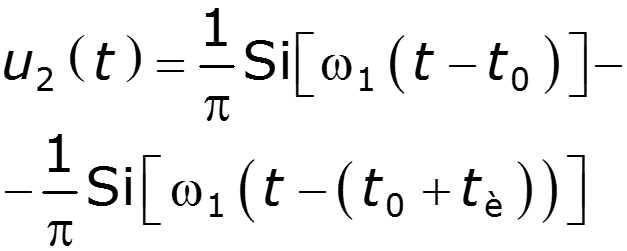
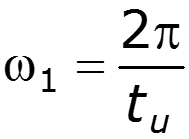
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.