Электрические фильтры. Передаточные функции и частотные характеристики фильтров. Реализация фильтров в виде LC-схем

16.1. Классификация фильтров. 3

16.2. Требования. 9

к  фильтру. 9

16.3. Передаточные функции и частотные характеристики фильтров. 14

16.4. Задача расчёта фильтров. 19

Аппроксимация: 20

Реализация: 21

16.5. Нормирование по частоте. 22

16.6. Фильтры Баттерворта. 26

16.7. Фильтры Чебышева. 47

Полином Чебышева. 49

Поведение полинома  Чебышева. 52

Определение порядка фильтра. 55

Передаточная функция. 57

16.8. Реализация фильтров в виде. 63

LC-схем.. 63

Реализация по методу. 65

Дарлингтона. 65

16.9. Преобразование схем.. 77

LC-фильтров. 77

Преобразование частоты.. 78

Преобразование схемы.. 83

Переход от фильтров НЧ.. 88

к полосовым.. 88

16.10. Реализация фильтров в виде активных RC – схем.. 95

Звено ФНЧ  2-го порядка. 95

Звено ФНЧ 1-го порядка. 101

Реализация ARC – фильтров высокого порядка. 104

Фильтры Золотарева. 107

16.11. Дискретные фильтры.. 109

Порядок расчёта дискретного фильтра. 123

Цифровые фильтры.. 130

16. Электрические фильтры

16.1. Классификация фильтров

 

· По характеру полосы пропускания:

1)  Фильтры нижних частот (ФНЧ)

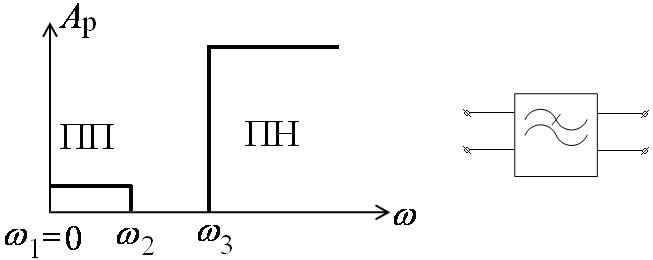
2)  Фильтр верхних частот (ФВЧ)

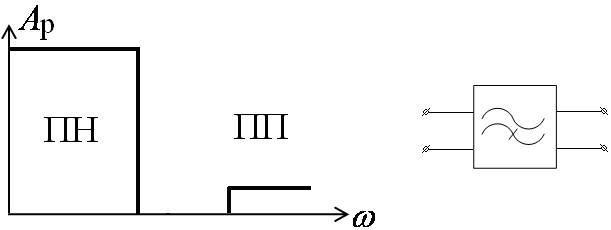
3)  Полосовые фильтры (ПФ)

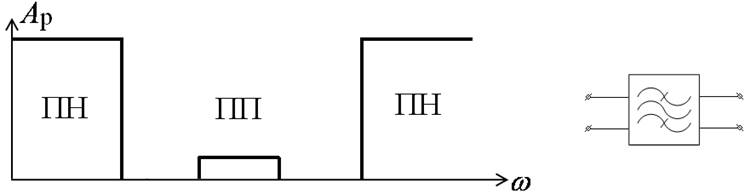
4)  Заграждающие фильтры (ЗФ)

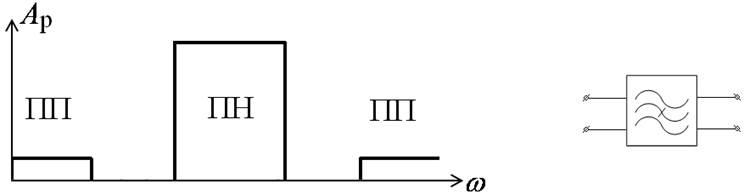
5) Многополосные фильтры

· По наличию источников:

1)  Активные фильтры

2)  Пассивные фильтры

· По элементной базе:

1)  LC - фильтры

2)  RC - фильтры

3)  RLC – фильтры

4)  Кварцевые фильтры

5)  Магнитострикционные фильтры

6)  Электромеханические фильтры

7)  Цифровые фильтры

8)  Акустоэлектронные фильтры

9)  Оптоэлектронные фильтры

10) С переключаемыми конденсаторами

16.2. Требования

к  фильтру

 

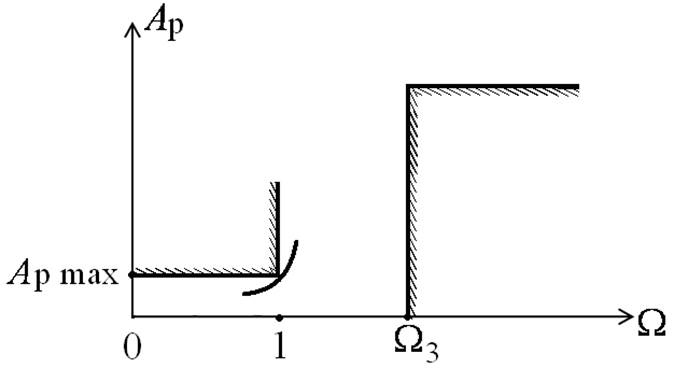
Идеальный фильтр

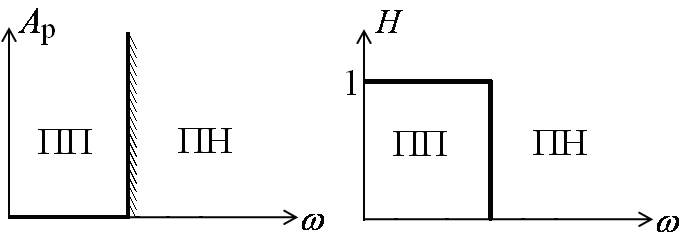
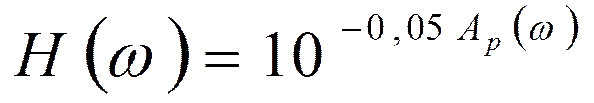
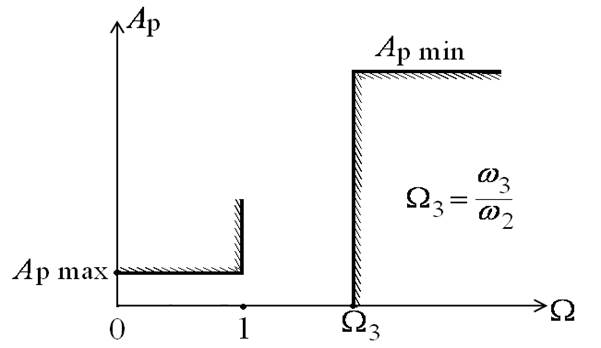
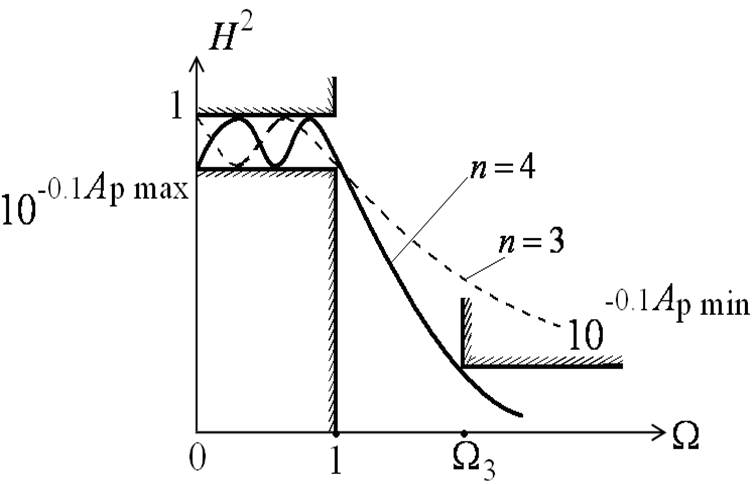
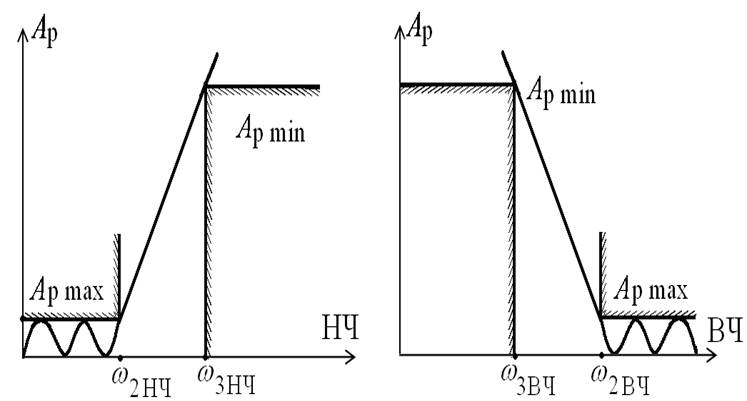
Требования к характеристике рабочего ослабления

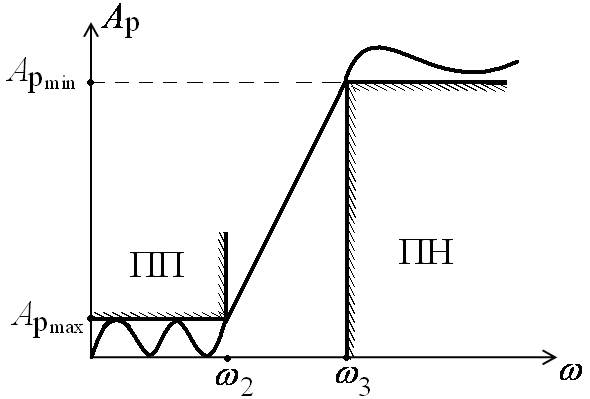
Требования к квадрату АЧХ

16.3. Передаточные функции и частотные характеристики фильтров

 

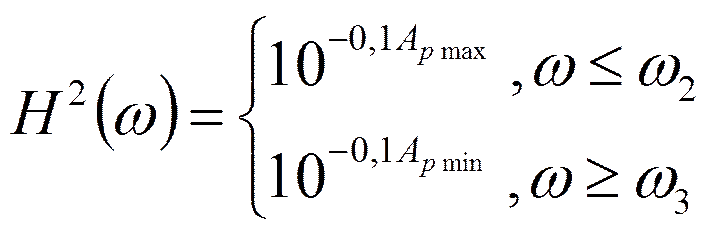
Полиномиальные фильтры

Передаточная функция:

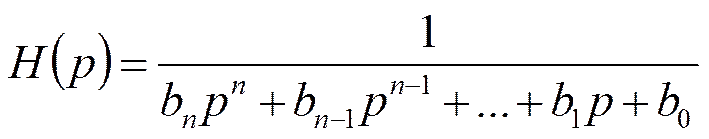
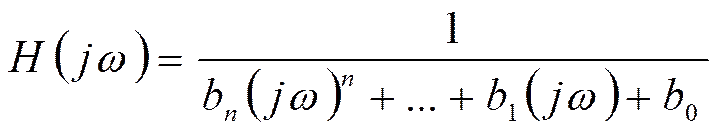
АЧХ:

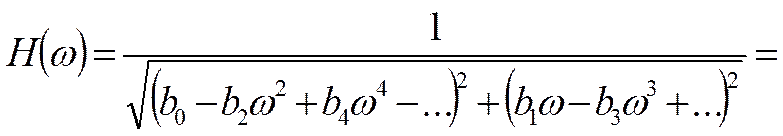
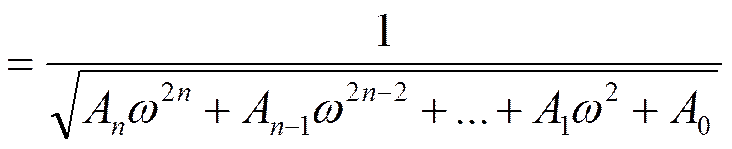
Квадрат АЧХ:

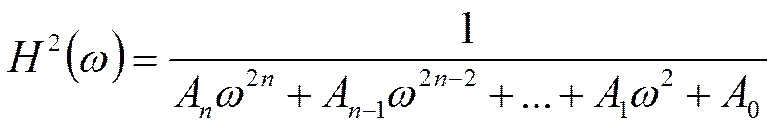
Рабочее ослабление:

16.4. Задача расчёта фильтров

 

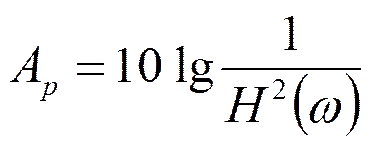
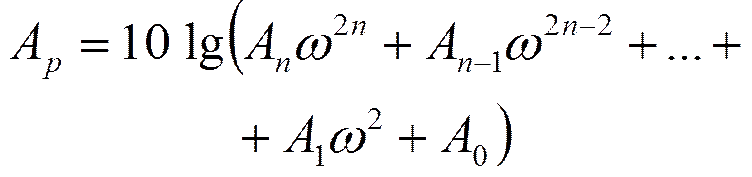
1 этап. Аппроксимация

2 этап. Реализация

Аппроксимация:

В выражении 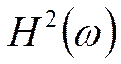 отыскивают такие коэффициенты 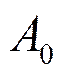, ,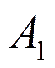…,,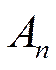 при которых квадрат АЧХ 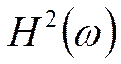 удовлетворяет заданным требованиям.

Реализация:

1)  в виде LC – схемы;

2)  в виде RC – схемы;

3)  в виде цифрового фильтра;

и т.д.

16.5. Нормирование по частоте

 

Нормированная частота:

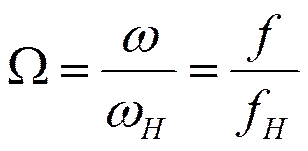
Обычно:

Тогда:

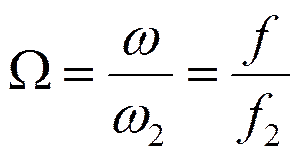
Нормированная граничная частота полосы пропускания

Квадрат АЧХ:

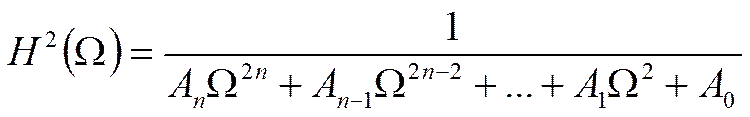
Чтобы найти реальную частоту, нужно:

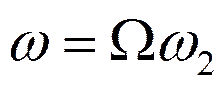
или

16.6. Фильтры Баттерворта

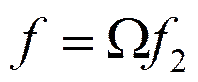
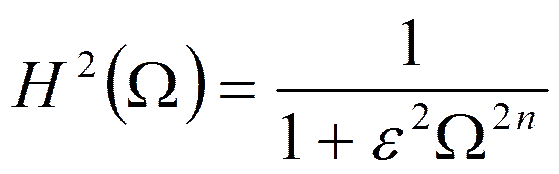
У фильтров Баттерворта

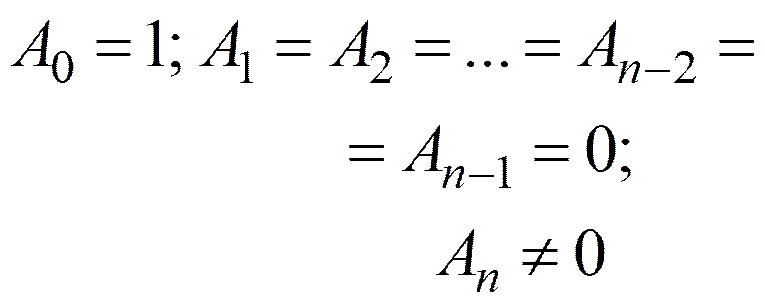
Квадрат АЧХ:

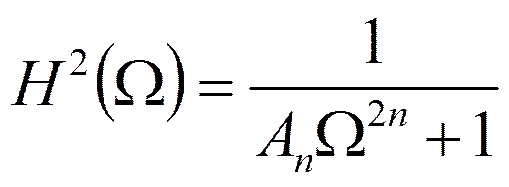
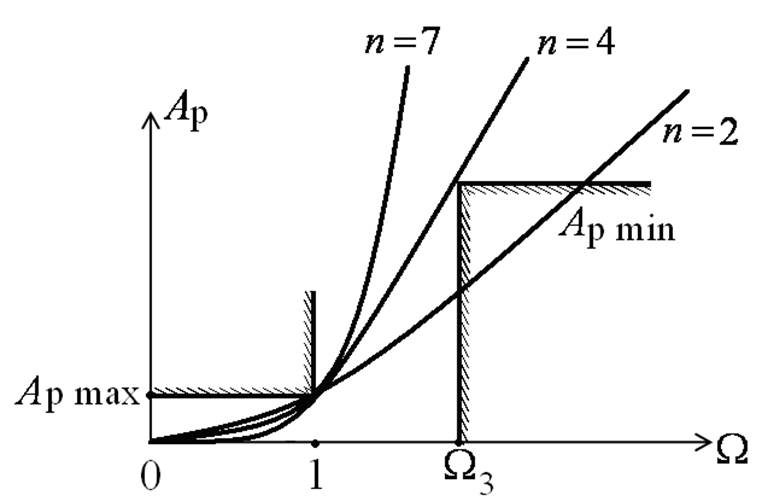
Рабочее ослабление:

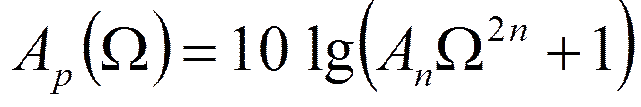
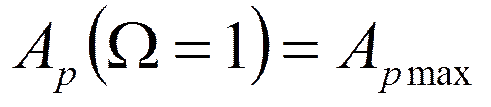
Коэффициент А_n найдём из условия:

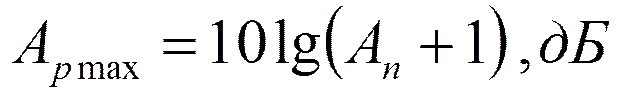
Откуда:

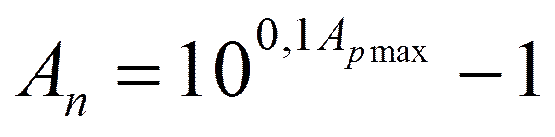
Величину

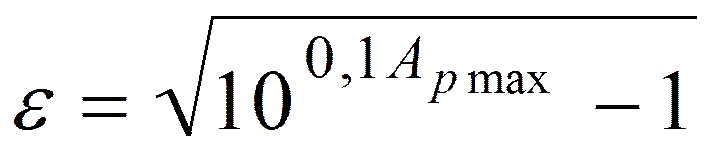
называют коэффициентом неравномерности ослабления в полосе пропускания.

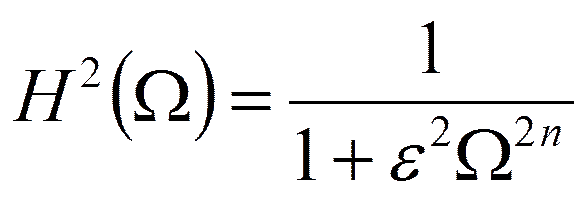
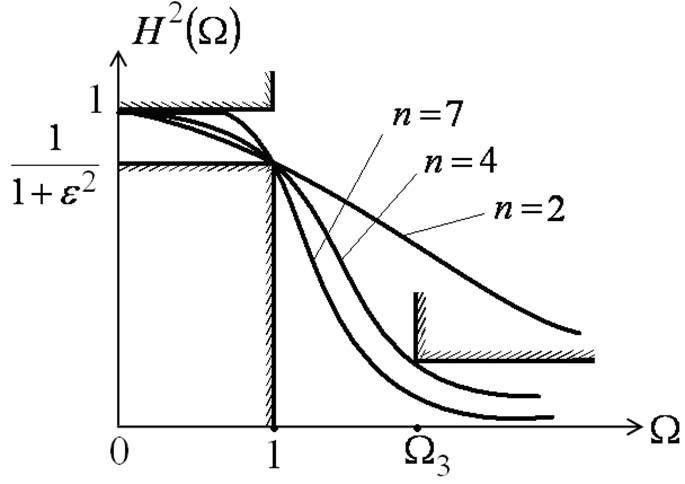
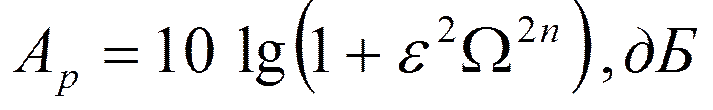
Порядок фильтраnвыбирается так, чтобы

или

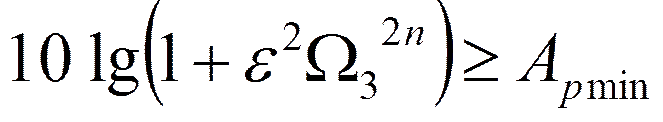
Откуда

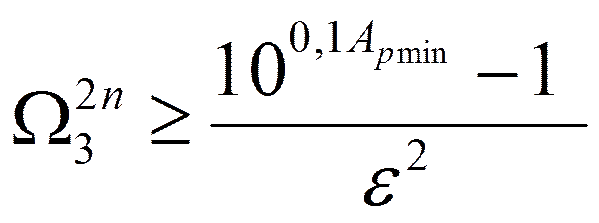
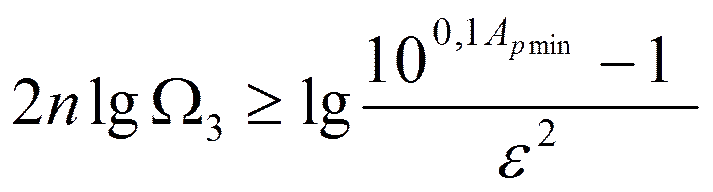
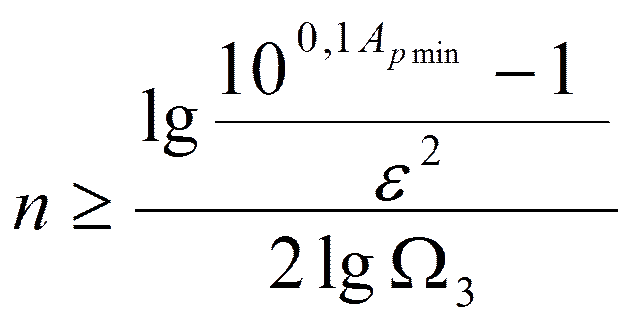
Передаточная функция фильтра Баттерворта

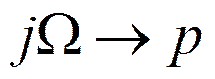
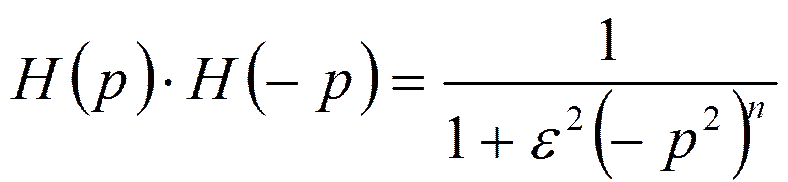
Нечётное n:

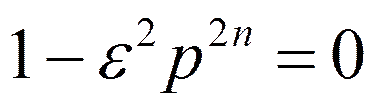
Чётное n:

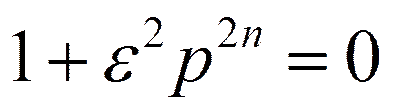
Найдём полюсы для чётного n:

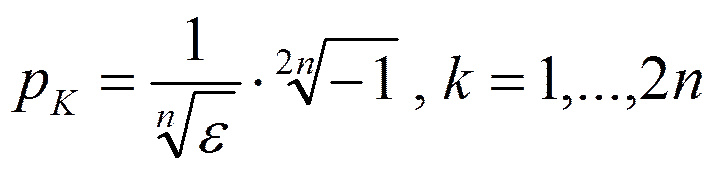
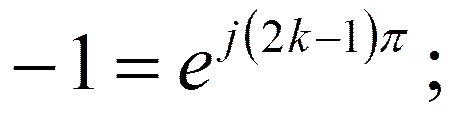
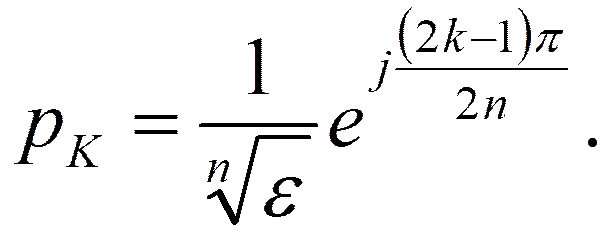
Для нечётногоn:

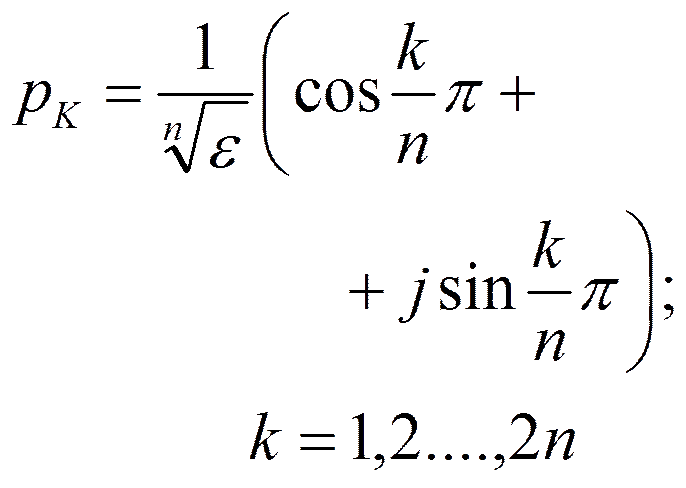
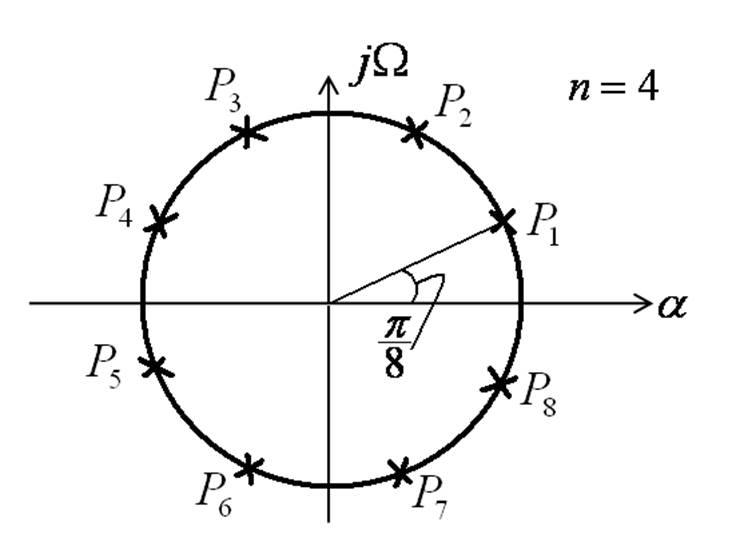
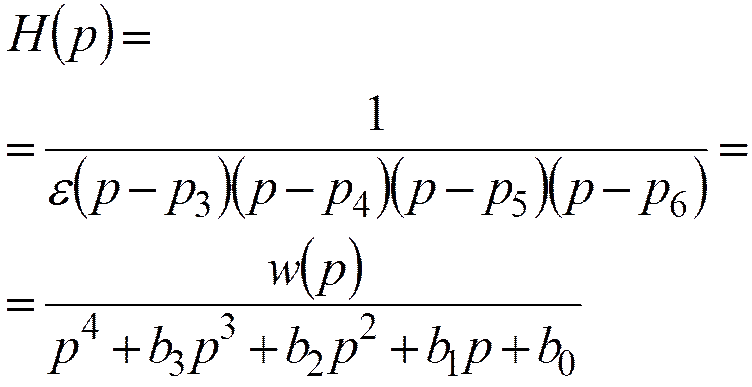
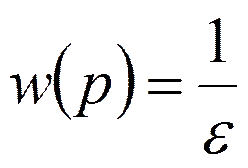
 - полином Баттерворта

Поэтому фильтры

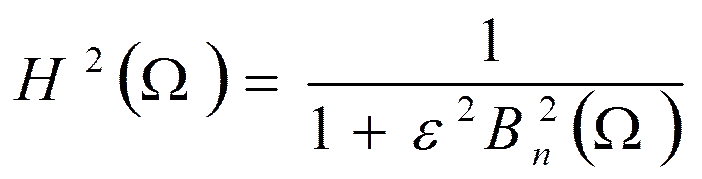
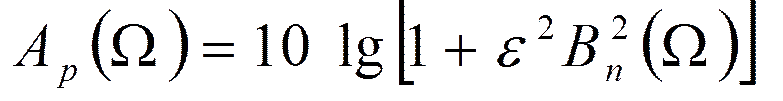называют фильтрами Баттерворта.

16.7. Фильтры Чебышева

 

Если в выражениях для квадрата АЧХ и рабочего ослабления вместо полинома Баттерворта подставить полином Чебышева, то получим фильтры Чебышева.

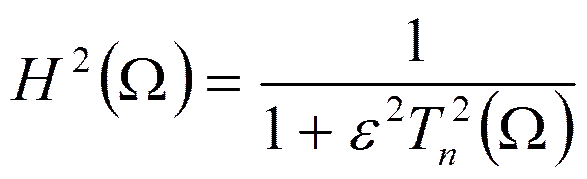
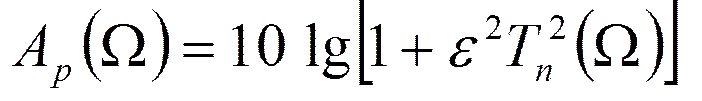
Полином Чебышева

………………………………………..

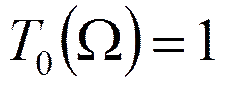
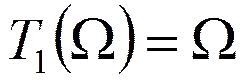
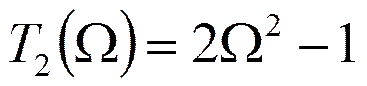
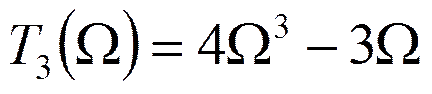
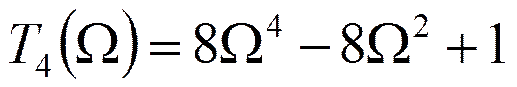
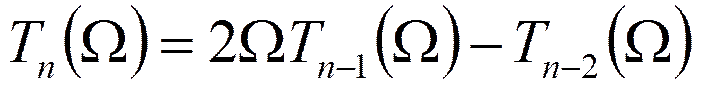
Другая форма записи полинома Чебышева:

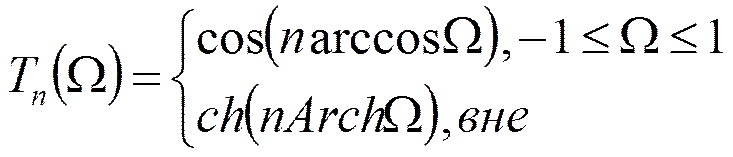
Коэффициент при старшем члене полинома Чебышева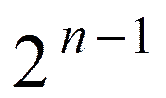

Поведение полинома Чебышева

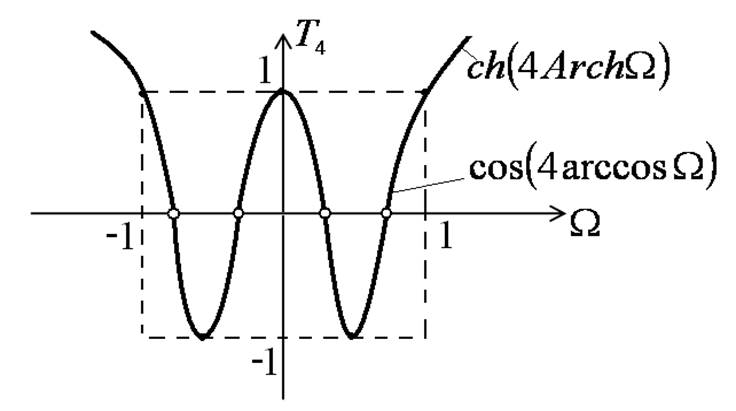
В интервале 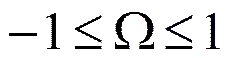 полином Чебышева -го порядка принимает 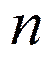 раз нулевые значения и 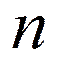+1 раз крайние значения, равные ±1.

Это явление называется Чебышевским альтернансом.

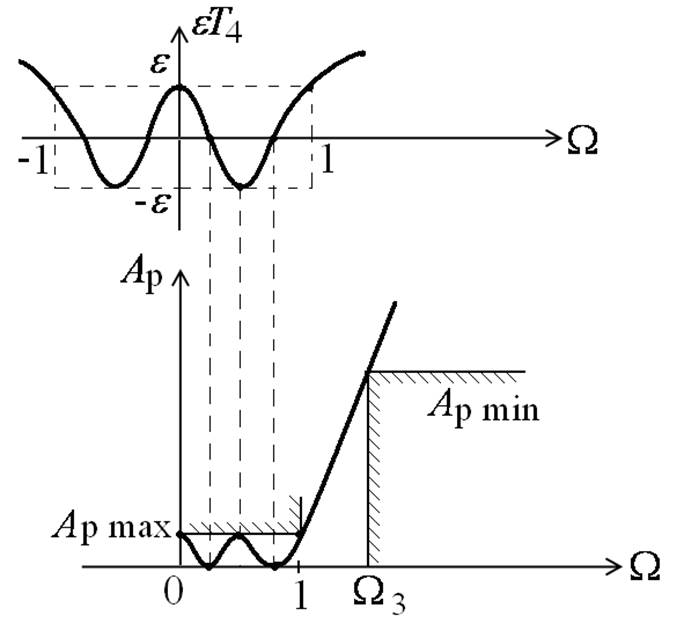
Определение порядка фильтра

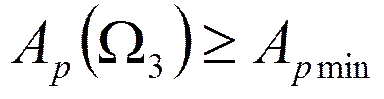
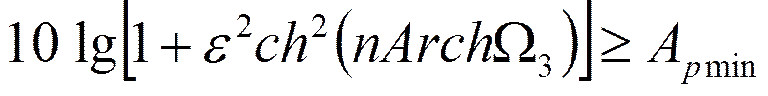Откуда:

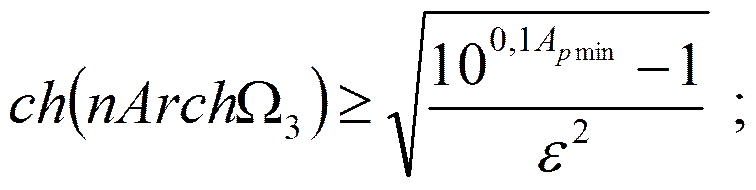
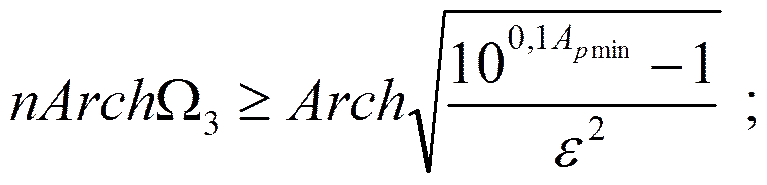
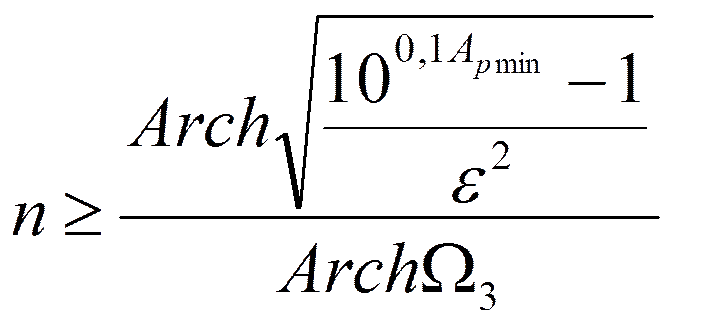
Передаточная функция

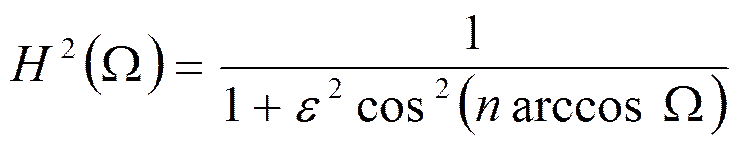
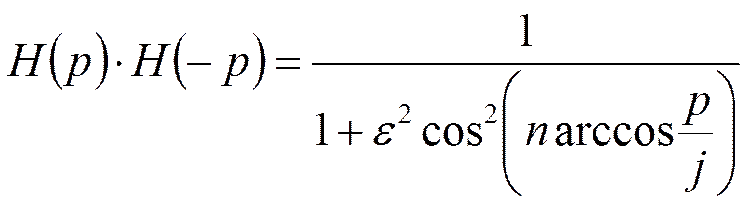
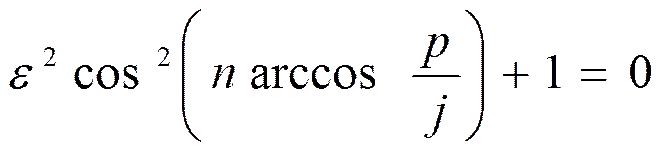
Коэффициент при старшей степени

.

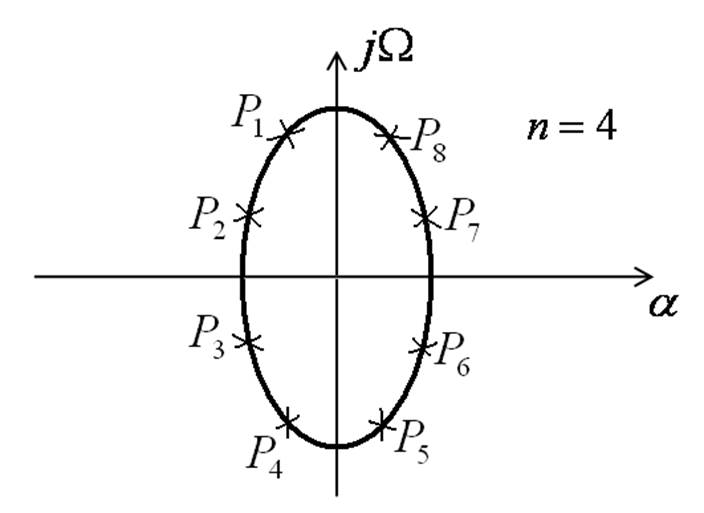
Корни уравнения

16.8. Реализация фильтров в виде

LC-схем

 

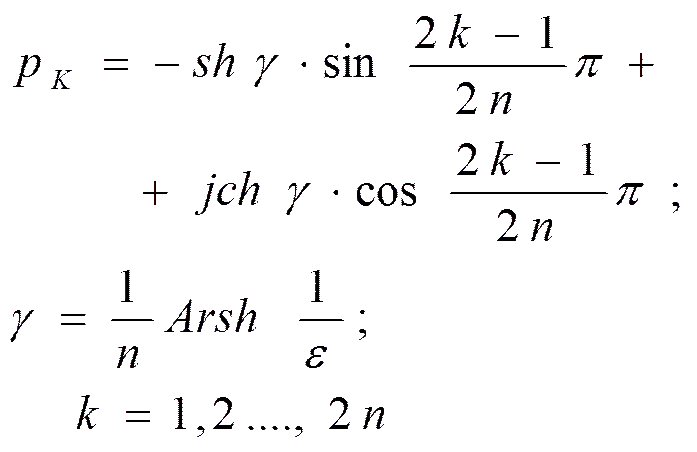
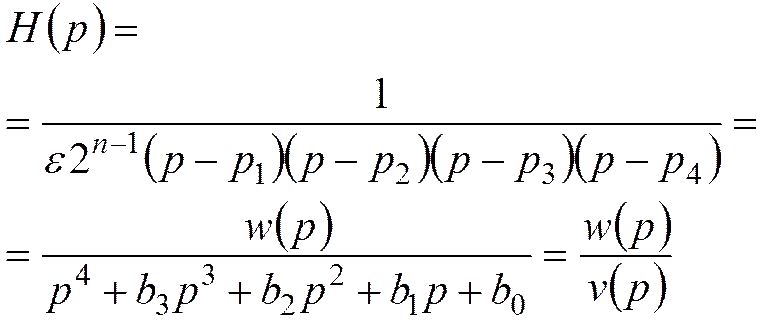
Полиномиальный фильтр

5-го порядка

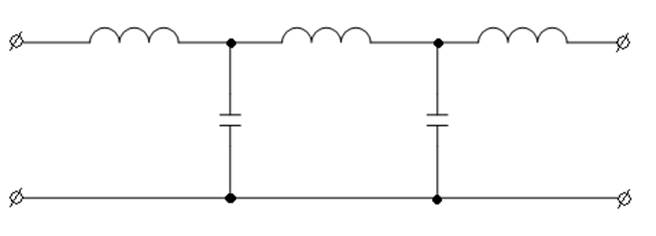
Реализация по методу

Дарлингтона

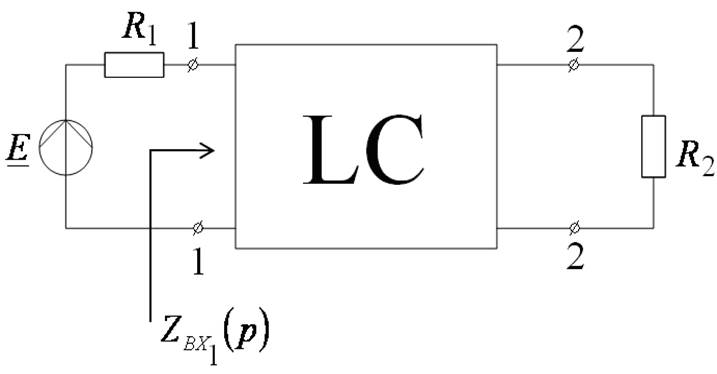
Коэффициент отражения

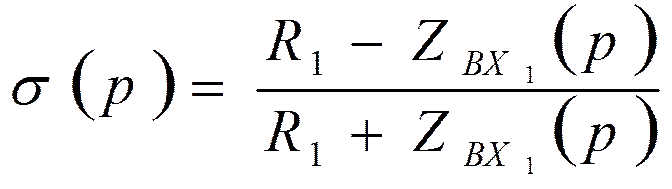
Откуда

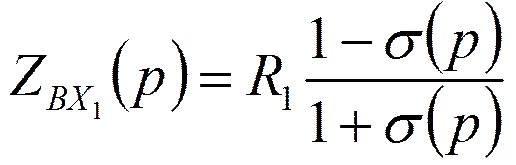
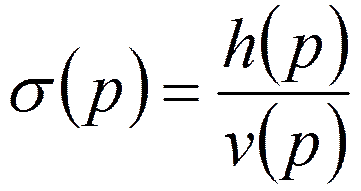
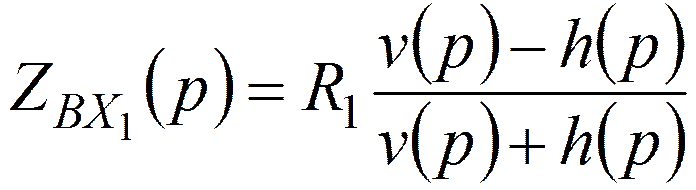
Зная , находят 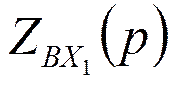 и по этому сопротивлению реализуют двухполюсник методом Кауэра.

Существует связь:

Пример

В результате аппроксимации получено выражение квадрата АЧХ:

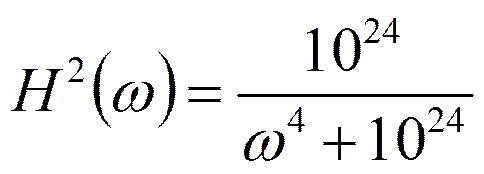
Находим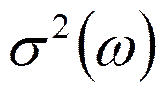

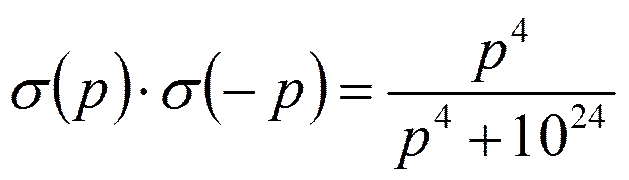
Корни числителя:

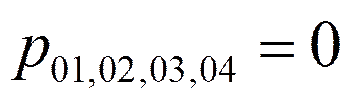
Корни знаменателя:

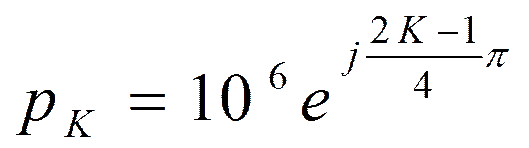
или

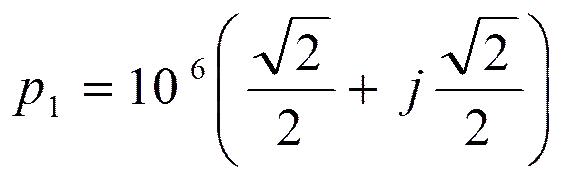
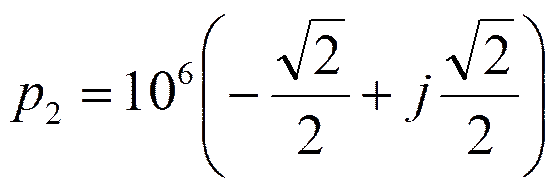
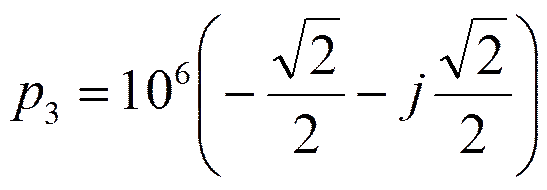
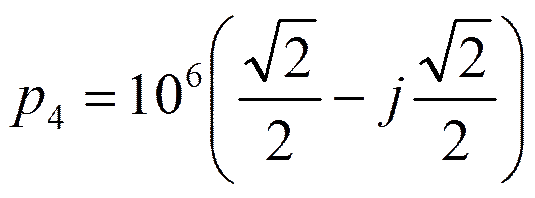
Составим полиномы h(p) и v(p).

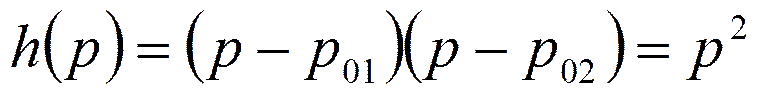
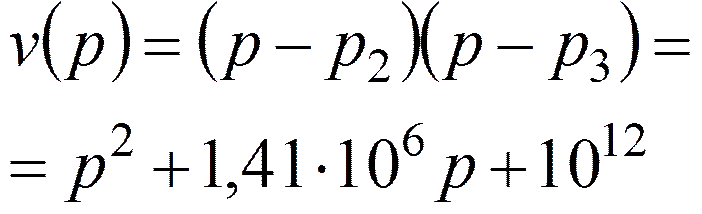
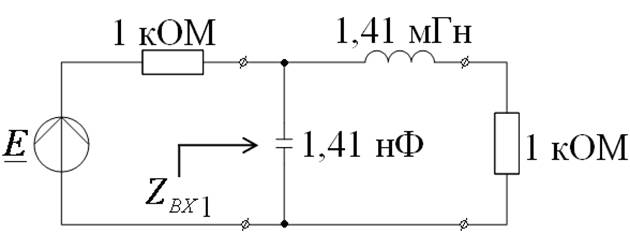
Пусть R₁= 1 кОм

Тогда:

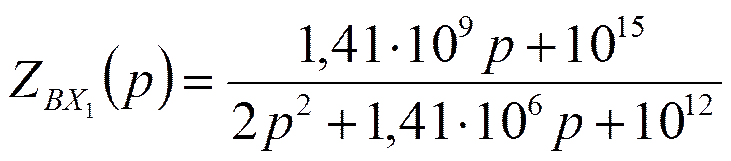
Осуществим реализацию по

1-ой форме Кауэра.

16.9. Преобразование схем

LC-фильтров

 

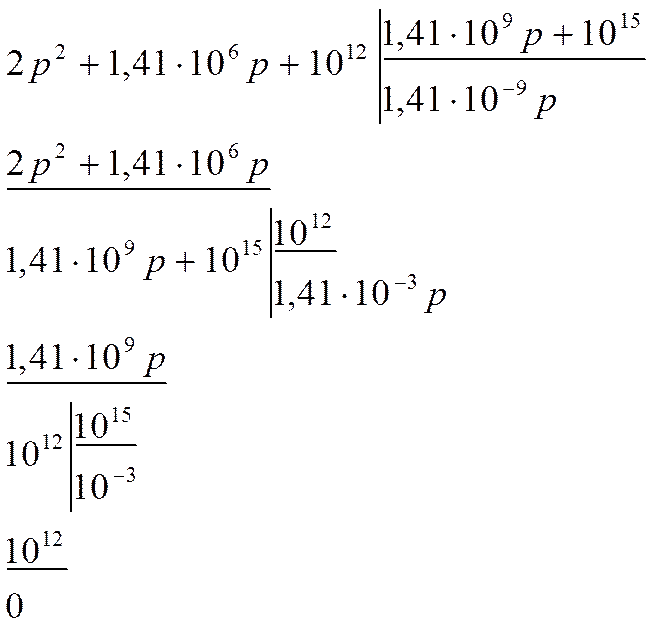
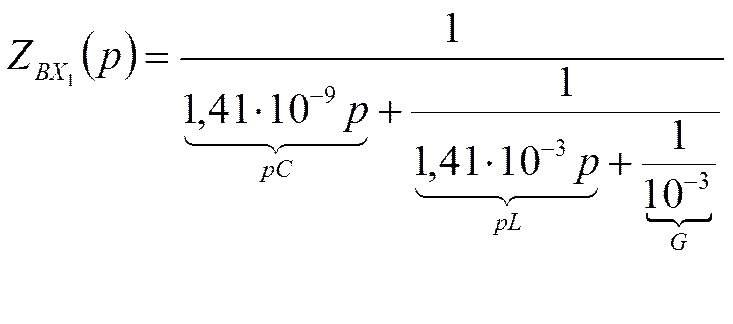
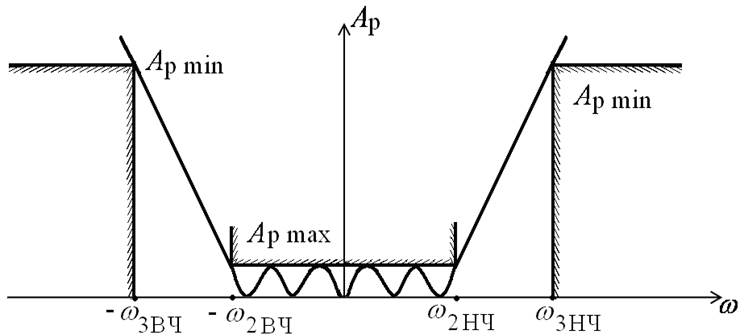
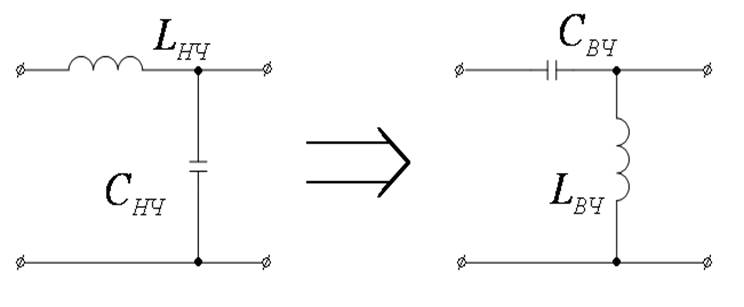
От схем ФНЧ – к схемам ФВЧ, ПФ, ЗФ.

Преобразование частоты

От ФНЧ – к ФВЧ

         

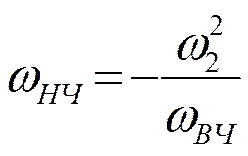
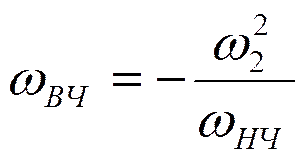
Пример

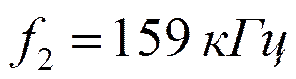
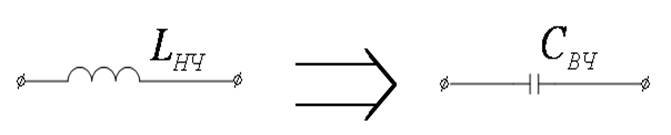
Преобразование схемы

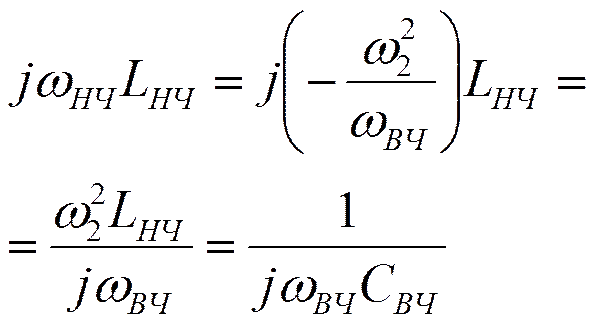
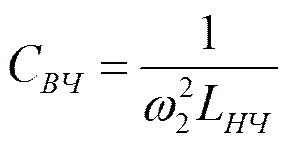
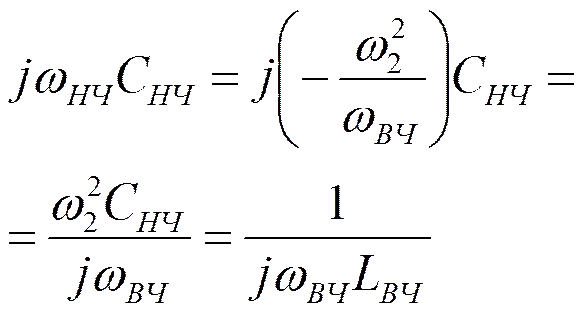
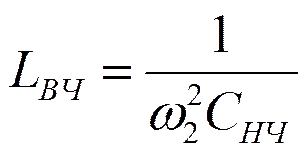
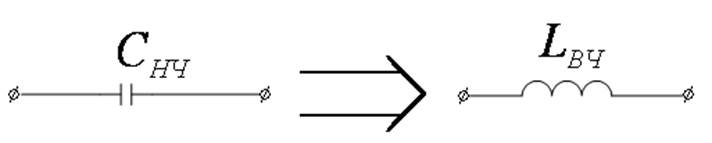
Пример

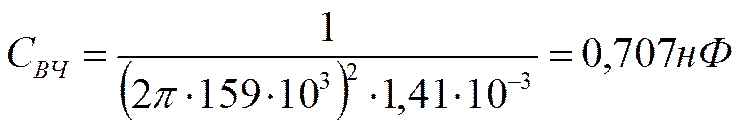
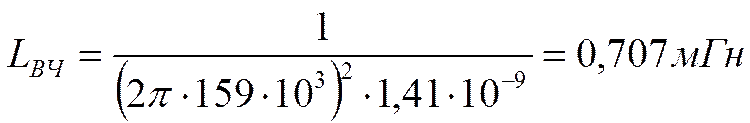
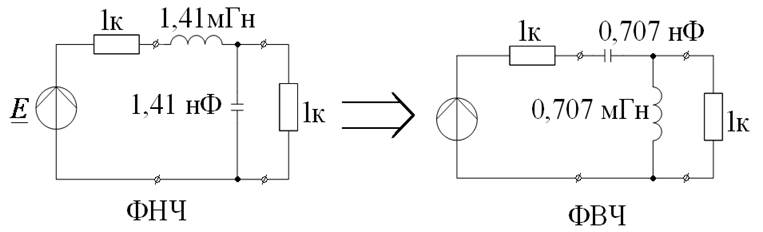
Переход от фильтров НЧ

к полосовым

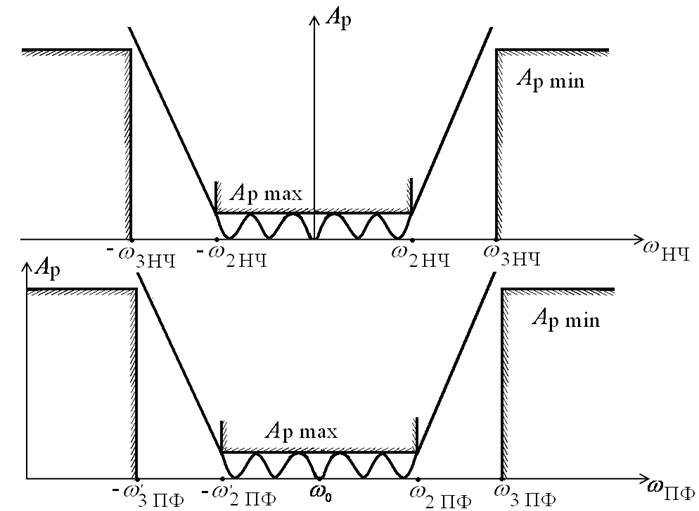
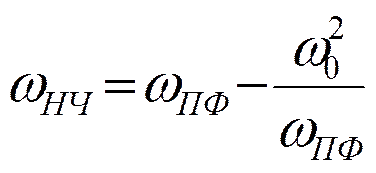
Пример

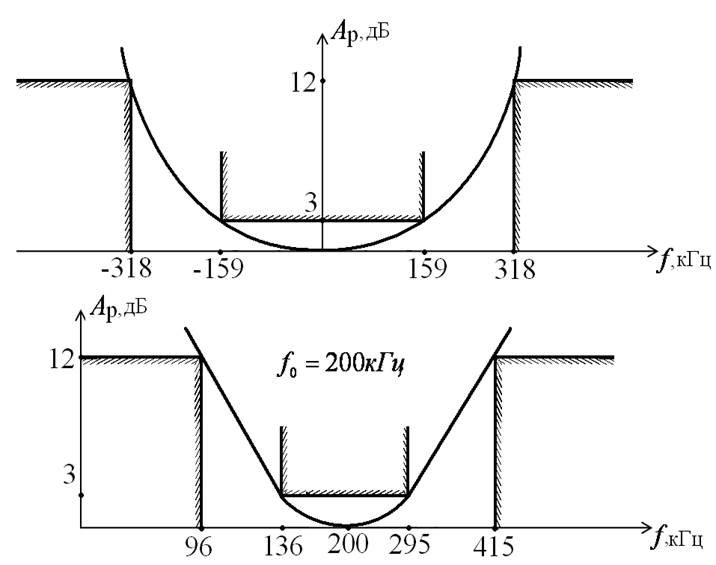
Преобразование схемы ФНЧ в схему ПФ

16.10. Реализация фильтров в виде активных RC – схем

 

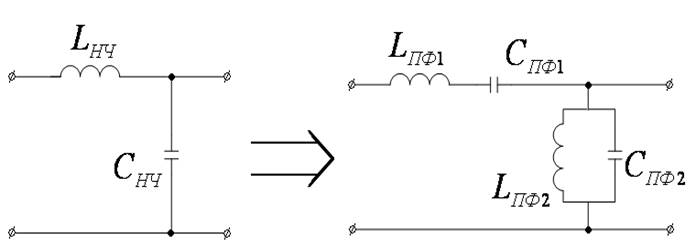
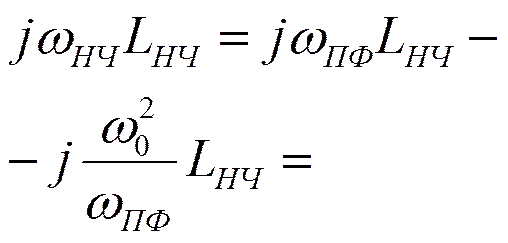
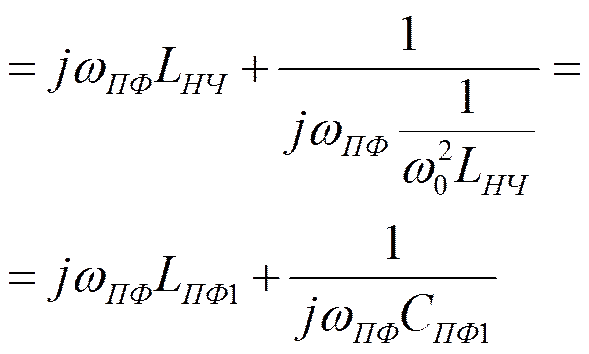
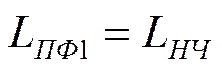
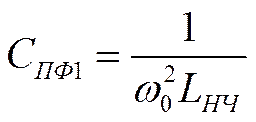
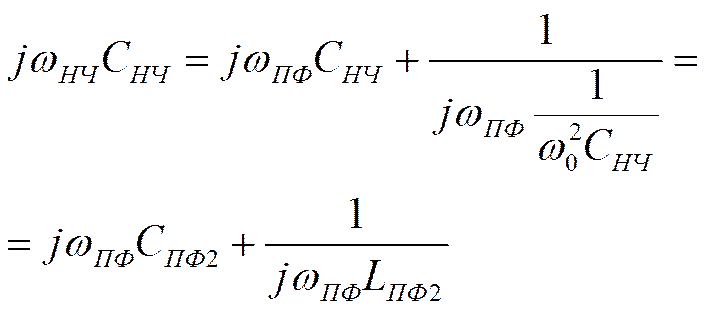
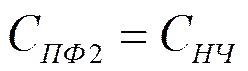
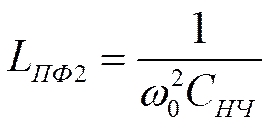
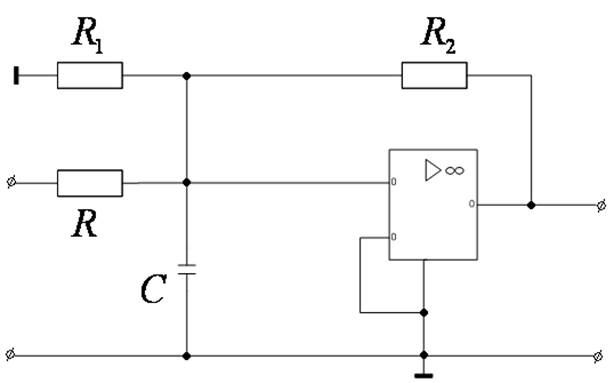
Звено ФНЧ  2-го порядка

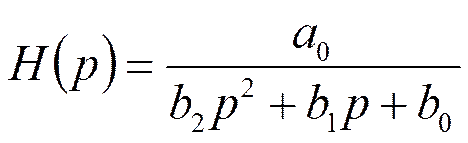
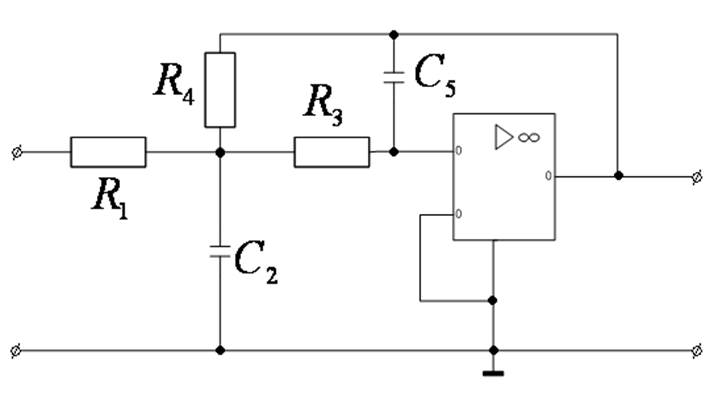
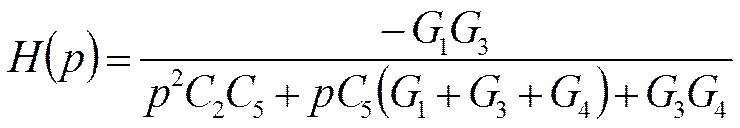
или

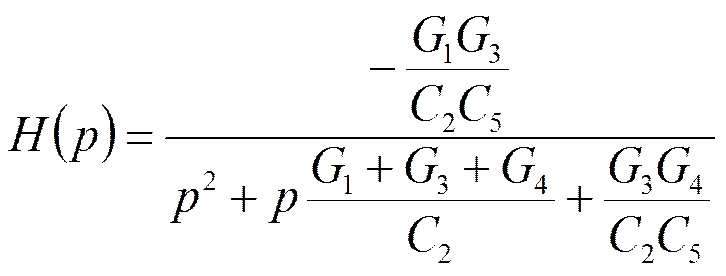
Пример. Реализовать ФНЧ Баттерворта 2-го порядка в виде ARC – схемы.

;      

    

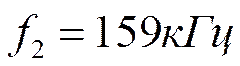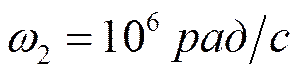
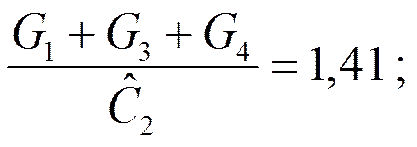
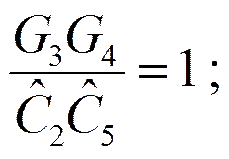
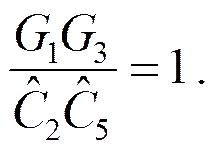
Выберем                 

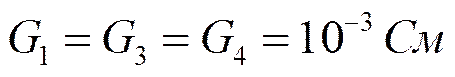
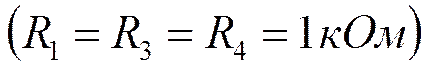
Тогда

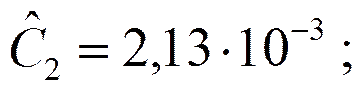
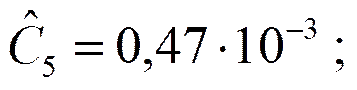
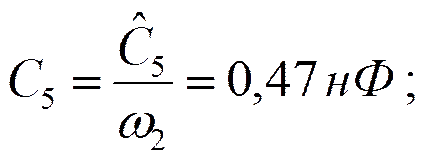
Звено ФНЧ 1-го порядка

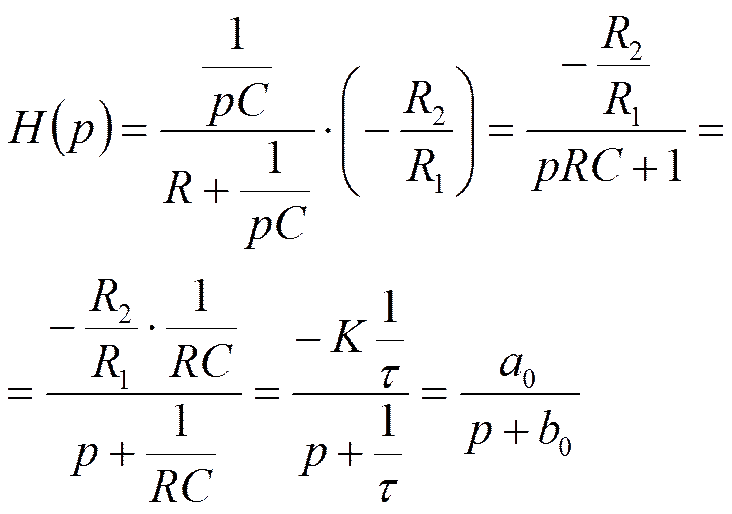
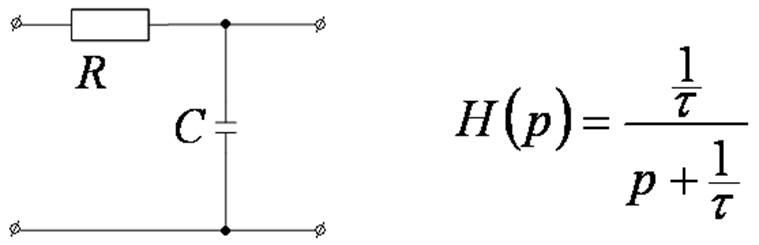
Реализация ARC – фильтров высокого порядка

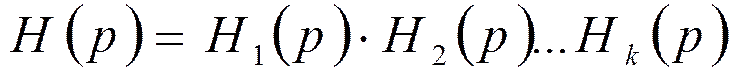
Передаточную функцию разбивают на произведение передаточных функций первого и второго порядка.

Пример

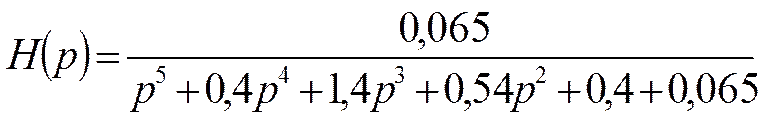
Найдём полюсы :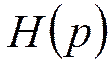

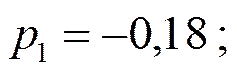
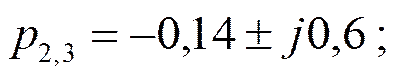
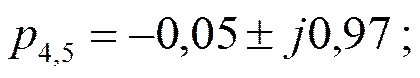
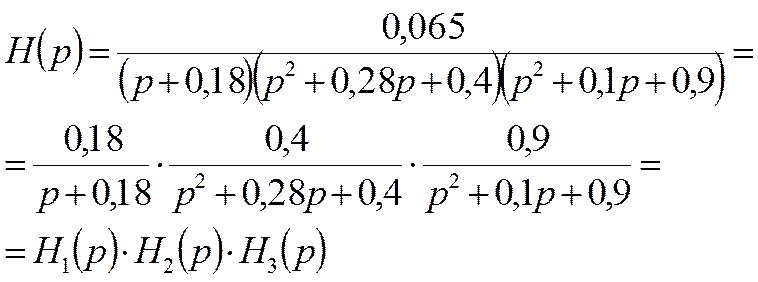
Звено 1-го порядка и два звена 2-го порядка включаются каскадно.

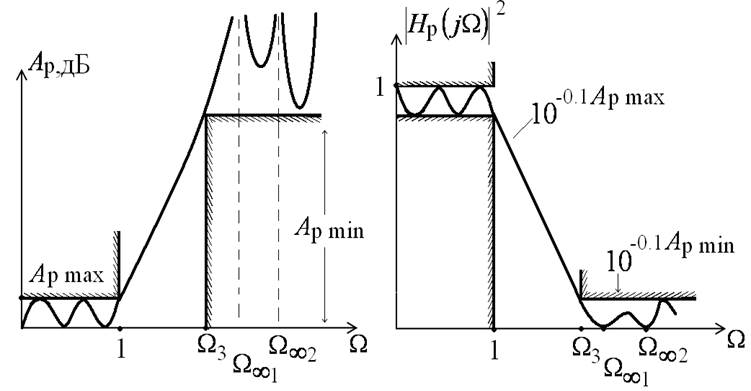
Фильтры Золотарева

Это фильтры со всплесками ослабления в полосе непропускания или фильтры с нулями передаточной функции.

16.11. Дискретные фильтры

 

Один из методов расчёта – это переход от  аналогового фильтра к  цифрового фильтра.

Стандартное преобразование 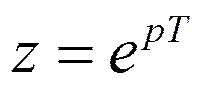, откуда

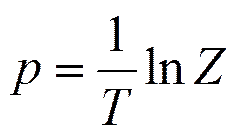
Такая подстановка в  не приведёт к дробно-рациональной функции .

Разложим стандартное преобразование в ряд Тейлора:

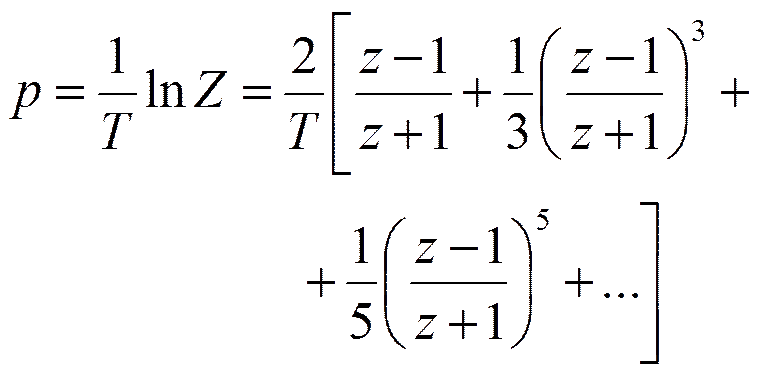
Оставляя первый (линейный) член, имеем:

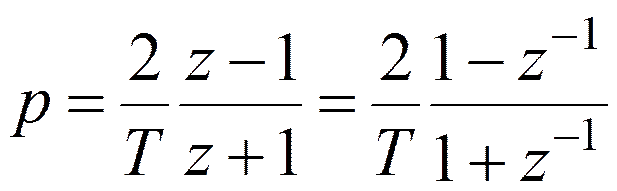
В общем виде:

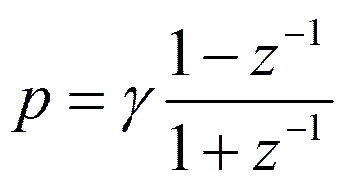
Это преобразование называется билинейным. Здесь 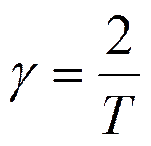. Часто используют другие выражения для коэффициента пропорциональности .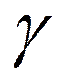

Фильтры

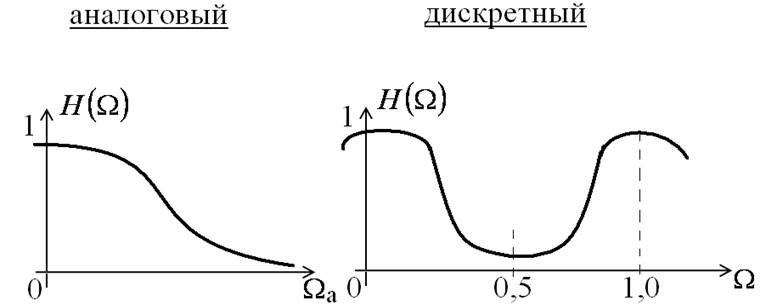
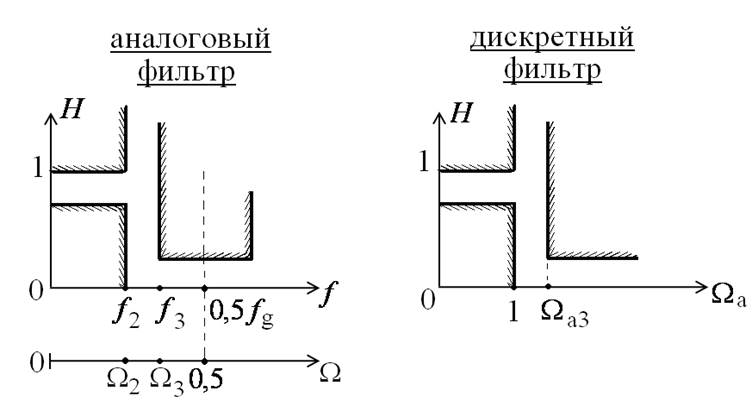
АЧХ дискретного фильтра периодически повторяется с периодом 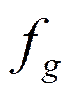. Заметим, что когда ,

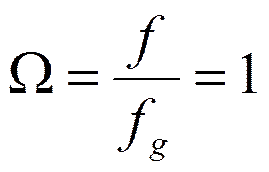
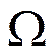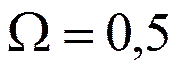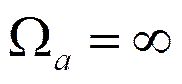Использовать можно диапазон  от 0 до 0,5. Т.е. частота  для дискретного фильтра соответствует частоте   аналогового фильтра.

Установим соответствие шкал частот этих фильтров. Для этого перепишем билинейное преобразование в виде:

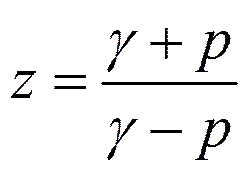
И подставим 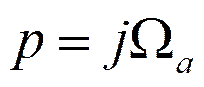 и .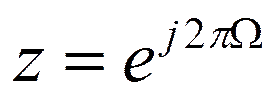

Тогда

Откуда:

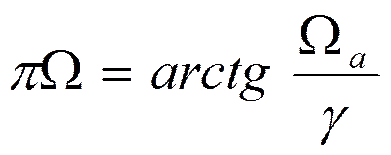
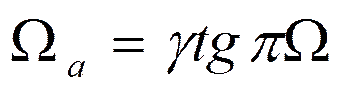
При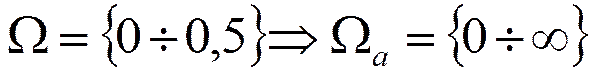 

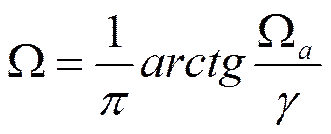
При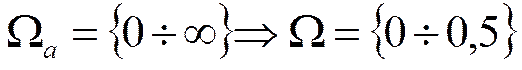

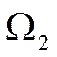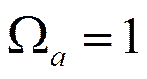Необходимо, чтобы частота  дискретного фильтра соответствовала частоте  аналогового фильтра:

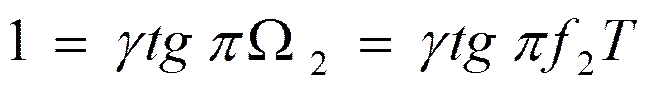
Откуда

При 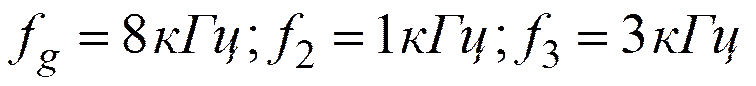 получаем

Порядок расчёта дискретного фильтра

1. Пересчитать требования к ДФ в требованиях к АФ.

2. Найти из справочника по требованиям к АФ передаточную функцию Н(р) аналогового фильтра.

(Или рассчитать Н(р) любым другим способом).

3. С помощью билинейного преобразования перейти от Н(р) к Н(z).

4. Реализовать Н(z) в виде любой (или требуемой) схемы.

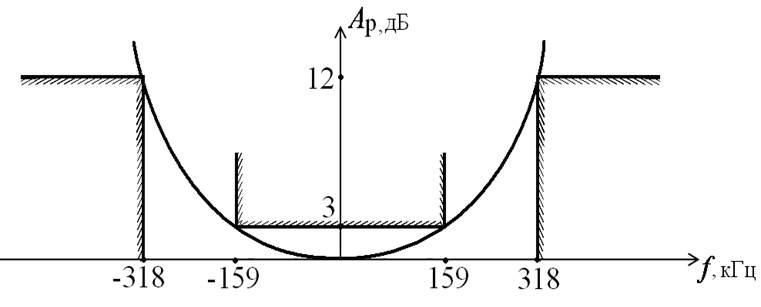
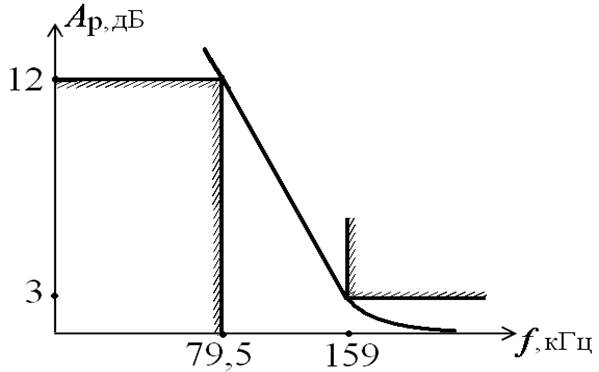
Пример

Требования к ДФ:

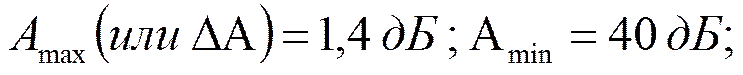
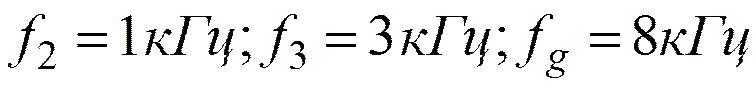
1.  Определяем :

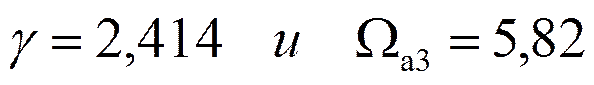
2. Находим Н(р) АФ:

При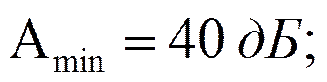

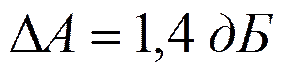
и 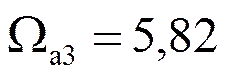 по справочнику Христиан Э.,Эйзенман Е. «Таблицы и графики по расчёту фильтров» (М.: Связь, 1975) находим

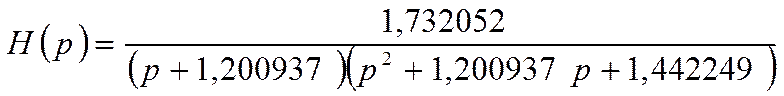
3. Переходим к :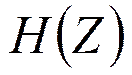

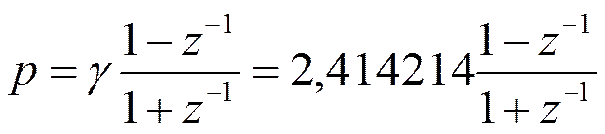
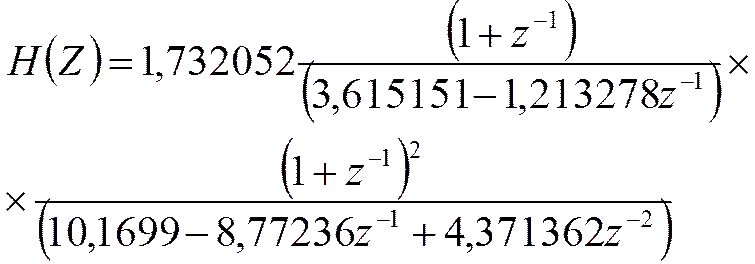
Приведём Н(z) к стандартному виду:

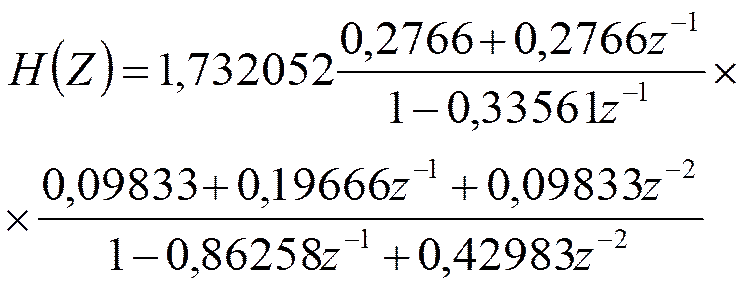
4. Строим схему фильтра.

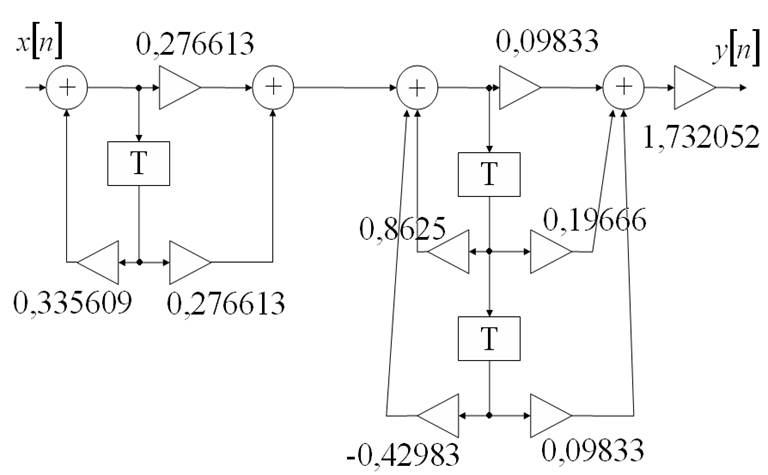
Цифровые фильтры

1. Числа представляются двоичным кодом.

2. Ячейки памяти имеют конечную разрядность, т.е. числа представляются с ошибкой. Возникает шум квантования. Умножение также выполняется с округлением результата.

3. Расчёт ЦФ включает расчёт разрядностей АЦП, ЦАП, регистров оперативной памяти.