
5.2. Резонанс токов в параллельном колебательном контуре
 |
Идеальный контур
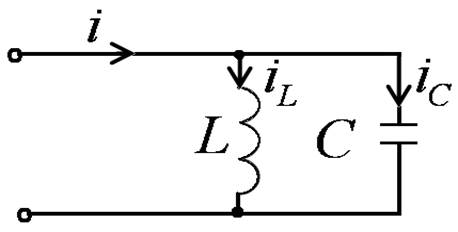
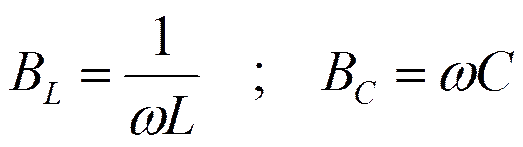
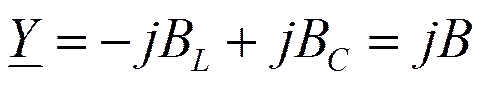
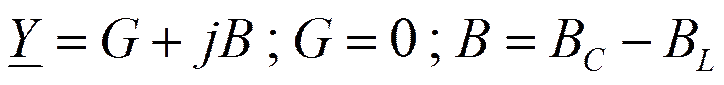
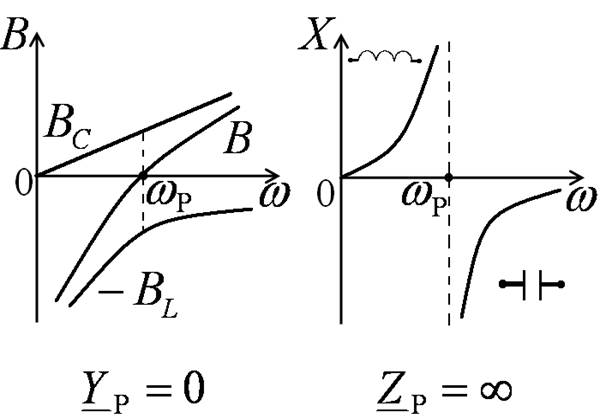
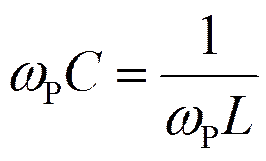 - условие резонанса
- условие резонанса

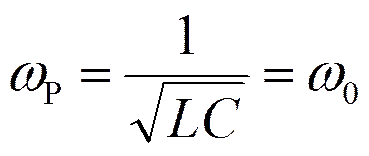
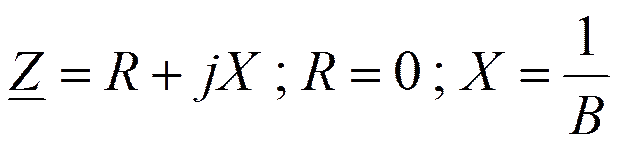
При ω=ωр
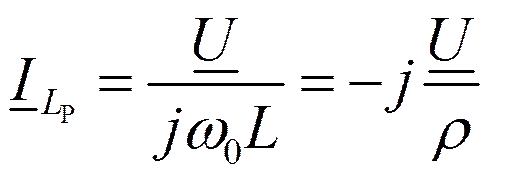
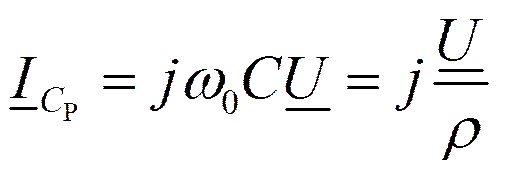
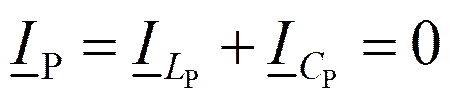
Здесь, как и ранее ,
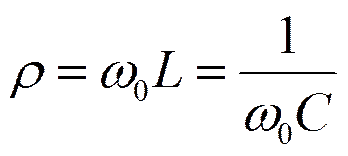
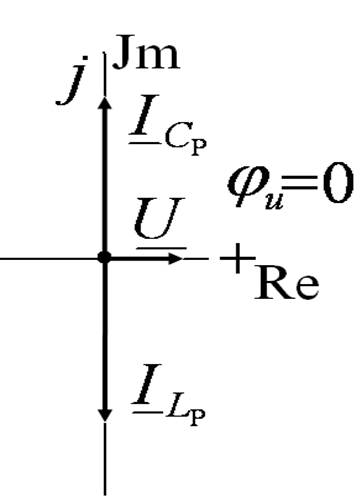
Резонансная частота в реальном контуре
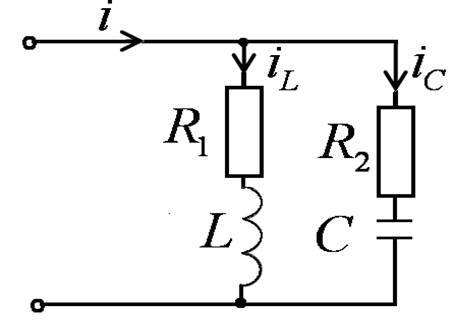
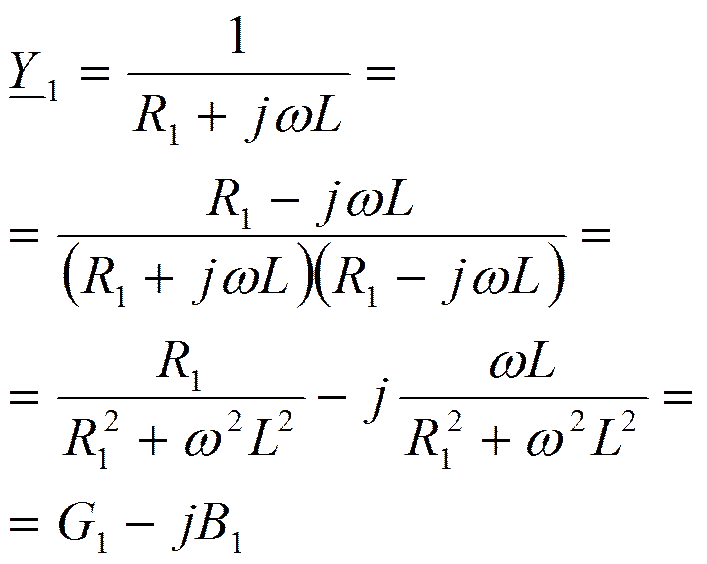
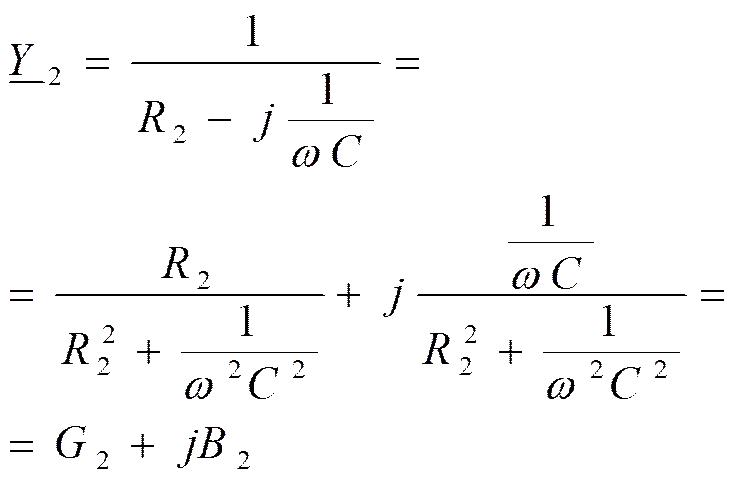
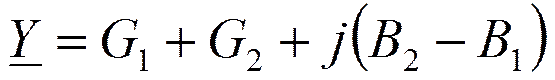
Найдётся частота, на которой реактивные проводимости ветвей компенсируются. Это резонансная частота контура.
В2=В1 или
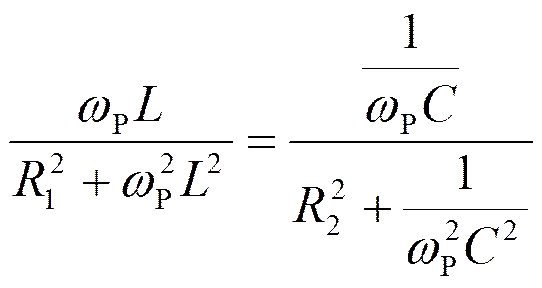
Отсюда

|
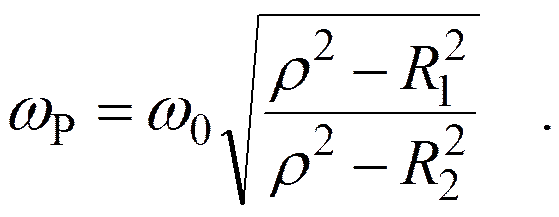
В двух случаях:
а)
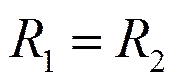 и б)
и б)
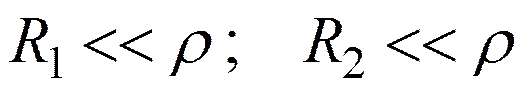
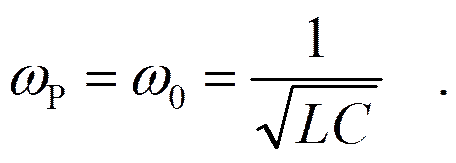
Параллельный контур с малыми потерями

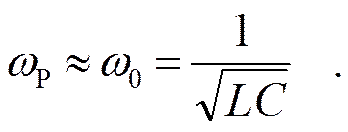
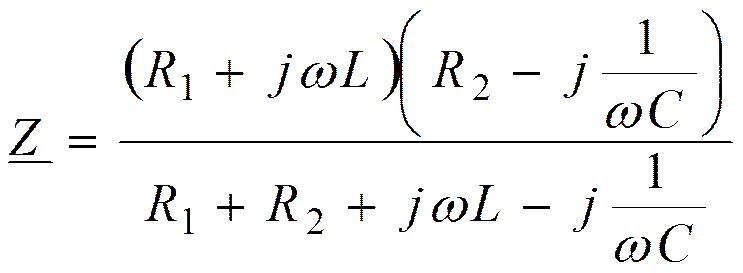
На частоте резонанса
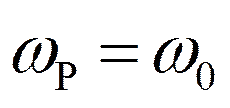
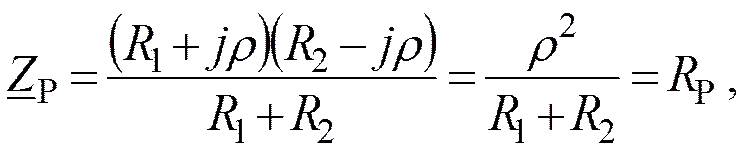 т.е. является активным.
т.е. является активным.

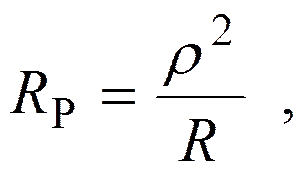
где R = R1 + R2 .
Обозначим, как и ранее,
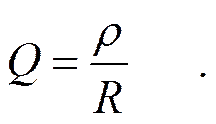
Тогда

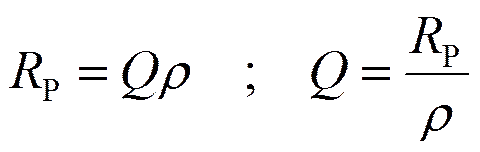
![]()
Чем меньше потери, тем выше добротность контура.
![]() Чем меньше потери, тем
больше сопротивление контура на резонансной частоте.
Чем меньше потери, тем
больше сопротивление контура на резонансной частоте.
Токи в ветвях при резонансе:
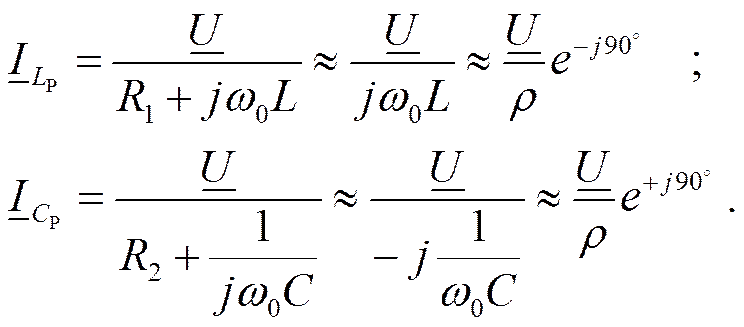
Ток в общей ветви:
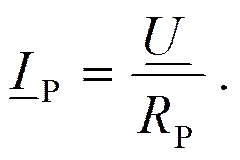
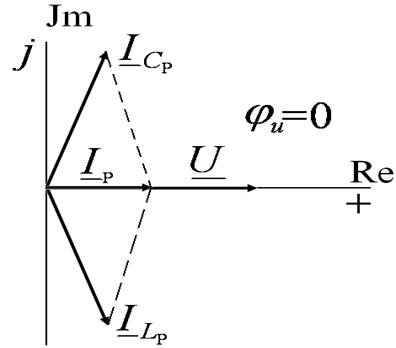


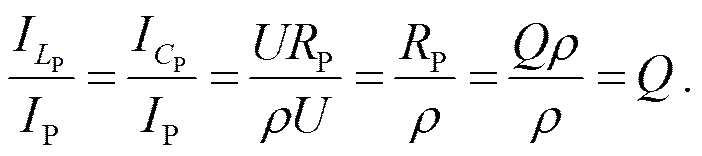
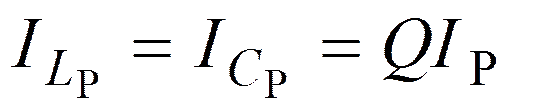
Токи в ветвях в Q раз
![]() превышают общий ток.
Поэтому резонанс называют резонансом токов.
превышают общий ток.
Поэтому резонанс называют резонансом токов.
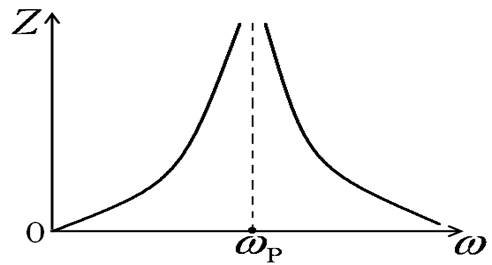
Частотная характеристика параллельного контура с малыми потерями
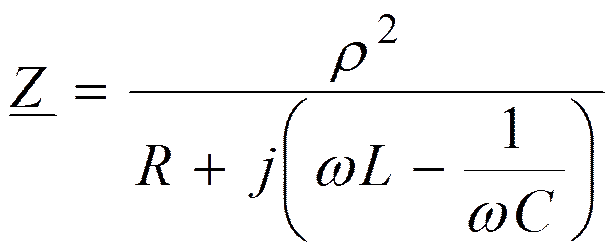
Заметим, что
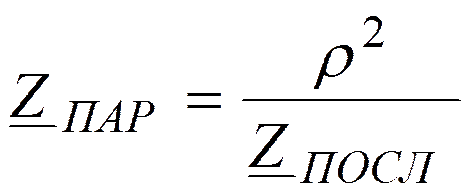
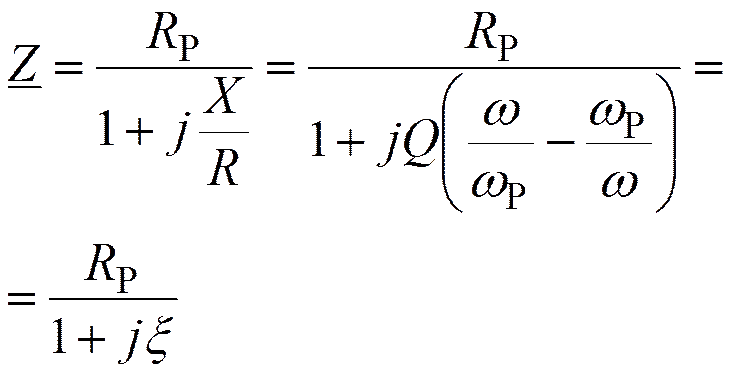
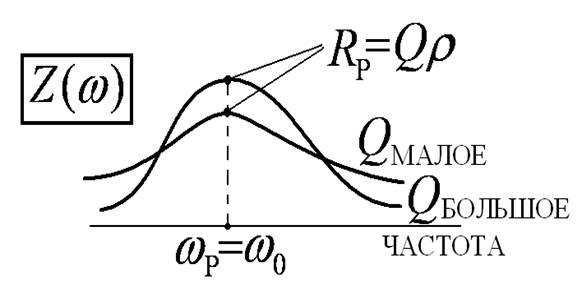
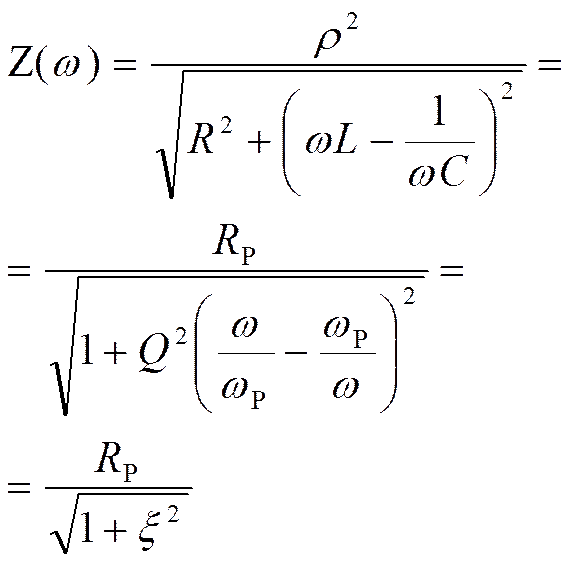
Если поддерживать U(w) постоянным на всех частотах, то изменяться будет ток обратно пропорционально Z(w).
Если поддерживать постоянный ток I(w), то изменяться будет напряжениепрямо пропорционально Z(w):
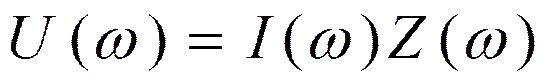
Нормированная частотная характеристика напряжения
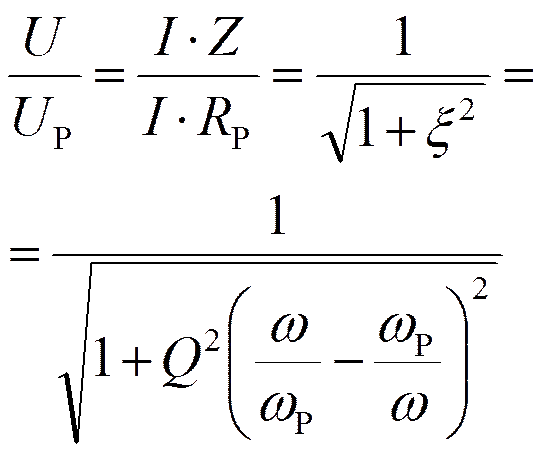
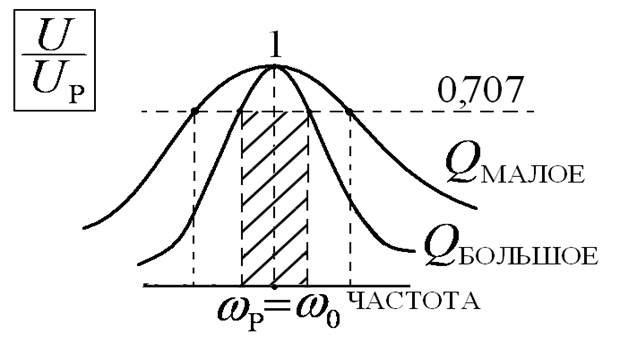
Влияние на добротность Q сопротивления нагрузки и внутреннего сопротивления генератора
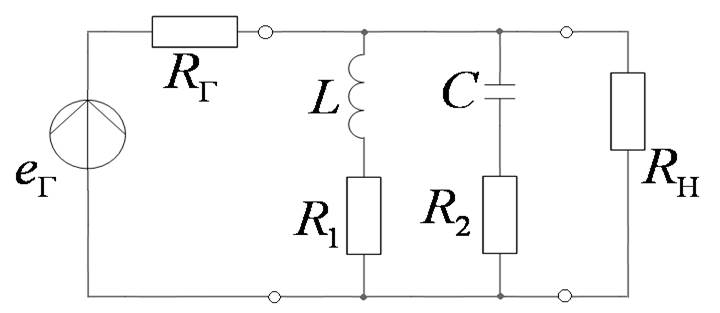
Эквивалентная схема контура
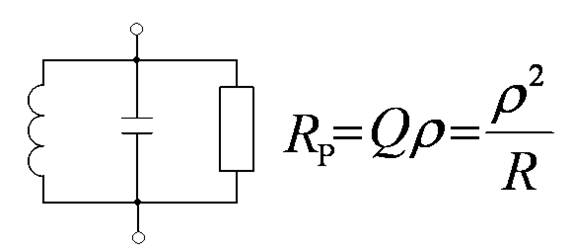
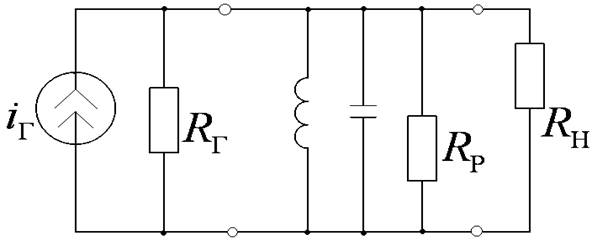
Добротность ненагруженного контура
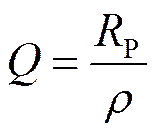
Для нагруженного контура
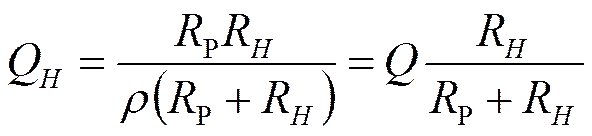

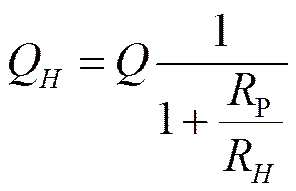
![]() Чем меньше Rн, тем ниже
добротность контура.
Чем меньше Rн, тем ниже
добротность контура.
Аналогично учитывается нагрузка слева, т.е.внутреннее сопротивление генератора.
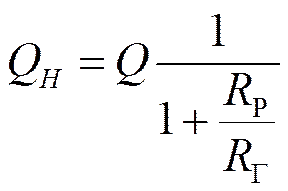
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.