Преобразования электрических схем
Типичные преобразования: а) последовательное соединение элементов
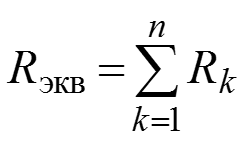
– резистивных элементов
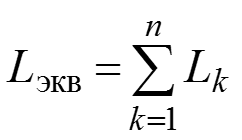
– индуктивных элементов
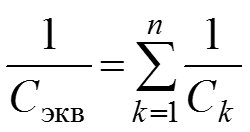
– емкостных элементов
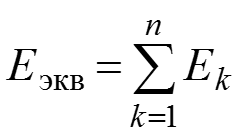
– источников напряжений
Источники тока последовательно не соединяются.
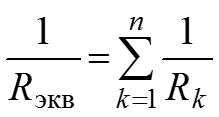
б) Параллельное соединение – резистивных элементов
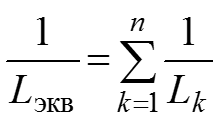
– индуктивных элементов
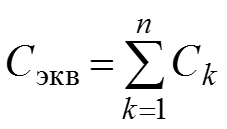
– емкостных элементов
.
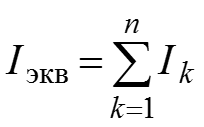
– источников тока
Замечание: соединение источников напряжения допустимо только для идентичных источников.
Преобразование «треугольника» в «звезду» и наоборот
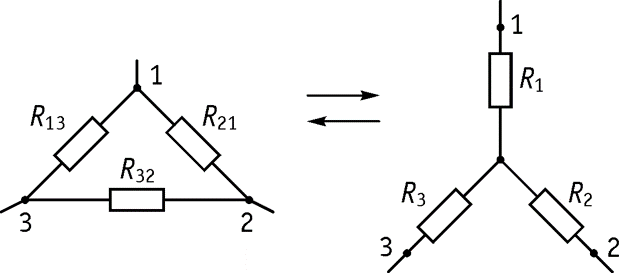
Преобразование из «треугольника» в «звезду»
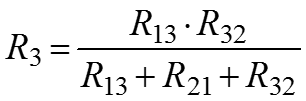
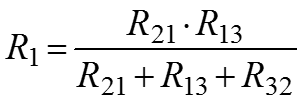
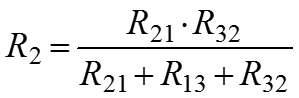
Преобразование из «звезды» в «треугольник»
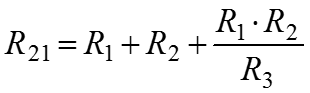
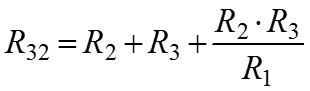
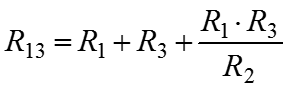
Преобразование реального источника напряжения в реальный источник тока (эквивалентные источники тока и напряжения)
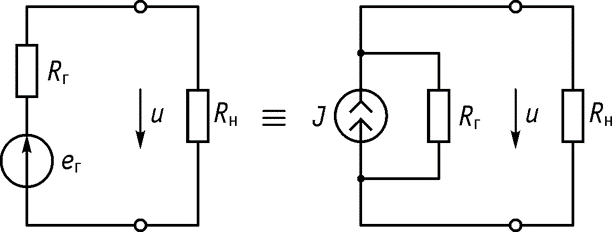
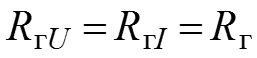
, то
Пусть имеется реальный источник ( рис.), если
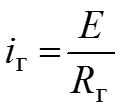
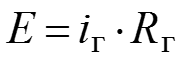
Эти соотношения можно получить, если воспользоваться принципом эквивалентности, т.е. токи и напряжения в непреобразованной части схемы остаются постоянными
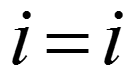
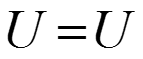
.
Методы расчета и анализа линейных электрических цепей в режиме постоянного тока
Расчет и анализ по законам Кирхгофа
Метод базируется на первом и втором законах Кирхгофа (ЗТК и ЗНК). Количество уравнений:
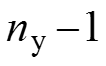
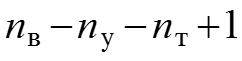
и
При составлении уравнений ЗНК нельзя выбирать контуры с источником тока. Контуры выбираются независимо друг от друга. Независимые контуры – это контуры, которые отличаются друг от друга хотя бы одной новой ветвью.
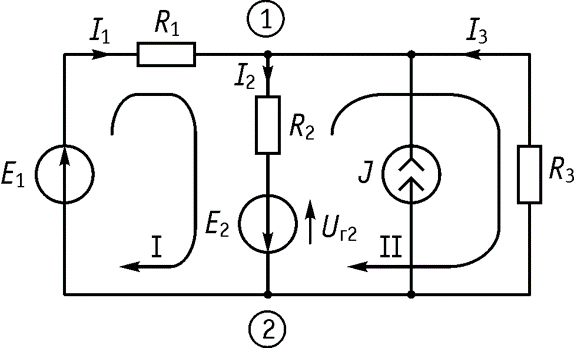
Пусть имеем электрическую схему, изображенную на рисунке. Алгоритм: 1. Обозначим узлы.
2. Обозначим токи в ветвях. 3. Выбираем независимые контуры. 4. Выберем направление обхода контура. 5. Составим
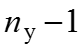
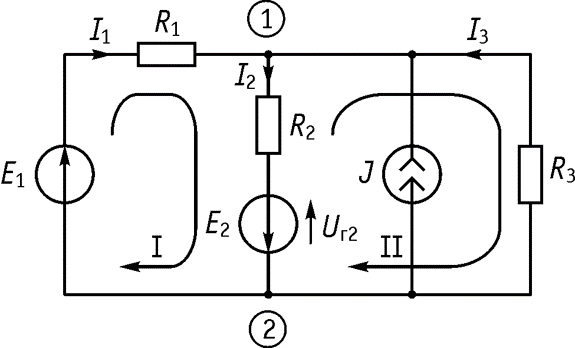
уравнений по ЗТК:
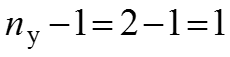
.
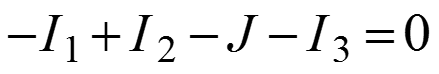
уравнений по ЗНК
![]()
6. Составим
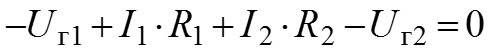
для контура I
![]()
для контура II
.
7. Система:
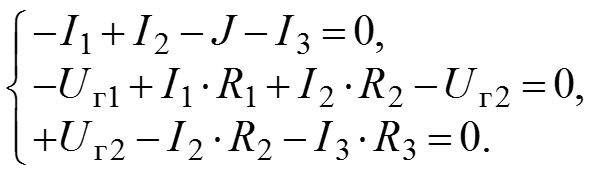
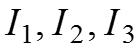
Решаем относительно независимых переменных
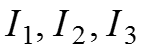
После определения токов
.
, определяем напряжение на элементах схемы
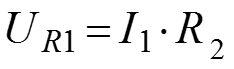
и т.д. Чтобы определить напряжение на зажимах источника тока, необходимо напряжение на источнике тока обозначить как U источника, направив в любом направлении.
Метод наложения
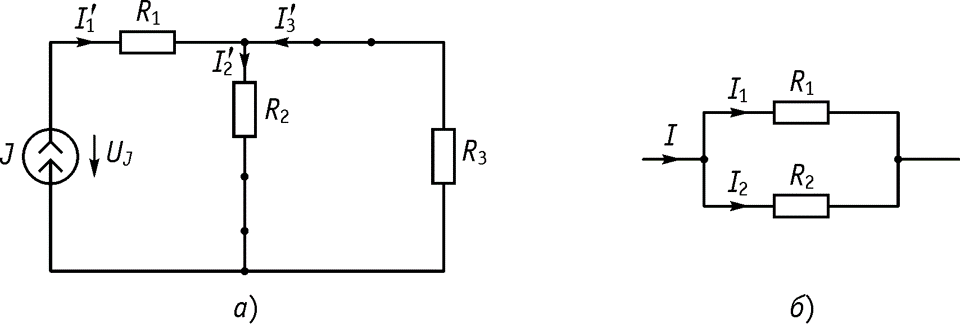
Пусть имеется цепь, приведенная на рисунке.
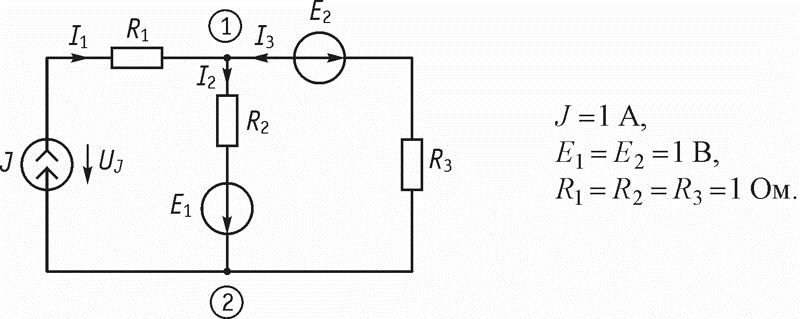
Необходимо определить токи и напряжения на элементах. Алгоритм: 1. Обозначаем узлы. 2. Обозначаем токи в ветвях. 3. Определяем частичные токи от одного воздействия.
![]()
Для этого: а) Удаляем из схемы источники напряжения (
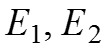
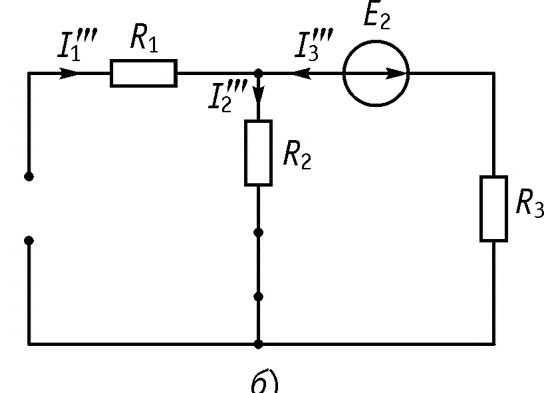
убираем совсем), а зажимы к которым были подключены источники напряжения соединяем вместе, т.е. замыкаем. б) Полученная схема приведена на рисунке
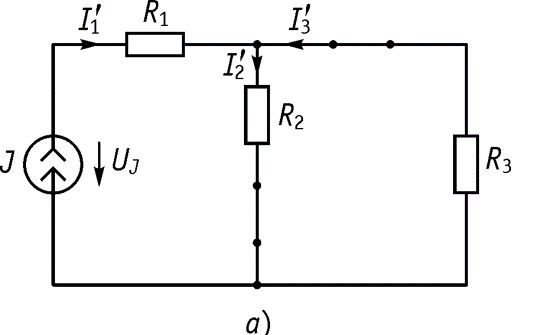
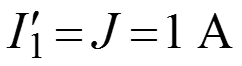
в) Определяем токи
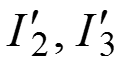
определяем по формуле разброса.
Формулы разброса (рис.б):
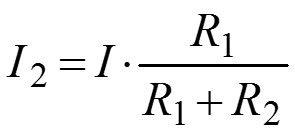
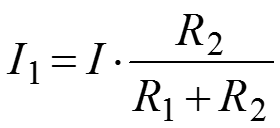
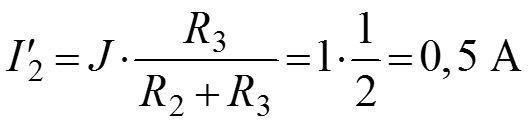
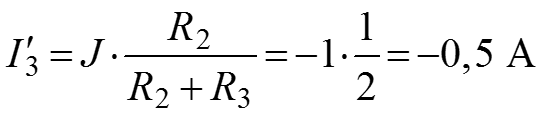
Далее: Убираем из схемы источники тока
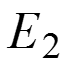
![]()
и
![]()
, оставляем разомкнутыми.
клеммы, к которым был подключен источник
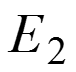
Клеммы, к которым был подключен
– замыкаем.
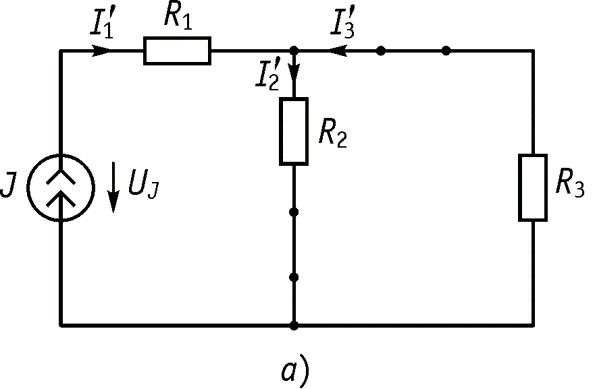
Полученная частичная схема приведена на рисунке
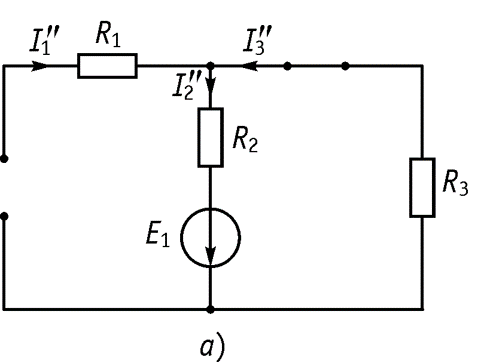
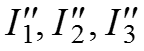
Определяем частичные токи
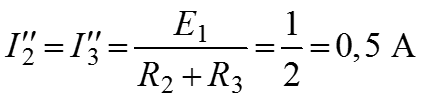
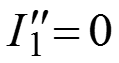
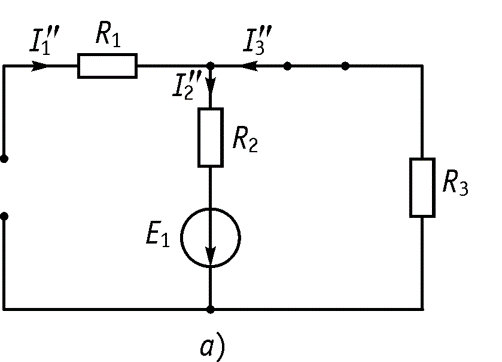
.
Далее: Убираем из схемы источники тока
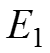
![]()
и
![]()
, оставляем разомкнутыми.
клеммы, к которым был подключен источник
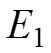
Клеммы, к которым был подключен
– замыкаем.
Полученная частичная схема приведена на рисунке
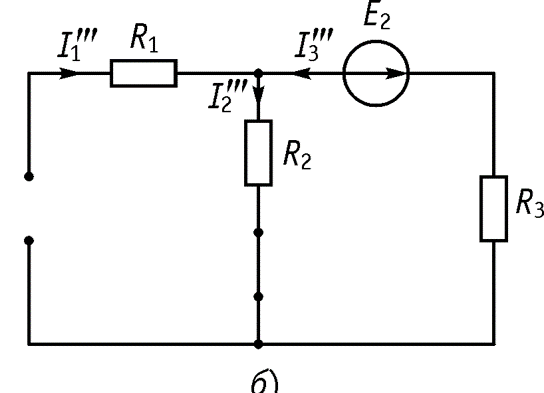
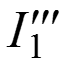
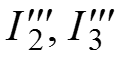
Определяем токи
,
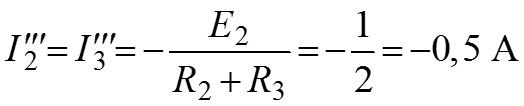
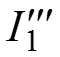
=0,
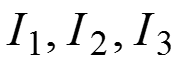
, как арифметическую сумму частичных токов
Определяем токи
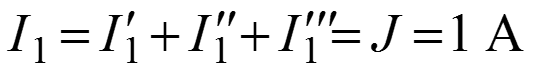
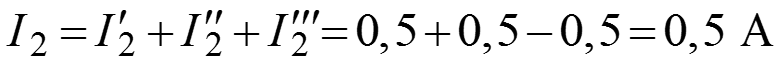
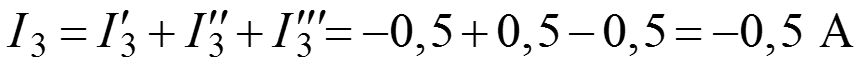
.
Определяем напряжения на элементах по закону Ома
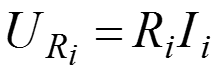
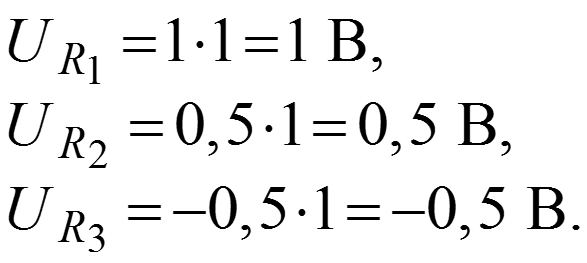
.
Определяем баланс мощности
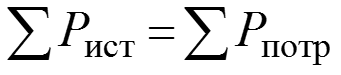
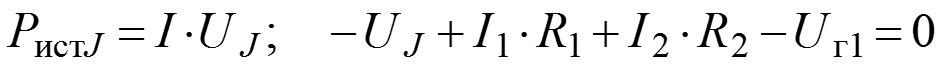
(Чтобы найти напряжение источника тока нужно взять контур с источником тока и по ЗНК записать уравнение.)
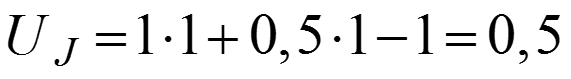
В.
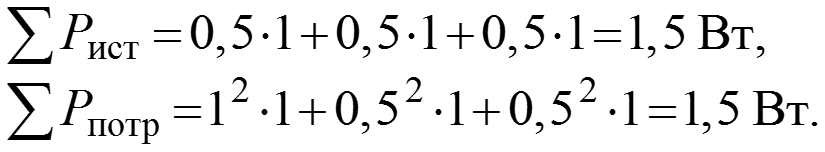
1,5 = 1,5 баланс выполняется, следовательно, расчет схемы выполнен верно.
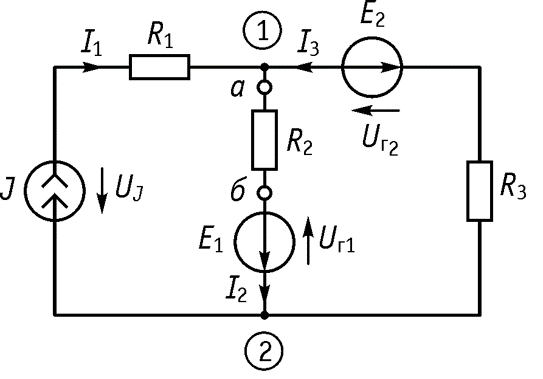
Метод эквивалентного генератора Метод базируется на теореме Тевенина и Нортона, позволяет упростить решение (анализ) задачи, связанной с передачей энергии от источника к определенному потребителю – приемнику. Пусть имеется цепь, приведенная на рисунке.
.
![]()
Требуется определить ток и напряжение, например, ток I2 в ветви
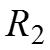
и напряжение на
Алгоритм анализа для метода эквивалентного генератора напряжения (А) 1. Обозначим токи в ветвях
![]()
![]()
2. Обозначим зажимы а и б, к которым подключено сопротивление
![]()
, напряжение между зажимами а и б обозначаем, как
3. Удаляем из схемы
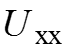
(напряжение холостого хода) и направляем его по направлению тока .
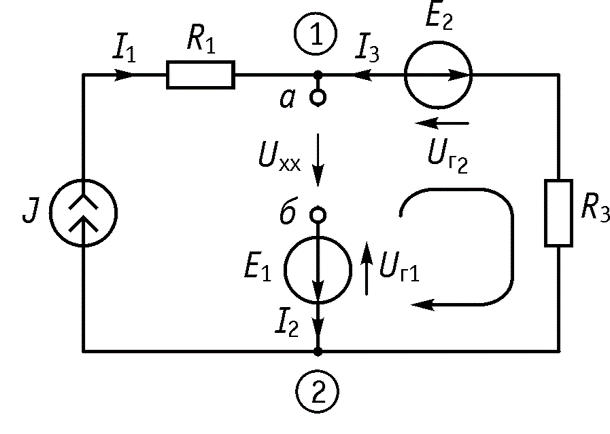
4. Определяем
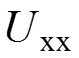
из уравнения ЗНК, составленного для контура, в котором нет источника тока

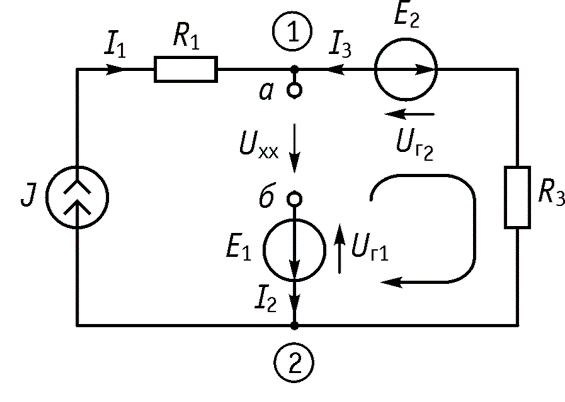
5. Определяем неизвестные токи:
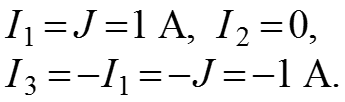
![]()
![]()
не существует, так как для источника
Тока в цепи от источника цепь имеет бесконечно большое сопротивление. 6. Определяем эквивалентное сопротивление цепи относительно разомкнутой ветви – зажимов а, б при удаленных источниках
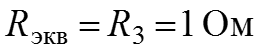
.
7. Представим схему относительно зажимов а и б в виде источника напряжения с задающим напряжением
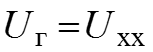
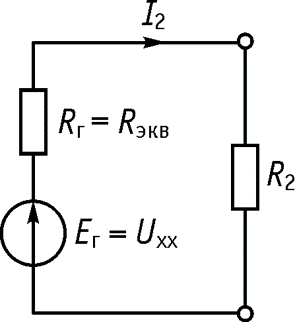
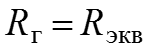
и внутренним сопротивлением
, а к клеммам источника подключим удаленное сопротивление
![]()
8. Определяем ток, протекающий через сопротивление R2
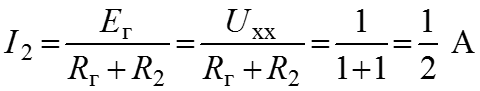
.
Метод узловых потенциалов (напряжений) Базируется на ЗТК и законе Ома, является наиболее распространенным методом, так как позволяет провести расчеты любых цепей на ЭВМ. Количество уравнений
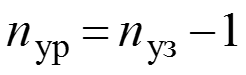
если нет ветви с идеальным источником напряжения (ветвь, которая содержит только источник) и
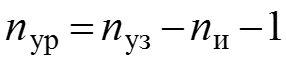
в противном случае.
Пусть имеется схема, приведенная на рисунке
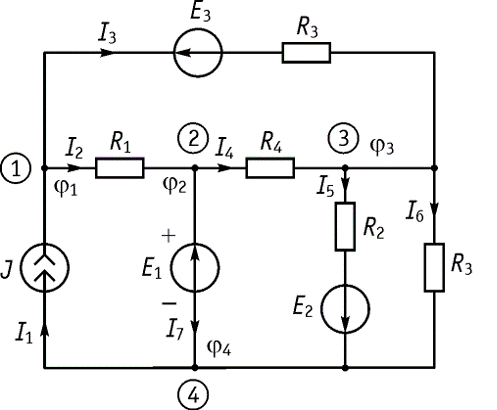
Необходимо определить токи в ветвях и напряжения на элементах.
Алгоритм метода: 1. Обозначаем узлы. 2. Обозначаем токи. 3. Обозначаем потенциалы узлов. 4. Выбираем базисный узел – такой узел, значение потенциала которого принимается равное нулю. При этом заметим:
а) если в схеме нет ветви с идеальным источником ЭДС, тогда в качестве базисного узла может быть выбран любой узел; б) если в схеме есть ветвь с идеальным источником напряжения (у нас это ветвь с источником
![]()
, тогда в качестве базисного узла принимается узел схемы, к которому подключен «минус» идеального источника ЭДС. При этом потенциал, к которому подключен «плюс» принимается, равным значению ЭДС) ( )
![]()
, а идеальный источник напряжения удаляется из схемы, при этом зажимы, к которым он был подключен, остаются разомкнутыми (рисунок ).
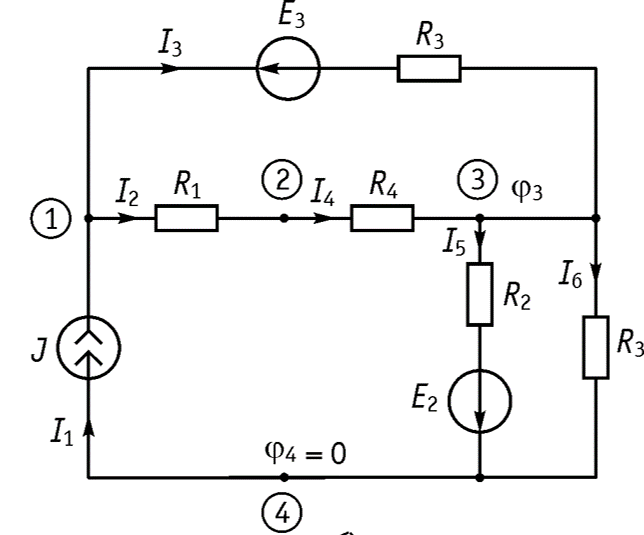
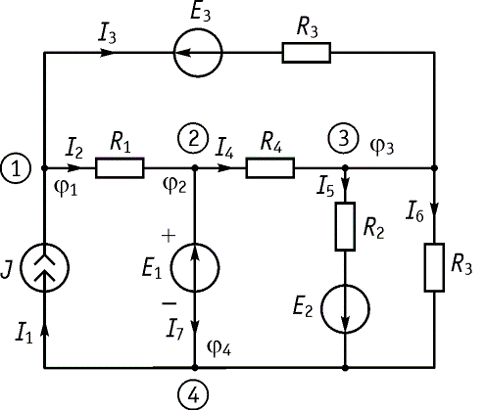
5. Составим уравнения по ЗТК для узлов 1-3
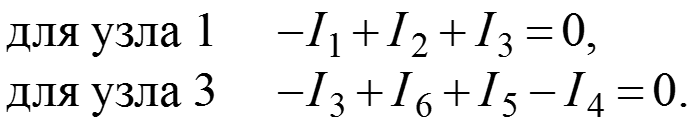
6. Определяем токи в ветвях через потенциалы узлов, используя закон
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.