ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Кафедра «Электрическая тяга»
Лабораторная работа №5
«Определение скорости начала хордового положения экипажа в кривой»
Выполнил студент
Группы: ЭТ-502
Рабинюк А.А.
Санкт-Петербург
2008
Цель работы- определение скорости начала хордового положения экипажа в кривой.
Условия: экипаж уже занял
в кривой хордовое положение, но направляющее усилие на последнюю (заднюю)
колёсную пару ещё отсутствует ![]() .Схемы положения
экипажа и действующие на последнюю (по ходу движения) колёсную пару сил,
представлены на рис.1.
.Схемы положения
экипажа и действующие на последнюю (по ходу движения) колёсную пару сил,
представлены на рис.1.
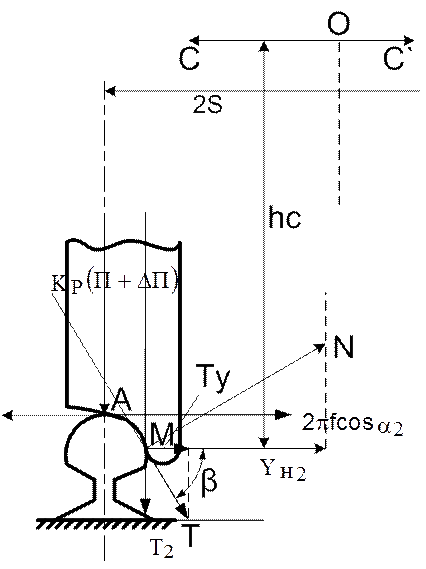
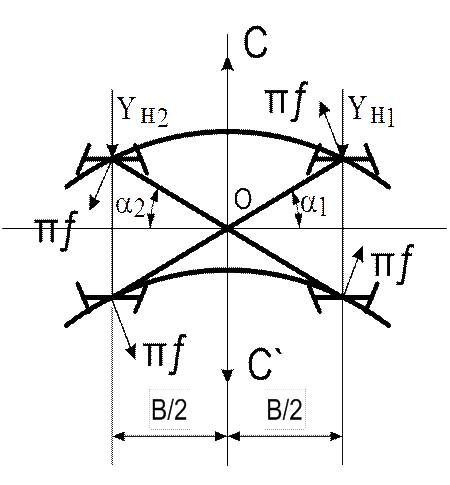
Рис. 1
В симметричных экипажах ![]() , соответственно:
, соответственно:
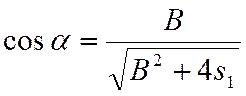
Для заднего (сбегающего) колеса уравнение равенства суммы сил приобретает вид:
![]() ;
;
Учитывая что:
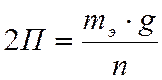 , кН,
, кН,
где ![]() - масса экипажа, приходящаяся на
одну тележку, т;
- масса экипажа, приходящаяся на
одну тележку, т;
n – число колёсных пар тележки;
g=9, 81 - ускорение свободного
падения, м/![]() .
.
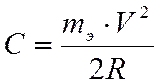 -
центробежная сила, действующая на экипаж, отнесённая к
-
центробежная сила, действующая на экипаж, отнесённая к
задней оси, кН,
где V – скорость движения экипажа, м/с;
R – средний радиус кривой, м.
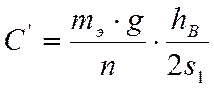 -
составляющая веса экипажа, уравновешивающая часть центробежной силы С, обусловленная
возвышением наружного рельса, кН,
-
составляющая веса экипажа, уравновешивающая часть центробежной силы С, обусловленная
возвышением наружного рельса, кН,
где ![]() - возвышение наружного рельса, м.
- возвышение наружного рельса, м.
![]() - расстояние между кругами катания
колёс с учётом уширения колеи в кривой,
- расстояние между кругами катания
колёс с учётом уширения колеи в кривой,
где ![]() - расстояние между кругами катания
колёс в прямых участках пути;
- расстояние между кругами катания
колёс в прямых участках пути;
e – уширение рельсовой колеи в кривой, зависящее от её среднего радиуса, м (см. лаб. работу №3).
![]() -
горизонтальная составляющая силы трения Т,
-
горизонтальная составляющая силы трения Т,
где ![]() - угол наклона образующей гребня
бандажа к горизонту в точке М;
- угол наклона образующей гребня
бандажа к горизонту в точке М;
![]() - коэффициенты трения бандажа о
поверхность головки рельса в точке М.
- коэффициенты трения бандажа о
поверхность головки рельса в точке М.
![]() - коэффициенты трения бандажа о
поверхность головки рельса в точке А.
- коэффициенты трения бандажа о
поверхность головки рельса в точке А.
В работе принять ![]() .
.
Подстановка значений
указанных величин в уравнении равновесия сил после несложных преобразований
позволяет получить следующие выражения для определения направляющего усилия ![]() :
:
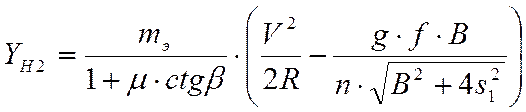 , кН
, кН
- без учёта возвышения наружного рельса (h=0),
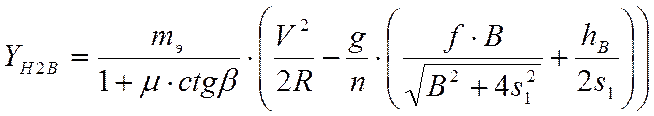 , кН
, кН
- с учётом возвышения наружного рельса (h≠0).
Нетрудно видеть, что ![]() (начало хордового положения) при:
(начало хордового положения) при:
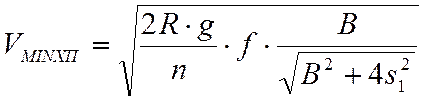 , м/с.
, м/с.
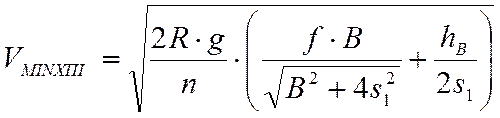 , м/с.
, м/с.
При всех ![]() >
>![]() экипаж будет занимать в кривой
заданного радиуса хордовое положение.
экипаж будет занимать в кривой
заданного радиуса хордовое положение.
Пример программы
f=0.25;
g=9.81;
n=2;
S1=0.79;
hv=0.1;
B=2.85;
R=150;
axis([2 8 15 60]);
hold on;
for I=1:5
B=2.85:0.1:8;
plot(B,sqrt(2*R*g/n*(f*B./sqrt(B.^2+4*S1^2)+hv/(2*S1))));
R=R+150;
end;
grid
ylabel('V,m/s');
xlabel('B,m');
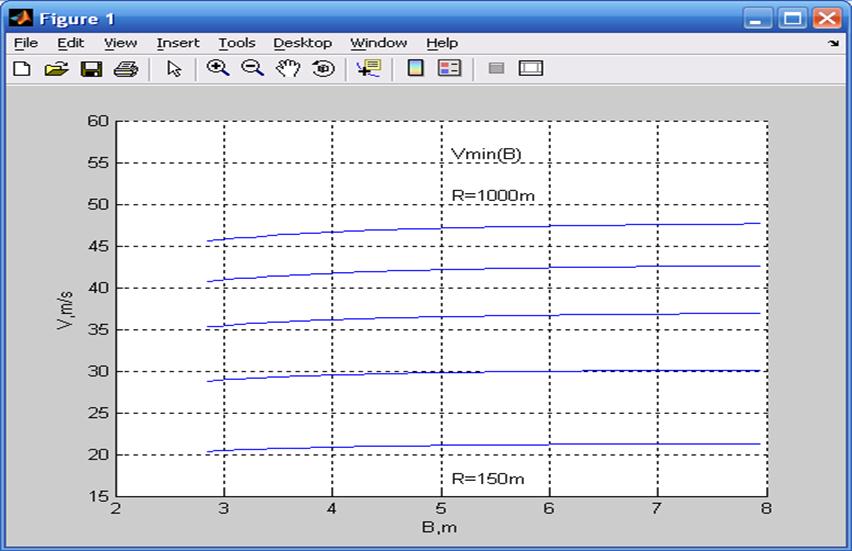
text(5.1,51,'R=1000m');
text(5.1,17,'R=150m');
text(5.1,56,'Vmin(B)');
pause
hold off;
clg;
B=2.85;
hv=0.1;
axis([150 3000 10 100]);
hold on;
for I=1:4
R=100:50:3000;
plot(R,sqrt(2*R*g/n*(f*B./sqrt(B.^2+4*S1^2)+hv/(2*S1))));
hv=hv+0.05;
end;
grid;
ylabel('V,m/s');
xlabel('R,m');
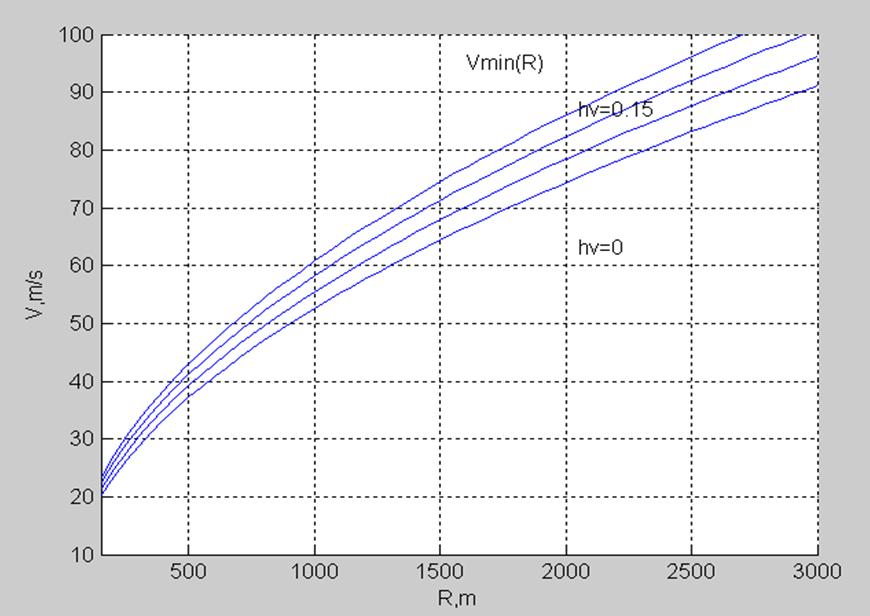
text(1600,95,'Vmin(R)');
text(2050,63,'hv=0');
text(2050,87,'hv=0.15');
hold off;
pause
clg;
Vcx = 22.3112
Vcxv = 22.3126
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.