Определение нормальных напряжений в точках поперечного сечения балки

Пример 3. Балка под действием распределенной нагрузки q, находящаяся на двух шарнирных опорах (рис.41).

z                       q

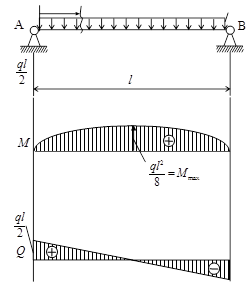
Рис.41

Равнодействующая распределенной нагрузки равна и приложена к середине балки. Вследствие симметричной нагрузки балки реакции опор равны между собой:

;

Изгибающий момент в сечении балки с абсциссой z равен:

Первое слагаемое – от реакции опоры (знак "+", поскольку выпуклость вниз);   второе слагаемое – от распределенной нагрузки слева от сечения (знак  «-», поскольку изгиб балки, условно закрепленной в сечении, выпуклостью вверх).

Данное уравнение является уравнением параболы. Вычислим три ординаты параболы для построения эпюры изгибающих моментов

 при z=0;  при  z=l/2;  при z=l.

Строим эпюру изгибающих моментов, учитывая, что максимум изгибающего момента находится в середине балки. Продифференцируем выражение для  и приравняем первую производную к нулю.

.

Из данного выражения видно, что максимум изгибающего момента при z=l /2:  .

Поперечную  силу в сечении определим как сумму внешних сил слева от сечения z:

;

; .

Стоим эпюру , обратив внимание, что , когда изгибающий момент  достигает максимума.

Пример 4. Построить эпюр идля консольно закрепленной балки, нагруженной двумя внешними парами  2М_е  и 3М_е (рис.42).

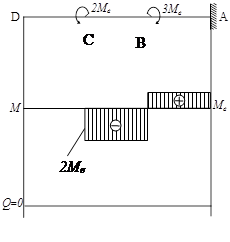Рис.42

Применяя метод сечений и используя приемы решения, рассмотренные выше, видим, что изгибающий момент на участке D-C равен нулю (сумма моментов сил слева от сечения равна нулю).

На участке C-B: .

На участке B-A: .

На всей длине балки  поперечная сила Q=0.

Пример 5. Построить эпюры внутренних силовых факторов для балки, представленной на рис.43.

Решая уравнения равновесия, определяем реакции опор:

 (направлена вниз);

 (направлена вверх).

Изгибающий момент в сечении  определяем как сумму моментов внешних сил слева от сечения:

 - уравнение параболы, где первое слагаемое от реакции опоры А, а второе слагаемое – от распределенной нагрузки q.

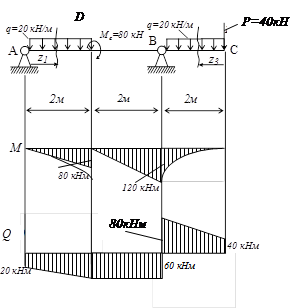Рис.43

Для построения кривой второго порядка вычислим три значения   величины изгибающего момента на участке z1:

   ;   

и по этим точкам строим  эпюру изгибающих моментов для участка A-D.

Изгибающий момент в сечении на расстоянии z2 определится из уравнения:

, где первое слагаемое – от реакции опоры;

второе – от распределенной нагрузки;

третье – от сосредоточенного момента.

Вычисляем два значения изгибающего момента:  и строим эпюру для участка D-B.

Изгибающий момент для участка B-C будем определять на расстоянии  от правого конца балки, поскольку легче вычислить сумму моментов сил справа от сечения:

, где:  первое слагаемое – от сосредоточенной силы Р;

второе – от распределенной нагрузки справа от сечения.

Определяем два крайних значения изгибающего момента на участке В-С :

;    

и строим эпюру изгибающих моментов.

Разрывы в эпюре изгибающих моментов наблюдаются в точках приложения сосредоточенных внешних моментов, а изменения угла наклона наблюдаются в точках приложения внешних сил.

Поперечные силы строим, используя зависимость  и проецируя на вертикаль силы, действующие на отсеченную часть:

.

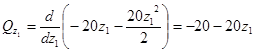Строим эпюру  как прямую для  и

На участке D-B эпюра  представляет собой прямую горизонтальную линию на уровне 60 кН.

При вычислении как производной от момента следует иметь в виду, что отсчитывается справа налево, поэтому для получения правильного знака  следует после дифференцирования сменить знак:

Строим эпюру поперечных сил для участка B-C.

Разрывы в эпюре  равны приложенным в соответствующих сечениях балки сосредоточенным силам: реакциям  и , а также силе  на конце балки.

Пример 6. Построить эпюры внутренних силовых факторов для ломаной консольно закрепленной балки, нагруженной сосредоточенной силой Р  (рис.44).

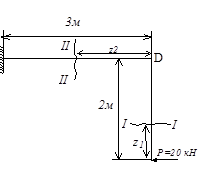
Рис.44

Необходимо условиться о правиле построения эпюр для вертикальных и наклонных стержней. Обычно эпюру изгибающих моментов  принято строить на вогнутой стороне стержня (на сжатом волокне), т.е. также, как и для горизонтальных стержней.

Изгибающий момент в сечении I-I, как сумма моментов внешних сил, расположенных по одну сторону от сечения (снизу)  (выпуклость справа, сжатое волокно слева). Строим эпюру изгибающих моментов слева. При z₁ =0  =0, а при  z₁ =2м  =40 кНм.

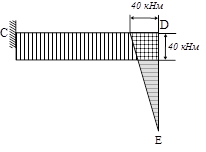
Изгибающий момент в сечении П-П, как сумма моментов внешних сил, расположенных справа от сечения, равен произведению силы Р на плечо DE: . Эпюра изгибающих моментов для участка С-D строится на нижней стороне балки.

Поперечную силу Q определяем по формуле: , т.е. вычисляем ее как тангенс угла наклона касательной к эпюре моментов.

Для стержня CD -  M_и=const, следовательно Q=0.

Для стержня DE -  M_b=Pz₁, следовательно, Q=P. По полученным значениям поперечной силы строим эпюру поперечных сил.