15. Потенциальная энергия деформации при изгибе.
При изгибе, также как и при других видах деформации, работа, производимая внешними силами, затрачивается на изменение потенциальной энергии деформированного стержня.
Работа внешнего момента при упругой деформации стержня:
![]() , где
, где ![]() - угол
поворота сечения в точке приложения момента.
- угол
поворота сечения в точке приложения момента.
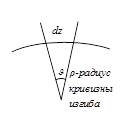
Элементарная работа изгибающего (внутреннего) момента определяется из выражения (по аналогии со случаем растяжения-сжатия):
![]() , но при изгибе
имеем:
, но при изгибе
имеем: ![]() .
.
Кривизна, как величина, обратная радиусу кривизны ![]() определяется из выражения:
определяется из выражения:
![]() , где:
, где: ![]() - модуль упругости первого рода;
- модуль упругости первого рода;
![]() - момент
инерции сечения относительно нейтральной оси сечения.
- момент
инерции сечения относительно нейтральной оси сечения.
Поэтому можно записать:
![]() .
.
Полная работа изгибающих моментов для балки длинной l:
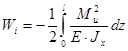 .
.
Потенциальная энергия изгиба, равная работе внутренних сил, взятая с обратным знаком, определяется из выражения:
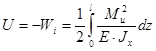 .
.
Добавок потенциальной энергия за счет сдвига (для общего случая не прямого, а поперечного изгиба), соответствует работе поперечной силы. Но этот добавок по абсолютному значению невелик и при практических расчетах им обычно пренебрегают.
16. Теорема о взаимности работ и взаимности перемещений.
Рассмотрим упругую линейно деформируемую систему в двух различных состояниях, отвечающих двум различным нагрузкам P1 и P2 (рисунок 47). В данном случае простая балка нагружена в обоих состояниях простой нагрузкой (по одной сосредоточенной силе P1 и P2).
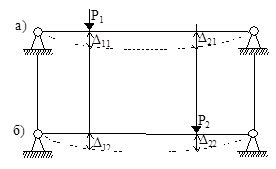
Рисунок 47
а) первое состояние системы (под нагрузкой Р1);
б) второе состояние системы (под нагрузкой Р2).
Δ11 – перемещение по направлению нагрузки Р1 в месте ее приложения от действия Р1.
Δ21– перемещение по направлению нагрузки Р2 в месте ее приложения от действия Р1.
Δ22 – перемещение по направлению нагрузки Р2 в месте ее приложения от действия Р2.
– перемещение по направлению нагрузки Р1 в месте ее приложения от действия Р2.
Перемещения Δ11 к Δ22 называются главными, а перемещения Δ12 к Δ21 – побочными.
Теорема: Работа внешних сил первого состояния, на перемещениях, вызванных силами второго состояния, равна работе внешних сил второго состояния на перемещениях, вызванных силами первого состояния.
Доказательство.
1) Вначале приложим силу Р1, а затем к деформированной балке приложим силу Р2.
Подсчитаем работу, произведенную внешними силами (обращая внимание на рисунок 48).
Работа произведенная статически приложенной силой Р1 на собственном перемещении Δ11, вызванном этой силой, определится из выражения:
![]() .
.
Работа, произведенная статически приложенной силой Р2 на собственном перемещении Δ22 определится из подобного выражения:
![]() .
.
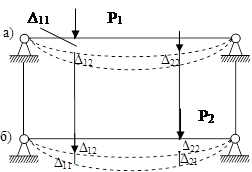 |
Рисунок 48
При этом дополнительная работа уже постоянно приложенной силы Р1 на перемещении Δ12, вызванном силой Р2 определится из выражения:
![]() ,
,
(обращая внимание на то, что множитель 1/2 в выражении отсутствует, поскольку сила Р1 постоянна на перемещении Δ12).
Полная работа внешних сил при рассмотренной последовательности приложении нагрузок:
![]() .
.
2) Теперь вначале приложим силу Р2, а затем к деформированной системе приложим силу Р1.
Рассуждаем аналогично первому случаю. Работа произведенная силой Р2 на собственном перемещении Δ22, вызванном этой силой:
![]() .
.
Работа, произведенная силой P1 на собственном перемещении Δ11:
![]() ;
;
Дополнительная работа силы P2 на перемещении Δ21, вызванном силой P1:
![]()
(множитель 1/2 отсутствует, поскольку сила P2 постоянна на перемещении Δ21).
Тогда полная работа внешних сил при рассмотренной последовательности приложения нагрузок:
![]() .
.
Поскольку работа сил не зависит от порядка их приложения, следовательно:
![]() ,
,
или иначе:
![]() , а для рассматриваемого случая;
, а для рассматриваемого случая;
![]() .
.
Полагая приложенные силы единичными P1= P2=1, получим равенство перемещений, вызванных единичными силами:
δ 12=δ 21
Последнее равенство доказывает теорему о взаимности перемещений:
Перемещение точки приложения единичной силы по ее направлению, вызванное второй единичной силой, равно перемещению точки приложения второй единичной силы по направлению последней, вызванному действием первой единичной силы.
Аналогично можно доказать взаимность дополнительной работы внутренних сил:
![]() .
.
Для этого рассмотрим элемент балки длиной dz (рисунок 49).
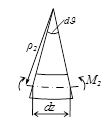
Рисунок 49
При нагружении балки силой Р1 в ее поперечном сечении
возникает изгибающий момент М1. Для элемента балки длинной dz
дополнительная работа внутренних сил (момента ![]() на
угловом перемещении
на
угловом перемещении ![]() , вызванном моментом
, вызванном моментом ![]() ):
):
![]() .
.
Учитывая, что ![]() и поскольку
и поскольку ![]() , то
, то ![]() , поэтому:
, поэтому:
![]() .
.
Дополнительная работа внутренних сил для всей длины балки l:
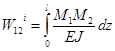 .
.
где ![]() ,
,![]() - текущие значения
изгибающих моментов в первом и втором состояниях.
- текущие значения
изгибающих моментов в первом и втором состояниях.
Аналогично рассуждая, можно показать, что: 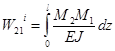 .
.
Следовательно:
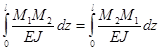 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.