Потенциальная энергия деформации при изгибе. Теорема о взаимности работ и взаимности перемещений, страница 2

Исходя из закона сохранения энергии, можно показать, что дополнительная работа внешних сил равна по абсолютному значению дополнительной работе внутренних сил:

.

При нагружении системы силой Р₁ внешние силы совершают работу , а внутренние силы совершают работу .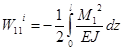

В силу закона сохранения энергии можно записать равенство:

.

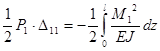При нагружении системы силой Р₂ по аналогии можно показать:

.

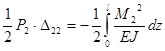Кроме того, при нагружении системы силой Р₂ совершается дополнительная работа внешней силы Р₁:

.

А дополнительная работа, совершаемая внутренними силами (изгибающими моментами):

.

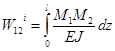На основании закона сохранения энергии должно быть:

 и

;

и следовательно:

.                                         (*)

17. Определение перемещений методом Мора. Правило Верещагина.

Предположим, что мы имеем балку, нагруженную сосредоточенной силой Р и распределенной нагрузкой произвольной конфигурации. Данное состояние балки представлено на рисунке 50 и обозначено как грузовое состояние f. Далее предположим, что требуется вычислить вертикальное перемещение т.В. Для решения данной задачи введем вспомогательное состояние балки, в котором приложим к балке единичную силу 1 в интересующей нас т.В (вспомогательное состояние балки k).

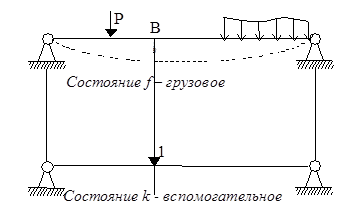
Рисунок 50

Для решения поставленной задачи вычислим работу внешних и внутренних сил вспомогательного состояния на перемещениях, вызванных действием сил грузового состояния.

Работа внешних сил равна произведению единичной силы на искомое перемещение .

.

А работа внутренних сил определяется выражением:

.

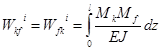В силу равенства дополнительной работы внутренних и внешних сил можем записать:

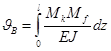 - формула Мора.

В соответствии с данной формулой для определения перемещения т.В необходимо записать аналитически изгибающий момент грузового состояния и изгибающий момент вспомогательного состояния, подставить эти выражения в формулу Мора и проинтегрировать по всей длине балки.

Если  и  имеют одинаковые знаки, то произведение положительно, а это будет означать, что перемещение интересующей нас точки будет совпадать с направлением приложенной единичной силы.

Если требуется определить угловое смещение сечения в точке B, то в вспомогательном состоянии k следует приложить в точке B сосредоточенный момент,  равный единице (без размерности). Результат интегрирования даст нам угловое смещение сечения.

Определяя через Δ любое перемещение (линейное или угловое) интеграл Мора запишем в виде:

.                                                         (**)

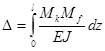Аналитические выражения  и  могут быть различными на разных участках упругой системы, тогда интегрирование ведем раздельно для различных участков, а результаты суммируем по всем участкам:

.

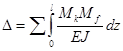Если стержни работают на изгиб и растяжение, то перемещение определится суммой:

.

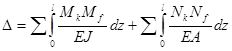Практически обычно учитывают только первое слагаемое, поскольку второе мало.

Вместо вычисления интеграла Мора (**) для определения перемещений можно воспользоваться графоаналитическим приемом перемножения эпюр, который называется правилом Верещагина.

Сущность метода заключается в следующем. Рассмотрим две эпюры изгибающих моментов  (рисунок 51), из которых одна (рисунок 51-а) грузовая (эпюра изгибающих моментов  имеет произвольное очертание). Другая  (рисунок 51-б) вспомогательная (эпюра изгибающих моментов - прямолинейная). Вспомогательная эпюра строится для случая, когда в интересующей нас точке балки приложена единичная сила. Сечение балки на участке BD считаем постоянным.

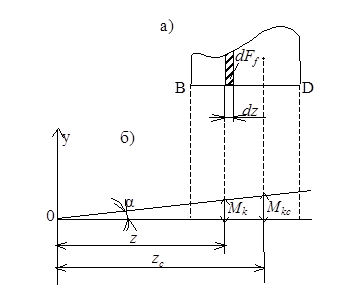
Рисунок 51

В этом случае постоянные величины вынесем за знак интеграла:

.

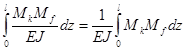Величина  - элементарная площадь  грузовой эпюры , следовательно:

;

Но , следовательно .

Но  - статический момент площади эпюры  относительно оси O-y, равный:

, где  - площадь грузовой эпюры моментов;

 - расстояние от оси O-y до центра тяжести площади грузовой эпюры .

Но с другой стороны:

, где  - ордината вспомогательной эпюры , расположенная под центром тяжести грузовой эпюры  (под точкой C), следовательно:

, т.е. искомый интеграл равен  произведению площади грузовой эпюры  (любой по очертанию) на расположенную под ее центром тяжести ординату вспомогательной (обязательно прямолинейной) эпюры .

Окончательно для оценки перемещения произвольной точки получаем:

.

 - величина положительная, если обе эпюры расположены по одну сторону стержня. Положительный результат говорит о том, что направление перемещения совпадает с направлением вектора единичной силы.

 - ордината должна браться (обязательно) из прямолинейной эпюры.

Для упрощения расчетов величины деформации балки в интересующей нас точке грузовую эпюру следует расчленить на простейшие фигуры (прямоугольники, треугольники и т.п.). Перемножение эпюр следует производить для этих элементарных участков, а после сложения полученных результатов перемножения будет определена и деформация балки в интересующей нас точке.