Опытным путём установлена зависимость, которая выражает закон Гука при сдвиге: величина угловой деформации γ при сдвиге прямо пропорциональна касательному напряжению:
, где G – коэффициент модуль упругости
второго рода (модуль сдвига).
Связь между модулем сдвига G и модулем упругости первого рода Е определяется зависимостью:
, где ν
– коэффициент Пуассона.
Стержень испытывает кручение, если в его поперечных сечениях возникают крутящие моменты. Таким образом нагруженные стержни называют валами.
Внешние скручивающие моменты Ме и внутренние крутящие моменты МКР изображаются в виде линии с двумя кружочками (рис.24). Для определения крутящих моментов МКР, возникающих в сечениях вала под действием внешних скручивающих моментов, будем применять метод сечений. Мысленно рассечем вал плоскостью а-а и отбросим, например, левую часть.
Взаимодействие частей стержня по линии разреза заменяем
крутящим моментом Мкр. Для равновесия отсечённой (оставшейся)
части необходимо, чтобы суммы всех моментов, действующих на неё, была равна
нулю. Отсюда 
или 
.
В общем случае крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения.
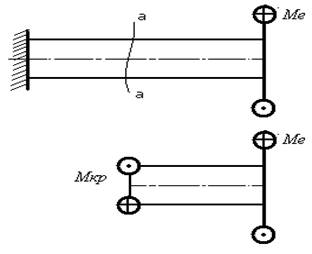
Рис.24
Принимаем, что крутящий момент в сечении а-а считается положительным, когда внешний момент вращает отсечённую часть по часовой стрелке, если смотреть на отсечённую часть со стороны сечения (рис.25).
 |
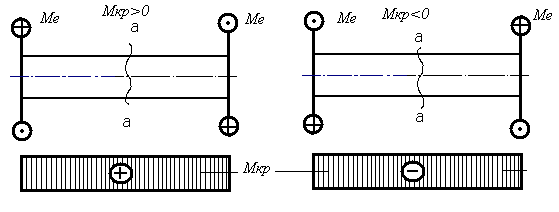Для установления закона распределения касательных напряжений по поперечному сечению скручиваемого стержня рассмотрим деформации стержня при кручении.
На рис.26 изображена часть стержня, подвергаемого скручиванию, длиной dz.
Угол
сдвига на поверхности: 
.
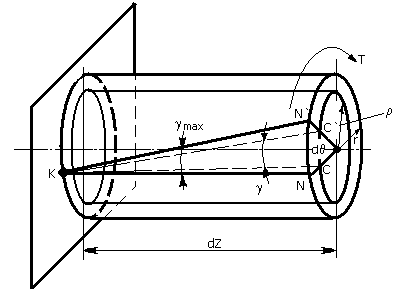
Угол сдвига для элемента, отстоящего на расстоянии ρ от оси стержня:
.
На основании закона Гука при сдвиге имеем:
, (*)
т.е. при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.
Наибольшие касательные напряжения будут в точках сечения, расположенных у поверхности стержня. В центре тяжести круглого сечения касательные напряжения равны нулю (рис.27).
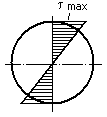
Рис.27
Крутящий момент в сечении представляет собой равнодействующий момент касательных напряжений в сечении:
(**)
где 
– элементарный
крутящий момент внутренних сил, действующих на площадке dF.
Подставив выражение (*) в (**), получим:
.
Имея в виду, что 
–
полярный момент инерции сечения, получим:
.
Подставив данное выражение в уравнение (*), получим:
.
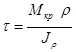Из полученного соотношения видно, что в одинаково удалённых от центра сечения точках напряжения τ одинаковы. В точках, находящихся на внешней поверхности сечения, касательные напряжения достигают максимального значения:
, где 
– геометрическая характеристика
сечения, называемая полярным моментом сопротивления или моментом сопротивления
сечения при кручении.
Для круглого сплошного сечения моментом сопротивления сечения:
.
Аналогично для кольцевого (трубного) сечения:
, где 
.
Условие статической прочности вала при кручении записывается в виде:
(***), где [τ] – допустимое касательное напряжение для выбранного материала.
При действии статической нагрузки часто принимают: 
, где 
-
допустимое напряжение при растяжении-сжатии.
С помощью выражения (***) можно подобрать диаметр вала
dили определить
допустимый крутящий момент 
при известных
остальных величинах.
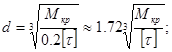
11. Деформации и перемещения при кручении валов.
Для вычисления деформаций воспользуемся выражением:
.
Полную угловую деформацию вала на длине z получим после интегрирования данного выражения:
.
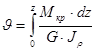Для однородного вала: 
,
а для вала длиной l: 
.
Относительный угол закручивания на единицу длины: 
.
Для обеспечения требуемой жесткости необходимо, чтобы угол закручивания не превосходил допустимого:
, или 
.
Для валов средних размеров (до 400 мм) допустимый
угол закручивания обычно принимают 
.
11. Потенциальная энергия упругой деформации при кручении.
Но в некоторых случаях можно раскрыть статическую неопределимость, используя условия нагружения валов.
Пример: Построить эпюры крутящих моментов и угловых деформаций вала, имеющего глухую заделку с обоих концов и нагруженного внешним скручивающим моментом Ме (рис.28)
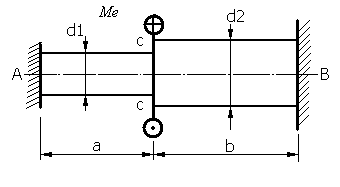
Рис.28
Такой стержень, имеющий глухую заделку с двух сторон и нагруженный скручивающим моментом Ме, статически неопределим, так как для нахождения двух реактивных моментов, возникающих в заделках, статика даёт лишь одно уравнение равновесия.
Для решения данной задачи поступим следующим образом. Отбросим одну заделку, например, правую, заменив её действие неизвестным моментом Х (рис.29).
Составим уравнения возможных перемещений, учитывая, что угол поворота
сечения у отброшенной заделки под действием моментов Ме и Х
равен нулю 
.
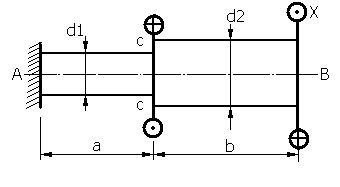
Рис.29
Определим угол закручивания сечения вала в правой заделке:
– угол
поворота сечения В под действием одного момента Х.
– угол
поворота сечения В под действием одного скручивающего момента Ме.
Суммарный угол поворота по условию задачи равен нулю, следовательно:
Из данного уравнения определяем реактивный момент Х и, используя ме тод сечений, определяем крутящий момент на различных участках вала и строим эпюру крутящих моментов Мкр (рис.30).
Для построения эпюры углов закручивания сечений вала 
вычислим угол поворота сечения с-с
при движении от заделок справа и слева.
.
Углы поворота сечений А и В равны нулю,
а т.к. угол поворота линейно зависит от расстояния 
,
то полученные точки эпюры соединяем прямыми.
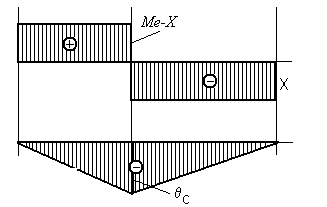
Эпюра Мкр
Эпюра углов закручивания сечений вала
Таким образом, полученные при рассмотрении вопросов кручения валов результаты позволяют сказать, что наиболее рациональными сечениями, обеспечивающими максимум допускаемого крутящего момента при одинаковом расходе материала, являются сечения круглые, особенно кольцевые при малой толщине стенок. Наименее выгодные сечения – швеллеры, двутавры и другие прямоугольные сечения. Данный вывод проистекает из того факта, что требуется обеспечивать при одинаковой площади поперечного сечения как можно большее значение полярного момента сопротивления Wρ (или Wt для некруглого сечения).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
