Изгиб. Определение опорных реакций. Правила знаков для поперечных сил и изгибающих моментов

12. Изгиб

Очень часто стержни  подвергаются действию поперечных сил и внешних пар (рис.31). Под действием таких нагрузок ось стержня искривляется. При этом в поперечных сечениях стержня возникает изгибающие моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.

Рис.31

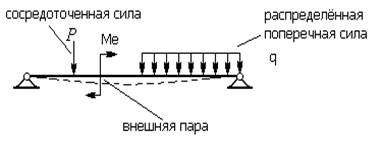
Указанный вид нагружения называют изгибом, а стержни, работающие на изгиб, называют балками. Если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня, то изгиб называют чистым.

Изгиб называют поперечным, если наряду с изгибающими моментами возникают также и поперечные силы.

Если плоскость действия изгибающего момента проходит через одну из главных центральных осей поперечного сечения стержня, изгиб называют прямым (простым или плоским), в противном случае косым.

12.1. Типы опор балок.

1.  Подвижная шарнирная опора.

В данной опоре ограничено перемещение вверх-вниз, поэтому в ней присутствует  только одна реакция, перпендикулярная плоскости качения.

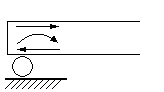
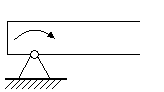
2. Неподвижная шарнирная опора.

В данной опоре ограничено перемещение как вверх-вниз, так и вправо-влево, поэтому в ней присутствует  реакция, которую обычно представляют в виде двух составляющих: горизонтальной и вертикальной.

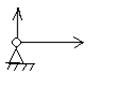
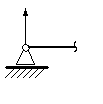
3.  Жёсткая заделка.

Заделка не допускает ни линейных, ни угловых перемещений. Реакцию заделки обычно раскладывают на две составляющие и реактивный момент.

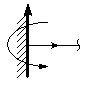
4.   Шарнир.

Шарнир допускает угловое перемещение, поэтому реакцию шарнира представляют в виде двух составляющих: вертикальной и горизонтальной

Если опорные реакции конкретной балки могут быть найдены из одних уравнений статики, то балки называют статически определимыми. Если же число опорных реакций больше, чем число уравнений статики, то балки называют статически неопределимыми

12.2. Определение опорных реакций.

Пример 1. Определить реакции опоры консольно закрепленной (глухо заделанной) балки (рис.32). Балка нагружена сосредоточенной силой Р1  и распределенной силой q.

Для определения опорных реакций необходимо мысленно отбросить опоры, заменив их соответствующими реакциями.

В данном случае реакцию заделки имеем в виде силы,  представленной двумя векторами А_у и А_z , и реактивного момента М_А.  Составляем уравнения равновесия балки:

Рис.32

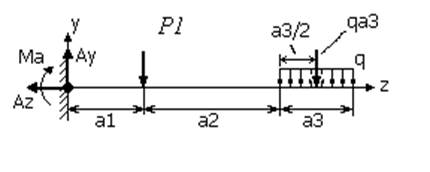
сумма сил на ось Xравна нулю, сумма сил на ось Yравна нулю и сумма моментов относительно любой точки балки равна нулю.

; .

; ;  , где - равнодействующая распределенной нагрузки q, точка приложения которой находится на середине участка балки а3.

; (сумма моментов относительно точки заделки балки) , откуда , т.е. направление реактивного момента следует поменять на обратное, поскольку результат получился со знаком минус.

Пример 2. Определить реакции опор балки, представленной на рис.33. Балка нагружена сосредоточенной силой Р, распределенной силой q и сосредоточенным моментом Ме.

  

Рис.33

Поступаем также как и в предыдущем примере, т.е. мысленно отбрасываем опоры, заменяя их реакциями опор, и составляем уравнения равновесия:

;  ;;

;

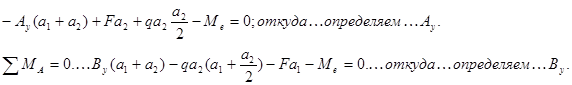
Вместо последнего уравнения можно использовать условие  поскольку значение А_у уже найдено. Тогда из выражения  определяем В_у.

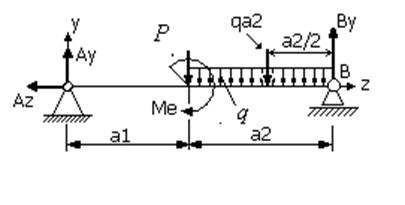
Пример 3.  Определить реакции опор балки, представленной на рис.34 и нагруженной сосредоточенной силой Р.

Рис.34

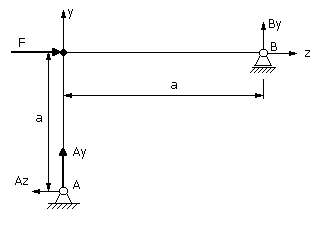
Поступаем также как и в предыдущем примере, т.е. мысленно отбрасываем опоры, заменяя их реакциями опор, и составляем уравнения равновесия:

; ; откуда ;

; ;  ;

; ; .

Знак минус для  реакции А_у говорит о том, что направление данной реакции в противоположную сторону относительно выбранному на чертеже.

Для проверки решения можно воспользоваться условием .

12.3. Определение внутренних усилий в балках.

Внутренние усилия (силовые факторы) в поперечных сечениях балки: изгибающий момент М_и и поперечная сила Q.

Предположим, что мы имеем балку, нагруженную двумя сосредоточенными силами Р₁ и  Р₂ (рис.35). Прежде всего, необходимо определить реакции опор, для чего можно применить рассмотренные выше приемы.

Для определения внутренних силовых факторов применим метод сечений, для чего в интересующем нас месте сделаем мысленный разрез балки на расстоянии z и отбросим одну часть, например правую.

Рис.35

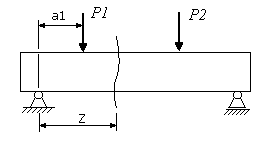
Затем рассмотрим равновесие левой части, заменив левую опору ее реакцией А.

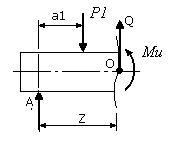
Взаимодействие частей балки заменим внутренними усилиями: изгибающим моментом М_и и поперечной силой Q.

Уравнения равновесия (сумма сил на вертикальную ось y и сумма моментов