Основы конструирования радиоэлектронных систем. Напряжения: полное, нормальное и касательное

ОСНОВЫ КОНСТРУИРОВАНИЯ РЭС

(Курс лекций)

ВВЕДЕНИЕ

При разработке конструкции современных радиоэлектронных систем (РЭС) приходится решать большое число различных проблем как схемотехнического, так и конструкторского характера. А при необходимости решения задач конструирования не последнее место занимают задачи расчетов на механическую прочность узлов и деталей. Поэтому очевидно, что для этого необходимо знание основных методов расчета конструкций на прочность. Целью настоящего лекционного материала дать студентам необходимые знания из области сопротивления материалов для применения их при расчетах на прочность наиболее распространенных видов конструктивных элементов.

1.  Основные определения сопротивления материалов.

Практика конструирования РЭС показывает, что большое разнообразие различных элементов конструкций может быть сведено к небольшому количеству простейших расчетных схем, в которых рассматриваются упругие тела вполне определенной формы: брус, пластина, оболочка.

Брусом (стержнем) называется призматическое или цилиндрическое тело, у которого длина значительно превышает размеры поперечного сечения. Ось бруса – это линия, проходящая через центр тяжести его поперечного сечения. Брус может быть прямым и кривым.

Пластиной (оболочкой) называется твердое тело, имеющее весьма малую толщину по сравнению с двумя другими ее размерами.

Внешними силами называются все силы, приложенные к телу извне. Они могут быть как сосредоточенными, так и распределенными.

По времени действия различают нагрузку постоянную и временную, статическую (медленно изменяющуюся) и динамическую (удар).

В сопротивлении материалов изучают упругое тело, т.е. устанавливается связь между изменениями размеров или формы тела и внешними силами.

Тело, обладающее свойствами полностью восстанавливать свою геометрическую форму и размеры после снятия нагрузки, называется упругим. Свойство тела не восстанавливать своей первоначальной формы после снятия нагрузки называется пластичностью.

Изменение формы тела и его размеров под действием внешних сил называется деформацией. Часть деформации, которая исчезает после снятия нагрузки на тело, называется упругой, а часть, которая не исчезает, называется остаточной деформацией.

2. Напряжения: полное, нормальное и касательное.

Рассмотрим покоящееся тело (рис.1), на которое воздействуют внешние силы . В этом случае все внешние силы, действующие на тело, находятся в равновесии, поэтому и каждая отдельная часть тела также находится в равновесии.

Рис.1

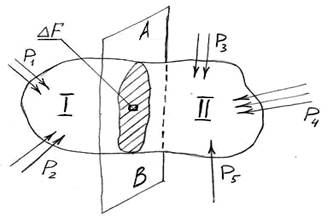
Определим внутренние силовые усилия    в теле, возникающие под действием внешних сил. Для этого проведем в теле плоскость AB. Тело рассекается на две части - I и II. Отбросим одну часть, например, правую. Рассмотрим равновесие левой части (см. рис.2), заменив действие отброшенной части системой сил и моментов, которые являются реакциями отброшенной части.   Если  начало координат установить в центре тяжести поверхности разреза и спроецировать все силы и моменты на оси координат, то  в качестве реакций отброшенной части тела получим внутренние силовые факторы тела:

 – результирующая продольная сила;

– поперечная сила; – поперечная сила;

 – крутящий момент; – изгибающие моменты.

Рис. 2

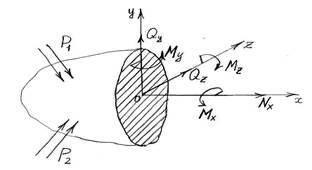
Поскольку тело находится в равновесии, то неизвестные внутренние силовые факторы можно определить через условия равновесия, а именно: сумма проекций на оси координат всех внутренних и внешних сил, действующих на тело, а также сумма моментов относительно осей координат должны равняться нулю. Данные условия равновесия относительно оси х будут следующие.

    ;            .

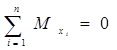Общее количество уравнений равновесия шесть, используя которые можно определить внутренние силы и моменты через известные внешние силы. Такой метод определения внутренних силовых факторов в произвольном сечении называют методом сечений.

Оценим напряженное состояние произвольного сечения, для чего рассмотрим бесконечно малую площадку , расположенную в сечении AB (рис.3).

Рис.3

На бесконечно малую площадку DF на плоскости AB приходится элементарная сила DP, вектор которой имеет некоторый определенный угол наклона   к поверхности. Отношение

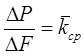
дает вектор средней интенсивности внутренних сил. Переходя к пределу, получим напряжение kв точке О.

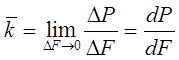    , причем угол наклона  вектора остается неизменным.

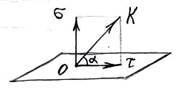
Напряжением kв точке сечения тела называют предел, к которому стремится отношение равнодействующей на площадке внутренней силы DР к величине этой площадки DF при стремлении DF к нулю.

Полное напряжение k можно разложить на две составляющие:

·  составляющую,  нормальную к плоскости сечения, которая называется нормальным напряжением (s). В дальнейшем растягивающему нормальному напряжению будем присваивать знак плюс, а сжимающему – знак минус;

·  составляющую, касательную к плоскости сечения, которая называется касательным напряжением (t).

Для удобства расчетов в дальнейшем изложении t представим в виде двух составляющих по направлению координатных осей Y и Z - t_xy и t_xz  (рис.4).

Рис.4

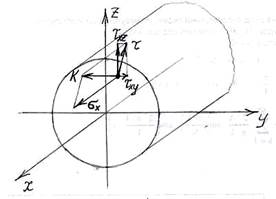
В данном случае в обозначении касательных напряжений имеется два индекса: первый указывает, какой оси параллельна нормаль к площадке действия данного напряжения, а второй – какой оси параллельно само напряжение.

Зная напряженное состояние в любой точке тела (изделия), характеризуемое совокупностью напряжений, можно оценить прочность данного изделия. В простейшем случае оценка прочности производится либо по наибольшему нормальному напряжению, либо по наибольшему касательному напряжению (когда деталь работает на сдвиг). В этом случае условия прочности записываются в виде: