Основы конструирования радиоэлектронных систем. Напряжения: полное, нормальное и касательное, страница 2

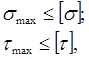
где  ,   - максимально допустимые значения напряжений для данного материала при данных условиях.

Рассмотрим случай осевого растяжения стержня, нагруженного двумя сосредоточенными нагрузками 2Р и 5Р (рис.5 а).

Рассечем стержень плоскостью а-а и отбросим мысленно верхнюю часть стержня, заменив отброшенную часть ее реакцией N₁ (рис.5 б). Условие равновесия для оставшейся части стержня запишется в виде:

N₁+2P-5P=0,

откуда продольная растягивающая стержень сила N₁=3P.

Поступая аналогичным образом с нижней половиной стержня, определяем продольную растягивающую силу N₂. Наглядное представление о законе распределения продольных сил по длине стержня дает график (иначе-эпюра) продольных сил. На эпюре (рис.5 в) по оси ординат в выбранном масштабе откладываются значения продольной силы в поперечном сечении стержня).

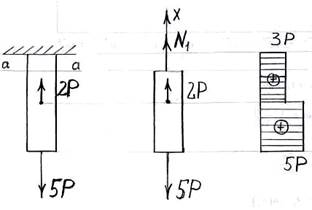
а)                          б)                в)

Рис.5

Продольная сила N есть равнодействующая нормальных напряжений в поперечном сечении.

, где F- площадь поперечного сечения стержня.

При рассмотрении механизмов растяжения-сжатия стержней принимают гипотезу плоских сечений (гипотеза Бернулли), в соответствии с которой поперечные сечения стержня, плоские и нормальные к оси стержня до деформации остаются плоскими и нормальными к оси и после деформации. В связи с этим можно предположить, что нормальные напряжения распределены по поперечному сечению равномерно s = Const. Поскольку s = Const, то , откуда:

.

В простейшем случае, когда действует одна сила P, то  N = P  и

.

Полученные соотношения справедливы и для растяжения, и для сжатия, только сжимающим напряжениям присваивается знак «минус», а растягивающим – знак «плюс».

3. Определение деформаций и перемещений при растяжении-сжатии.

Опытным путем установлено, что в пределах малых деформаций для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональную зависимость между нормальными напряжениями и деформациями:

, где  - относительное удлинение стержня;

 абсолютное удлинение стержня;

- длина стержня до деформации;

E – коэффициент пропорциональности, называемый модулем упругости первого рода (характеризует жесткость материала, то есть определяет его способность сопротивляться деформациям). Величина Е измеряется также, как и , в мегапаскалях (МПа) и определяется экспериментально.

Имея в виду, что: ,  ,  ,  можно определить полное удлинение стержня:

.

Наряду с продольными деформациями существуют и поперечные, т.е. в процессе удлинения сержня под действием нагрузки происходит уменьшение размера его поперечного сечения. Между продольной и поперечной деформациями существует определенная зависимость:

, где ε’ – поперечная деформация, n - коэффициент поперечной деформации (коэффициент Пуассона).

Зная ε’, можно определить полное поперечное сужение или расширение стержня:

, где b – поперечный размер.

В табл.1 даны значения модуля упругости Е для наиболее часто применяемых материалов.

Таблица 1

Значения модулей упругости первого и второго рода и коэффициента Пуассона для различных материалов.

Материал	E, ГПа	G, ГПа	n
Алюминиевая бронза	103	41	0.25
Дюралюминий	70	26	0.31
Медь холоднокатаная	127	48	0.33
Сталь углеродистая	200	8	0.25
Чугун белый	115	44	0.24
Сталь легированная некрист.	206	80	0.25 – 0.3
Бетон	15 – 40	7 – 17	0.33
Гранит	35 – 50	14 – 24	0.1 – 0.15
Каучук	0.008	0.003	0.46
Стекло	50 – 80	0.65	0.39
Корунд	450	200	-
Пробковое дерево	-	-	0

4. Растяжение - сжатие ступенчатого стержня (рис.6).

К концу ступенчатого стержня с площадью поперечного сечения F₁ и F₂ приложена растягивающая нагрузка Р. Требуется определить полную деформацию стержня.

Рис.6

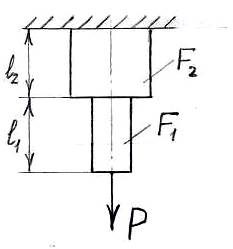
Полное изменение длины ступенчатого стержня определяется как простая сумма деформаций его составных частей, в пределах которых E, N, Fпостоянны.

.

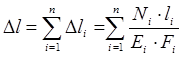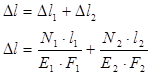
где N₁ = N₂ = P.     

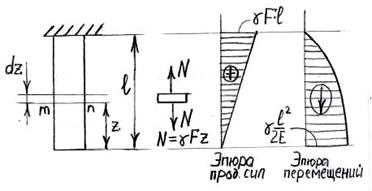
5. Удлинение стержня постоянного сечения под действием силы тяжести (рис.7).

Сила тяжести представляет собой нагрузку, равномерно распределенную по длине стержня.

Обозначим удельный вес материала бруса через g. Рассмотрим деформацию элемента dz на расстоянии z от нижнего конца бруса. Сила растяжения элемента dz будет определяться объемом части бруса длиной z, умноженным на удельный вес g:

.

Рис.7

Удлинение элемента dz равно:

.

Интегрируя это выражение в пределах от z = 0 до z = l, получаем полное удлинение бруса:

.

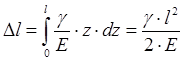Учитывая, что сила тяжести бруса равна ,  то есть , получим:

.

Следовательно, удлинение бруса постоянного сечения от собственной силы тяжести в два раза меньше удлинения от действия силы, равной силе тяжести бруса и приложенной к его концу.