Определение нормальных напряжений в точках поперечного сечения балки, страница 2

Знак "+", поскольку при взгляде на участок DE при движении слева- направо эпюра M_и  восходящая.

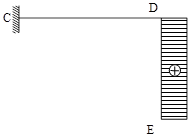
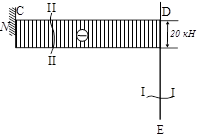
Применяя метод сечений, можно определить продольную силу N. Для стержня DE, проецируя силы, приложенные к стержню ниже сечения I-I на направление от стержня,  получим N=0.

Для стержня  CD,   проецируя силы,  приложенные правее сечения II-II на направление стержня CD, получим N_CD=20 кН .

Строим эпюру продольных сил, причем отрицательные значения продольной силы N откладываем вниз от оси стержня (знак "-" , поскольку стержень подвергается сжатию).

 

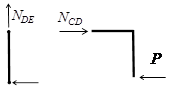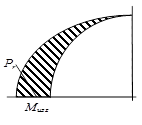
Пример 7. Построить эпюры внутренних силовых факторов пружины, выполненной в виде консольно закрепленного стержня, имеющего форму дуги в четверть окружности радиуса r, нагруженного на свободном конце радиально направленной силой P (рис.45).

 

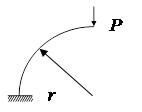Рис.45

Отсечем на угловом расстоянии  от оси O-y часть дуги стержня и составим уравнение равновесия отсеченной части, заменив отброшенную часть стержня ее реакциями R и М_и.

 

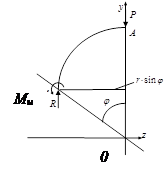Из представленной схемы видно, что равнодействующая внутренних сил R=P, а изгибающий момент найдем из условия, что сумма моментов относительно т.А должна быть равна нулю:  . Будем иметь:

, откуда .

Проецируя равнодействующую внутренних сил R на направление радиуса (дуги) окружности и на касательную к ней, получим значения осевой и поперечной сил:

; (минус поскольку сила сжимающая)

.

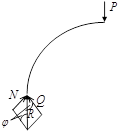
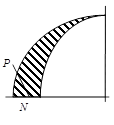
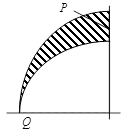
По полученным выражениям изгибающего момента, осевой и поперечной сил строим эпюры, причем отрезки эпюр, соответствующие силам и моментам в сечениях, откладываем по нормали к оси стержня на всей его длине, т.е. в радиальных направлениях.

Пример 8. Построить эпюры внутренних силовых факторов изогнутого в плоскости стержня, нагруженного сосредоточенной силой P, направленной перпендикулярно плоскости расположения стержня (рис.46).

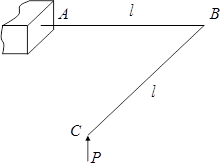
Рис.46

Отсечем мысленно часть стержня на участке BC на расстоянии x от т. C и  составим  уравнение равновесия отсеченной части (сумма моментов относительно произвольно выбранной точки должна быть равна нулю). Из данного уравнения получим значение изгибающего момента для участка ВС:

( знак результата положительный, поскольку выпуклость у балки снизу, т.е. сжатое волокно сверху).

Поперечная сила в сечении определяется как сумма проекций на вертикаль левых от сечения внешних сил, т.е. , причем знак "+", поскольку  эпюра восходящая при движении слева направо.

Теперь можно построить эпюры внутренних силовых факторов для участка ВС.

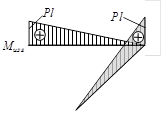
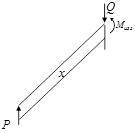
Отсечем теперь часть стержня на участке AB на расстоянии x от точки B и составим схему равновесия отсеченной части:

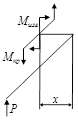
Отсеченная часть стержня находится в равновесии, а в плоскости сечения действуют внутренние силовые факторы: поперечная сила Q, изгибающий момент М_и  и крутящий момент М_кр.

По аналогии с предыдущим определяем изгибающий момент:

, причем знак "+", поскольку выпуклость у балки снизу.

Поперечная сила в сечении определяется как сумма проекций на вертикаль левых от сечения внешних сил:

, причем знак "+", поскольку  эпюра восходящая при движении слева направо.

Величину крутящего момента определим из соответствующего условия равновесия балки относительно оси АВ:

;

При построении эпюр изгибающих и крутящих моментов следует учитывать, что когда стержни рамы пересекаются под прямым углом, то при переходе через прямой угол изгибающий момент превращается в равный ему крутящий момент, если ось последующего участка стержня перпендикулярна плоскости эпюры изгибающего момента предыдущего участка стержня.

12.7. Определение нормальных напряжений в точках поперечного сечения балки.

Нормальное напряжение в любой точке поперечного сечения балки при известном изгибающем моменте при чистом плоском (простом) изгибе определяется из выражения:

, где  - момент инерции сечения относительно нейтральной оси, где y-расстояние от нейтральной оси до рассматриваемого волокна балки.

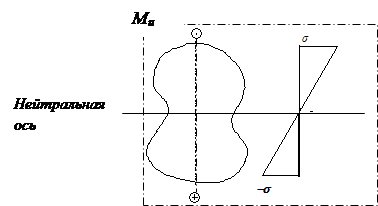
Нейтральной осью называется линия пересечения нейтрального слоя с плоскостью поперечного сечения балки.

Как видно из приведенного примера, нейтральный слой – слой балки не испытывающий при изгибе ни растяжения ни сжатия. При этом верхние слои балки испытывают растяжение (нормальные напряжения максимальны у поверхности стержня и падают до нуля при приближении к нейтральному слою), а нижние слои – испытывают сжатие.

 

Если же изгиб поперечный, то  в поперечных сечениях балки возникают и нормальные, и касательные напряжения. Возникают деформации сдвига, в результате чего поперечные сечения перестают быть плоскими. Однако приведенная формула дает вполне надежные результаты и при поперечном изгибе.