Петербургский Государственный Университет
Путей Сообщения
Kaфeдpa “Элeктpичecкaя тяга”
Лабораторная работа № 1
ВЛИЯНИЕ РЕССОРНОГО ПОДВЕШИВАНИЯ НА ВЕРТИКАЛЬНУЮ ДИНАМИКУ ЭКИПАЖА
Выполнил студен
Группы ЭТ-502
Рабинюк А.А.
CAHKT-ПETEPБУPГ
2008
Цель работы - определение силы динамического вертикального воздействия одноосного экипажа при движении с различными скоростями по рельсовому пути с периодически повторяющимися неровностями.
Экипаж без рессорного подвешивания.
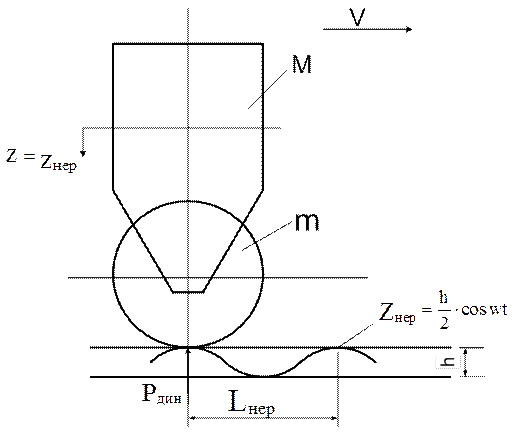
Рис.1
Уравнение вертикальной динамики (см.рис.1) в этом случае имеет вид:
![]()
![]()
![]()
или![]()
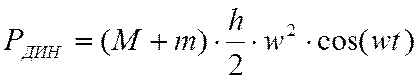 ,
,
где 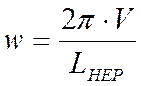 .
.
Отсюда:
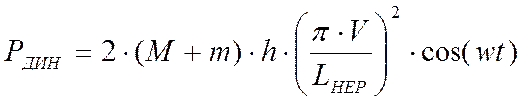 , (кН)
, (кН)
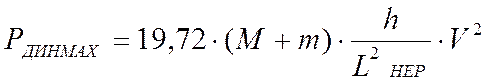 , (кН).
, (кН).
где M+m – масса экипажа в т, отнесённая к одной оси;
h – глубина неровности, м;
Lнер - длина неровности, м;
V – скорость движения экипажа, м/с;
Экипаж с рессорным подвешиванием.
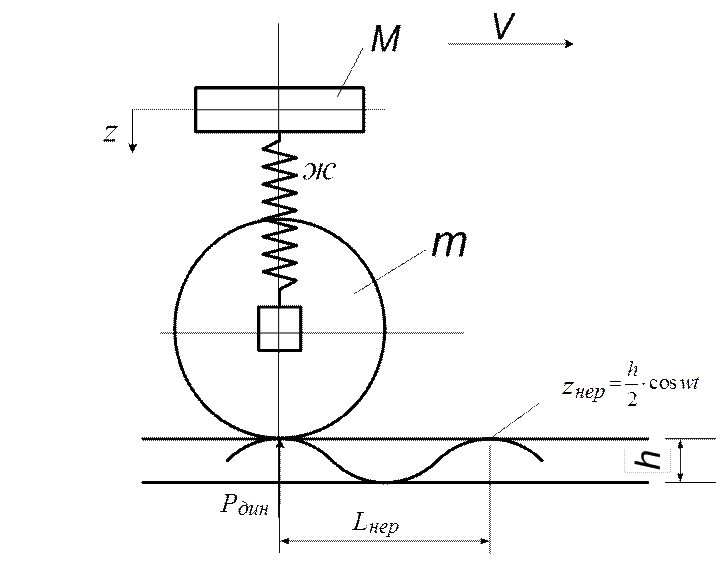
Рис.2.
Пусть есть упругий элемент (рессора) между массой M (подрессоренные части) и m (масса неподрессоренных частей) (рис.2.).
Пусть: ж – жесткость рессорного подвешивания, отнесённая к одной оси, кН/м;
z – текущая координата вертикальных перемещений центра тяжести подрессоренной массы M;
zнер – текущая координата неровности пути.
Уравнение вертикальных колебаний:
|
M· |
(1) |
|
m· |
(2) |
Решение уравнения (1) ищем в виде:
z=A·cos(wt)
После подстановки данного выражения в уравнение (1) получаем:
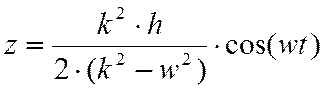 ,
,
где
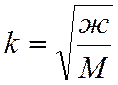 ,1/с – круговая частота свободных
колебаний;
,1/с – круговая частота свободных
колебаний;
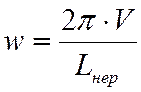 ,1/с – круговая частота вынужденных
колебаний.
,1/с – круговая частота вынужденных
колебаний.
Если w→k, то амплитуда колебаний A=zmax→∞,то есть имеет место резонанс колебаний. Соответствующая скорость движения называется резонансной или критической.
Тогда k=w или
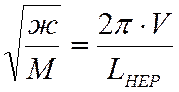 .
.
Отсюда:
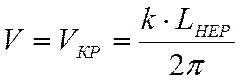 , м/с
, м/с
или
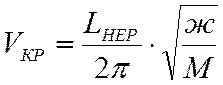 , м/с
, м/с
![]()
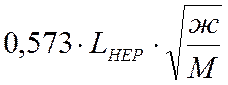 ,
км/ч.
,
км/ч.
После подстановки найденного решения в уравнение (2) получим:
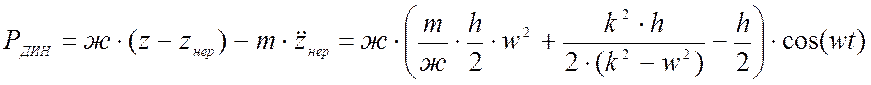
Отсюда максимальное значение ![]() :
:
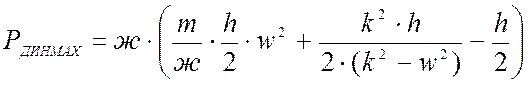 , кН.
, кН.
Экипаж с гасителем колебаний в системе одноярусного рессорного подвешивания.
Уравнение вертикальной динамики (см. рис.3) в случае колебаний экипажа с гасителем колебаний в системе одноярусного рессорного подвешивания имеет вид:
|
|
(3) |
|
|
(4) |
Коэффициент сопротивления гидравлического гасителя колебаний:
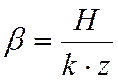 кНс/м ,
кНс/м ,
где 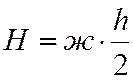 - максимальное значение возмущающей
силы, кН;
- максимальное значение возмущающей
силы, кН;
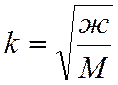 -
частота свободных колебаний,1/с;
-
частота свободных колебаний,1/с;
![]() - амплитуда вертикальных колебаний
подрессоренной массы М, м;
- амплитуда вертикальных колебаний
подрессоренной массы М, м;
![]() - коэффициент вертикальной динамики
по амплитуде (см. Бирюков “Механическая часть подвижного состава”);
- коэффициент вертикальной динамики
по амплитуде (см. Бирюков “Механическая часть подвижного состава”);
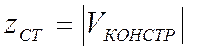 - статический прогиб рессорного
подвешивания, м.
- статический прогиб рессорного
подвешивания, м.
Отсюда:
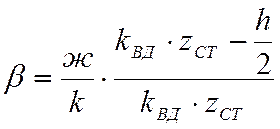 ,
, 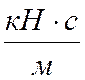
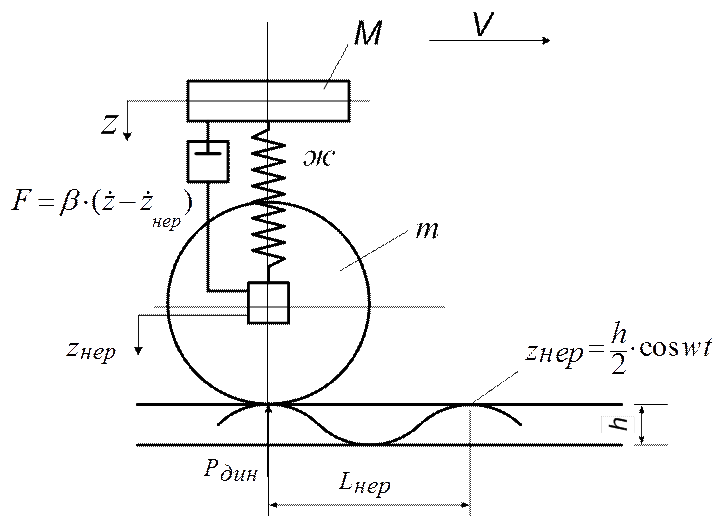
Рис.3
Из уравнения (4):
![]() .
.
После подстановки и некоторых преобразований получим:
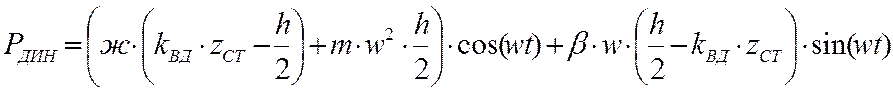
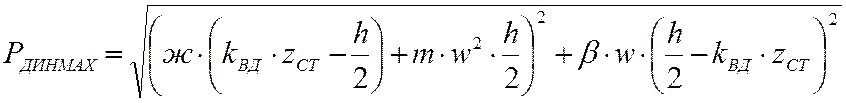 ,
кН.
,
кН.
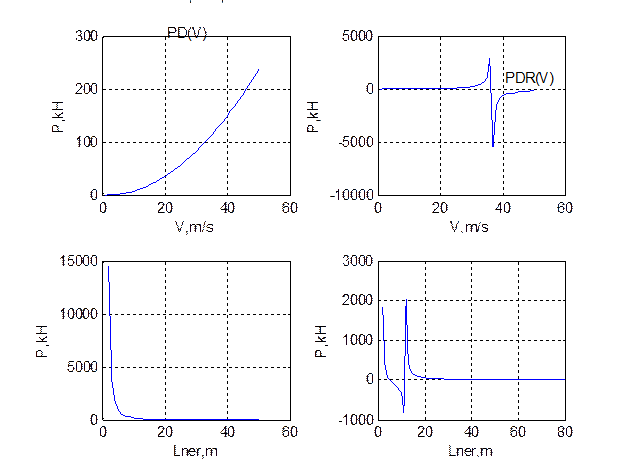
M=22.5; MK=3.5; hner=0.03; Vmax=110; Vmax=Vmax/3.6; Lner=12.5;
G=M*1000*9.81/Vmax;
K=sqrt(G/M);
%Расчет Рдин(V) дл экипажа с безрессорным подвешиванием
V=0;
for I=1:50
PD(I)=(M+MK).*hner/2.*(2.*pi.*V/Lner).^2;
V=V+1;
end;
V=1:1:50;
subplot(2,2,1),plot(V,PD);
grid
xlabel('V,m/s');
ylabel('P,kH');
text(21,305,'PD(V)');
%Расчет Рдин(V) дл экипажа с рессорным подвешиванием
V=0;
for I=1:50
W=(2.*pi.*V)./Lner;
PDR(I)=G.*hner./2.*(K.*K./(K.*K-W.*W)-1+MK./G.*(W.*W));
V=V+1;
end
V=1:1:50;
subplot(2,2,2),plot(V,PDR);
grid
xlabel('V,m/s');
ylabel('P,kH');
text(41,1010,'PDR(V)');
%Расчет Рдин(Lнер) дл экипажа с безрессорным подвешиванием
V=Vmax;
Lner=0;
for I=1:50
PD(I)=(M+MK).*hner/2.*(2.*pi.*V/Lner).^2;
Lner=Lner+1;
end;
Lner=1:1:50;
subplot(2,2,3),plot(Lner,PD);
grid
xlabel('Lner,m');
ylabel('P,kH');
text(21,40010,'PD(Lner)');
%Расчет Рдин(Lнер) дл экипажа с рессорным подвешиванием
Lner=0;
V=Vmax;
for I=1:80
W=(2.*pi.*V)./Lner;
PDR(I)=G.*hner./2.*(K.*K./(K.*K-W.*W)-1+MK./G.*(W.*W));
Lner=Lner+1;
end
Lner=1:1:80;
subplot(2,2,4),plot(Lner,PDR);
grid
xlabel('Lner,m');
ylabel('P,kH');
text(30,10010,'PDR(Lner)');
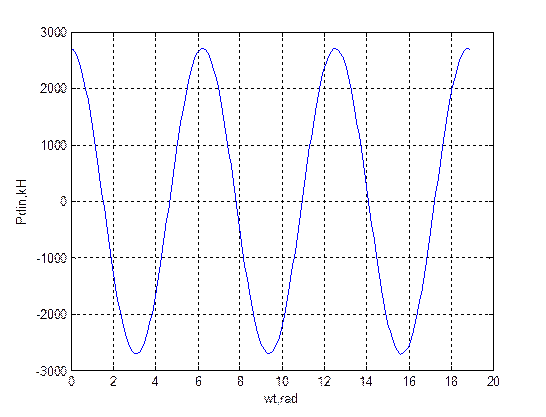
M=22.5;
h=0.03;
Vmax=110;
Lnep=12.5;
zst=Vmax*0.01;
Kvd=0.34; %Коэффициент вертикальной динамики
V=Vmax/3.6;
G=M*1000*9.81/V
k=sqrt(G/M)
Vkr=k*(Lnep/(2*pi))
w=2*pi*Vkr/Lnep
beta=G/k*((Kvd*zst-h/2)/(Kvd*zst))
t=0:pi/32:pi*6;
Pgin=(G*(Kvd*zst-h/2)+M*w*w*h/2)*cos(t)+beta*(h/2-Kvd*zst)*sin(t)
plot(t,Pgin);
grid;
xlabel('wt,rad');
ylabel('Pdin,kH');
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.