Машиностроение \ Динамика вагонов

Определение угла наклона кузова и скорости начала опрокидывания экипажа при движении в кривой, и влияние на их величины основных параметров экипажа и пути

Страницы работы

8 страниц (Word-файл)
Посмотреть все страницы
Скачать файл

Содержание работы

Петербургский Государственный Университет Путей Сообщения

Kaфeдрa “Элeктpичecкaя тяга”

Лабораторная Работа № 2

ОПРЕДЕЛЕНИЕ СКОРОСТИ НАЧАЛА ОПРОКИДЫВАНИЯ ЭКИПАЖА ПРИ ДВИЖЕНИИ В КРИВОЙ

Выполнил студент

                                                                                           Группы ЭТ-502

                                                                                         Рабинюк А.А.

CAHKT-ПETEPБУPГ

2008


Цель работы - определение угла наклона кузова и скорости начала опрокидывания экипажа при движении в кривой, и влияние на их величины основных параметров экипажа и пути.

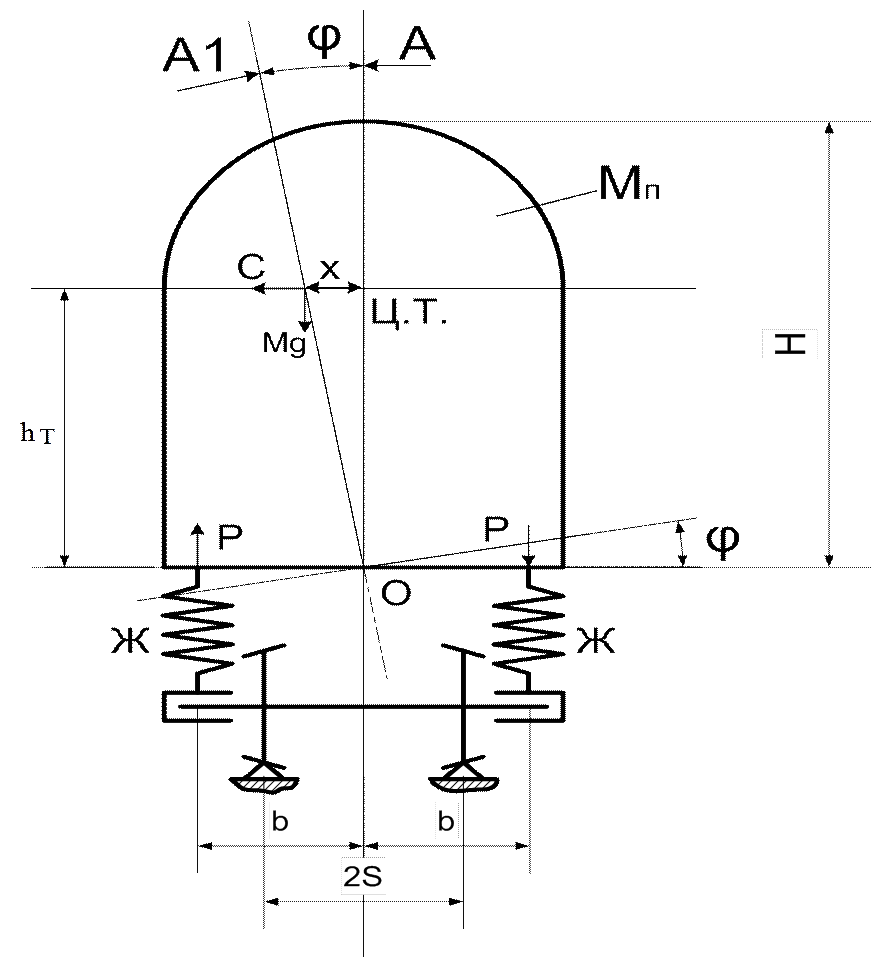
Рис. 1.

Расчётная схема экипажа и действующих на него сил представлена на рис. 1.

На рис.1:

 – подрессоренная масса экипажа, т:

,

где - подрессоренная масса экипажа, отнесенная к одной оси, т;

- число осей экипажа;

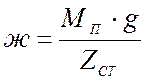 - жёсткость одной стороны рессорного подвешивания экипажа, кН/м;

 - статический прогиб рессорного подвешивания, м;

 - высота центра тяжести надрессорного строения от верхней плоскости рессорного подвешивания, м;

 - угол наклона надрессорного строения, рад;

 - расстояние между осями рессорных комплектов в поперечной плоскости, м.

При расчётах принять  м;

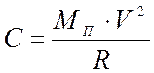 - центробежная сила инерции, возникшая при движении экипажа по кривой, кН;

P – реакции рессорного подвешивания, вызванные наклоном надрессорного строения на угол .

Из приведённой на рис.1 схемы следует, что при движении в кривой на подрессоренную часть действует опрокидывающий момент:

, кН·м,

где .

Этому моменту противодействует восстанавливающий момент реакций рессорного подвешивания:

, кН·м.

Здесь:

, кН,

тогда:

, кН·м.

.

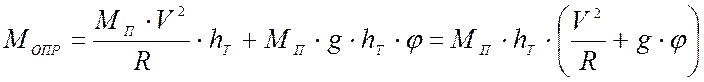Условием равновесия надрессорного строения является равенство:

,

или

.

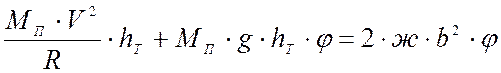Преобразуя выражение, получим:

.

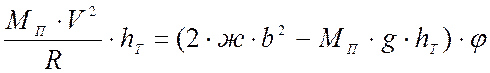Отсюда:

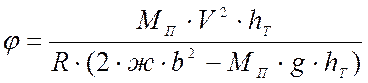, рад.

Очевидно, устойчивость экипажа против опрокидывания будет обеспечена при условии:

<<,

где  - максимально допустимый угол наклона надрессорного строения, рад.

Условиям, при которых опрокидывание экипажа станет неизбежным, соответствует равенство x= b, т.е. когда:

,

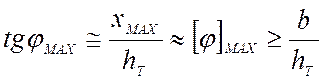так при  м и  м;  рад.

При этом реакции рессор достигнут величины:

, кН

и

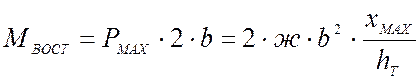, кН·м.

Из равенства (в этих условиях):

Находим:

,

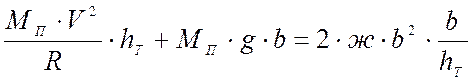что даёт возможность определить скорость начала опрокидывания экипажа:

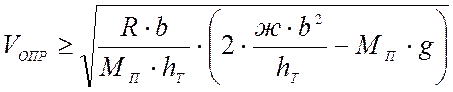, м/с

- без учёта возвышения наружного рельса (h=0),

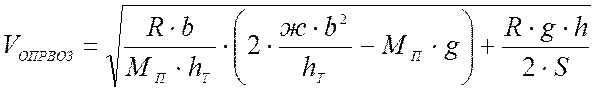, м/с

- с учётом возвышения наружного рельса (h≠0).

2S=1,6 – расстояние между кругами катания колёс, м.

Отклонение любой точки А от её среднего положения определяется из выражения:

,

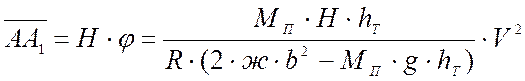где  H – высота точки А над верхней плоскостью рессорного подвешивания, м.


Программа работы

  1. Построить графические зависимости: V=f(R) при наличии возвышения внешнего рельса (h=var), и при отсутствии возвышения внешнего рельса (h=0).
  2. Построить графические зависимости V=f(R) при изменении величины статического прогиба рессорного подвешивания .
  3. Построить графические зависимости V=f(R) для разных значений высоты центра тяжести надрессорного строения от верхней плоскости рессорного подвешивания .
  4. Определить угол наклона надрессорного строения .
  5. Определить максимально допустимый угол наклона надрессорного строения .
  6. Определить отклонение точки А от её среднего положения.
  7. Определить скорость начала опрокидывания экипажа  без учёта возвышения наружного рельса (h=0) и  с учётом возвышения наружного рельса (h≠0).

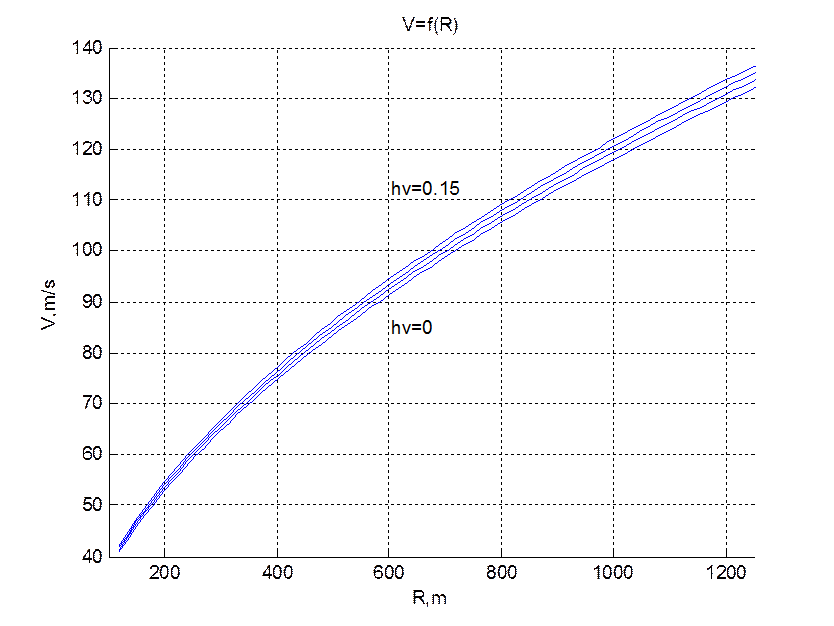
Рис.2 Зависимость V=f(R) при изменении параметра h

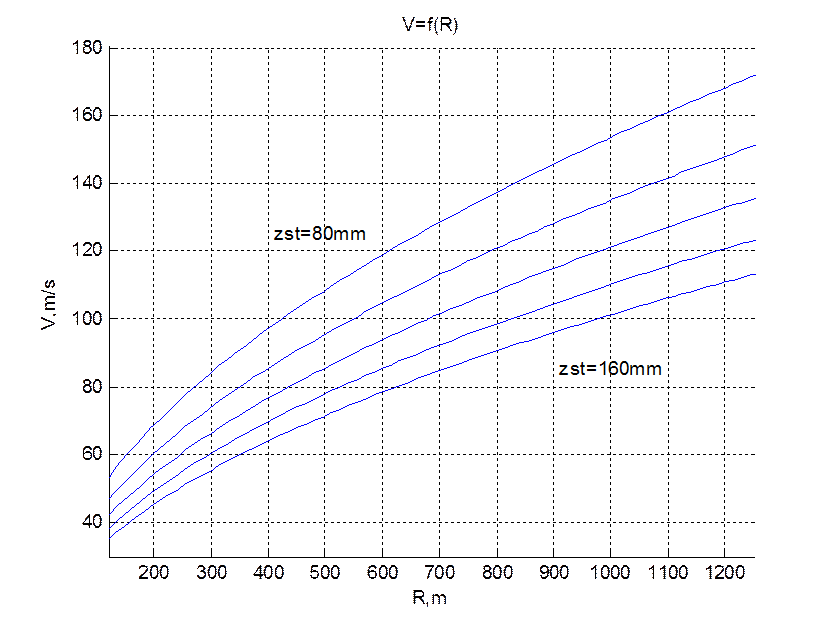
Рис.3 Зависимость V=f(R) при изменении параметра

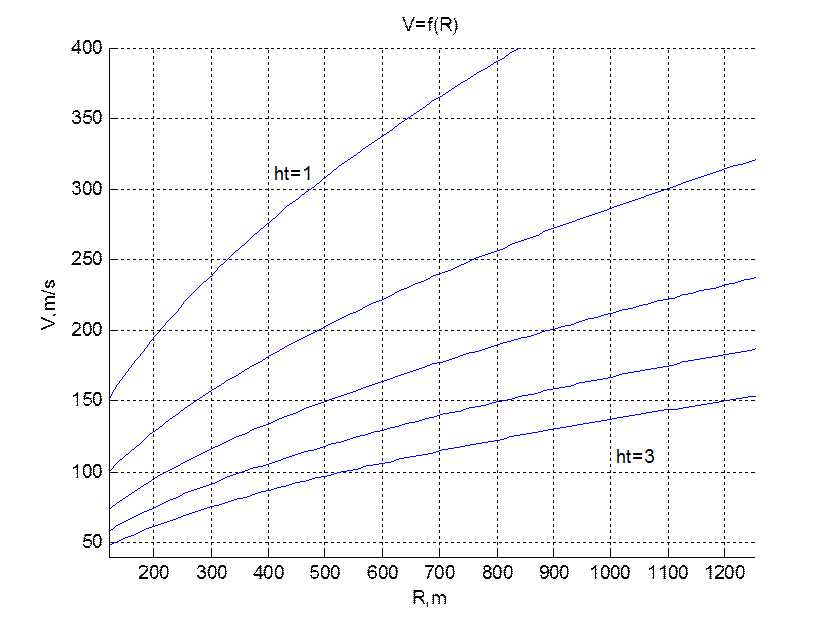
Рис.4 Зависимость V=f(R) при изменении параметра


Программа

V=110/3.6;

g=9.81;

S1=0.79;

hv=0.1;

b=1.4;

ht=3.5;

ht0=ht;

R=200;

R0=R;

M=22.5;

n=2;

M=M*n;

zst=0.13;

zst0=zst;

H=6;

phi=M*V^2*ht/(R*(2*M*g/zst*b^2-M*g*ht))

phimax=b/ht

AA1=H*phi

Voprvoz=sqrt(R*b/(ht*M)*(2*M*g/zst*b^2/ht-M*g)+R*g*hv/(2*S1))

Vopr=sqrt(R*b/(ht*M)*(2*M*g/zst*b^2/ht-M*g))

axis([100 1250 40 140]);

hold on;

for I=1:4;

    R=120:15:1260;

    plot(R,sqrt(R*b/(ht*M)*(2*M*g/zst*b^2/ht-M*g)+R*g*hv/(2*S1)));

    hv=hv+0.05;

end;

grid

ylabel('V,m/s');

xlabel('R,m');

title('V=f(R)');

text(605,85,'hv=0');

text(605,112,'hv=0.15');

pause

hold off;

clg;

axis([120 1250 30 180]);

hold on;

hv=0;

zst=0.08;

for I=1:5;

    R=120:15:1260;

    plot(R,sqrt(R*b/(ht*M)*(2*M*g/zst*b^2/ht-M*g)+R*g*hv/(2*S1)));

    zst=zst+0.02;

end;

grid

ylabel('V,m/s');

xlabel('R,m');

title('V=f(R)');

text(410,125,'zst=80mm');

text(910,85,'zst=160mm');

pause

hold off;

clg;

axis([120 1250 40 400]);

hold on;

ht=1;

zst=zst0;

for I=1:5;

    R=120:15:1260;

    plot(R,sqrt(R*b/(ht*M)*(2*M*g/zst*b^2/ht-M*g)+R*g*hv/(2*S1)));

    ht=ht+0.5;

end;

grid

ylabel('V,m/s');

xlabel('R,m');

title('V=f(R)');

text(410,310,'ht=1');

text(1010,110,'ht=3');

pause

hold off;

clg;

ht=ht0

phi = 0.1102

phimax = 0.3143

AA1 = 0.6611

Voprvoz = 52.7939

Vopr = 51.6045

Похожие материалы

Информация о работе

ВУЗ:
Петербургский государственный университет путей сообщения (ПГУПС)
Предмет:
Динамика вагонов
Тип:
Отчеты по лабораторным работам
Категория:
Машиностроение (Технические предметы)
Размер файла:
179 Kb
Скачали:
0
Скачать файл