Вынужденные колебания одноосного вагона с учетом упругости пути.
Математическая модель и её решение
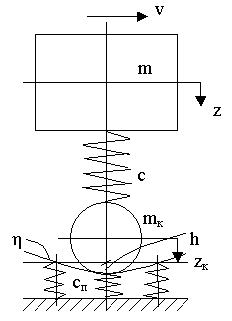
Для выбора расчетной схемы примем следующие допущения.
Части вагона обладают только свойствами инерции, упругими свойствами не обладают.
Рессорное подвешивание обладает только упругими свойствами, свойствами инерции и трения не обладает.
Путь обладает упругими свойствами и приведенной массой, свойствами трения не обладает.
 Уравнения движения:
Уравнения движения:
![]()
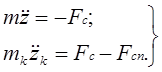 , (1)
, (1)
где 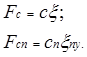
![]()
Деформации подвешивания, рельсового пути и смещение колесной пары соответственно равны
![]() .
.
С учетом этих зависимостей уравнения движения примут вид:
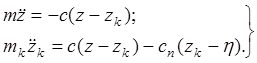 (2)
(2)
Раскроем скобки и перенесем все
Рис.1. Расчетная схема неизвестные силы влево. В итоге получим:
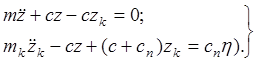 (3)
(3)
Представим зависимость ординаты траектории точки контакта колеса и рельса относительно оси неровности выражением:
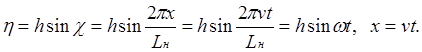
Преобразуем систему (3) – разделим каждое уравнение на коэффициент при старшей производной и введем обозначения:
![]()
В результате получим систему уравнений в следующем виде:
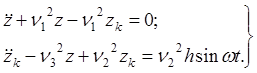 (4)
(4)
Частное решение этой системы будем искать в виде гармонических функций, сходных с правой частью системы (4):
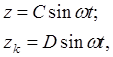 (5)
(5)
где C, D, -неизвестные постоянные величины, подлежащие определению.
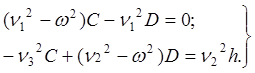 (6)
(6)
В итоге получена алгебраическая система (6) двух неоднородных уравнений, с двумя неизвестными. Выпишем и раскроем её определитель
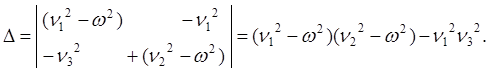 (7)
(7)
Известно, что определитель
(7) равен нулю при условии, что ![]() и
и ![]() (из этого условия находятся
собственные частоты
(из этого условия находятся
собственные частоты ![]() ).
).
Выпишем решение системы (6), используя формулы Крамера:
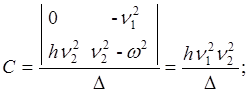
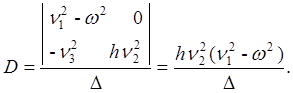
Теперь можно записать частное решение системы (6):
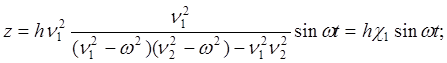
(8)
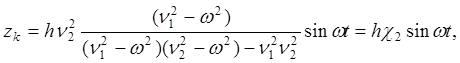
где ![]() –коэффициенты
динамичности кузова и неподрессоренных частей, соответственно.
–коэффициенты
динамичности кузова и неподрессоренных частей, соответственно.
При изучении движения системы в течение длительного времени свободные колебания, как затухающие, интереса не представляют. Движение кузова будет, полностью определятся выражениями (8).
1) При малых ![]() , скорость движения мала, кузов и
неподрессоренные части повторяют траекторию рельсовой неровности без деформации
упругих связей.
, скорость движения мала, кузов и
неподрессоренные части повторяют траекторию рельсовой неровности без деформации
упругих связей.
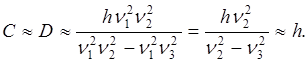
2) ![]() будут значительно
возрастать при
будут значительно
возрастать при ![]() (при этих условиях
(при этих условиях ![]() ), то есть проявляются два
резонансных режима на двух критических скоростях.
), то есть проявляются два
резонансных режима на двух критических скоростях.
3) Отношения координат ![]() при
при ![]() равно
равно
![]() , то есть соответствует собственным
(главным) формам колебаний (см. Свободные колебания одноосного вагона с учетом упругости пути).
, то есть соответствует собственным
(главным) формам колебаний (см. Свободные колебания одноосного вагона с учетом упругости пути).
4) При ![]() ,
,
![]()
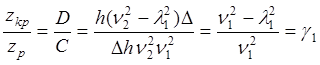 –
первая собственная форма.
–
первая собственная форма.
При ![]() ,
,
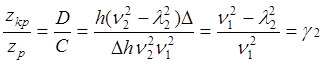 – вторая собственная форма.
– вторая собственная форма.
Выражения, определяющие
координаты частей вагона при первом резонансе (![]() ),
имеют вид
),
имеют вид
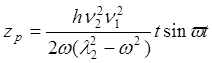 ,
, 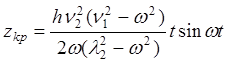
Грофическое представление
изменений коэффициентов динамичности ![]() в зависимости от
изменений
в зависимости от
изменений ![]() имеет вид представленный на рис.2.
имеет вид представленный на рис.2.
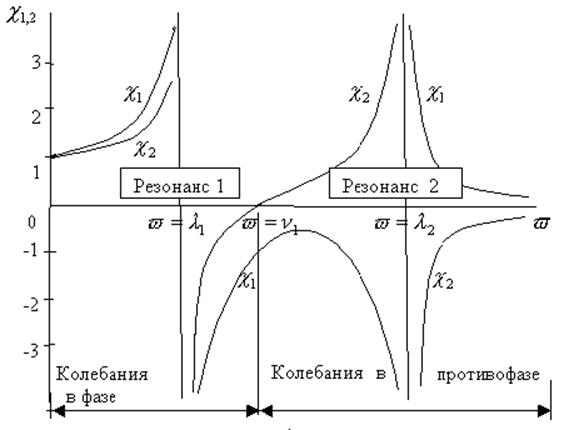
Рис. 2. Зависимости величин
коэффициентов динамичности от изменений ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.