Поиск минимальных разбиении. Приближенные методы

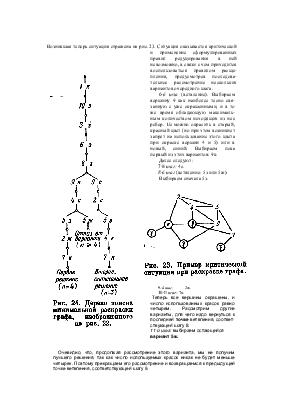
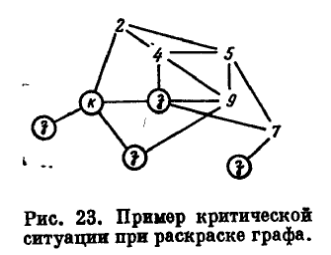
Возникшая теперь ситуация отражена на рис. 23. Ситуация оказывается критической и применение сформулированных правил редуцирования в ней невозможно, в связи с чем приходится воспользоваться правилом расщепления, предусмотрев последовательное рассмотрение нескольких вариантов очередного шага.

6-й шла (ветвление). Выбираем вершину 9 как наиболее тесно связанную с уже окрашенными, и в то же время обладающую максимальным количеством исходящих из нее ребер. Ее можно окрасить в старый, красный цвет (но при этом возникнет запрет на использование этого цвета при окраске вершин 4 и 5) или в новый, синий. Выбираем пока первый из этих вариантов: 9к.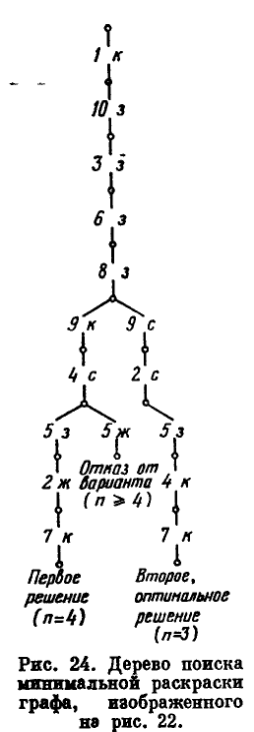

Далее следуют:

7-й шаг: 4с.

8-й шаг (ветвление: 5з или 5ж).

 Выбираем сначала 5з.

9-й шаг:           2ж.

10-й шаг: 7к.

Теперь все вершины окрашены, и число использованных красок равно четырем. Рассмотрим другие варианты, для чего надо вернуться к последней точке ветвления, соответствующей шагу 8.

11-й шаг: выбираем остающийся вариант 5ж.

Очевидно, что, продолжая рассмотрение этого варианта, мы не получим лучшего решения, так как число используемых красок никак не будет меньше четырех. Поэтому прекращаем его рассмотрение и возвращаемся к предыдущей точке ветвления, соответствующей шагу 6.

12-й шаг: выбираем оставшийся вариант 9с.

18-й шаг: 2с.

14-й шаг: 5з.

15-й шаг: 4к.

16-й шаг: 7к.

На этом процесс окраски вершин завершается. Минимальность числа использованных красок — в данном случае трех — гарантируется описанным методом, реализующим достаточный для этого перебор вариантов. Полученное решение совпадает с решением, изображенным на рис. 22, б.

Процесс решения, описанный нами во всех подробностях, можно представить более компактно деревом поиска, показанным на рис. 24.

Метод конденсации. Итак, мы познакомились с таким методом последовательной раскраски вершин графа, при котором очередной вершине назначается вполне определенный цвет, сменить который можно только при возврате к соответствующей точке ветвления в дереве поиска. Между тем возможен и другой подход, при котором перекраска вершин становится типичной. Этот подход порождает новый способ решения задач, связанных с поиском минимальных разбиений множеств. Назовем его методом, конденсации (почему именно так, будет показано ниже) и проиллюстрируем на примере формулируемой сейчас задачи о минимальной имплицирующей матрице.

Для начала введем некоторые определения. Рассматривая троичный вектор и, обозначим через No (u) множество номеров тех его компонент, которые обладают значением 0. Аналогично введем множества N1 (u) и N_ (u). Будем говорить, что троичный вектор u имплицирует троичный вектор v, если No (v) Í Nо (u) и N1(v) Í N1(u) (это название отношения оправдывается тем, что при интерпретации троичных векторов как элементарных конъюнкций оказывается, что последние действительно находятся в отношении импликации).

Положим далее, что матрица U имплицирует матрицу V, если для каждой строки матрицы V найдется имплицирующая ее строка в матрице U и для каждой строки матрицы U найдется имплицируемая ею строка в матрице V.

Очевидно, что для заданной матрицы V можно найти много различных имплицирующих ее матриц. Наша задача заключается в том, чтобы найти минимальную среди них (по числу строк).

Нетрудно сообразить, что сформулированная задача эквивалентна задаче разбиения множества строк матрицы V на минимальное число таких классов, каждый из которых будет образован взаимно неортогональными строками — будем считать такие строки совместимыми. Построив так называемый граф несовместимости, вершины которого соответствуют строкам матрицы V, а ребра указывают на пары, находящиеся в отношении ортогональности, мы увидим, что решение рассматриваемой задачи сводится к нахождению минимальной раскраски этого графа.

Следовательно, задачу можно решить уже знакомим нам способом, например путем образования всех максимальных подмножеств взаимно совместимых строк матрицы V (максимальных пустых подграфов), построения соответствующей булевой матрицы отношения принадлежности строк этим подмножествам и нахождения её кратчайшего покрытия. Однако более практичным при решении этой задачи окажется именно метод конденсации.

Идея метода заключается в образовании множества так называемых капель, составленных из взаимно совместимых строк, и последовательном преобразовании этого множества путем попарного слияния некоторых капель.. Этот процесс, условно называемый конденсацией, начинается с исходной ситуации, когда каждая строка матрицы образует свою, отдельную, каплю, и завершается некоторой  тупиковой ситуацией, когда уже никакая пара капель не может быть слита в одну: оказывается, что каждая пара капель содержит некоторую пару ортогональных строк, одна из которых принадлежит первой капле, другая — второй.

Пусть некоторая капля образована элементами подмножества R = {г1,r2, ...,rq} множества всех строк матрицы V.                                       

Отождествим ее с вектором г, для которого  N0(г) = N0(r1) U No (r2) U • • • U No (rq), N1(r) = N1 (r1) U N1 (r2) U • • • U N1 (rq).