Поиск минимальных разбиении. Приближенные методы, страница 4

Разнообразие стратегий поиска увеличивается, если стоимость искомых решений можно как-то оценить еще до их получения или в процессе их «построения». Допустим, что это можно сделать в каждой из ситуаций, представляемых вершинами дерева поиска, определив на ней значение оценки стоимости, задающей нижнюю границу стоимости решений, получаемых исходя из этой ситуации. Например, при поиске кратчайшего столбцового покрытия булевой матрицы, когда решения конструировались путем наращивания некоторых подмножеств столбцов при движении по дереву поиска сверху вниз, мы пользовались простейшей оценкой стоимости решений, вытекающих из рассматриваемой ситуации. Она принималась равной числу столбцов, уже включенных в соответствующее подмножество.

Пользуясь оценкой стоимости, можно сокращать дерево поиска, запоминая лучшее из уже найденных решений и отказываясь затем от расщепления ситуаций, на которых оценка стоимости принимает значение, большее или равное стоимости этого решения. Эта идея может быть реализована и в рамках метода обхода дерева поиска, как это было сделано при описании способа решения задачи о кратчайшем покрытии, и в рамках метода поярусного построения дерева. При этом вершины дерева поиска будут рассматриваться в порядке, предписанном этими методами, но некоторые из них будут отсекаться. Рассмотрение очередной вершины заключается в выяснении того, не представляет ли она решение, в вычислении значения оценки стоимости в противном случае, и в расщеплении ситуации, если эта оценка ниже стоимости лучшего из уже найденных решений.

На рис. 28 показан уже знакомый нам пример полного дерева поиска, на вершинах которого на этот раз заданы значения оценки стоимости (допустим, что они именно такие). Результаты усечений этого дерева по

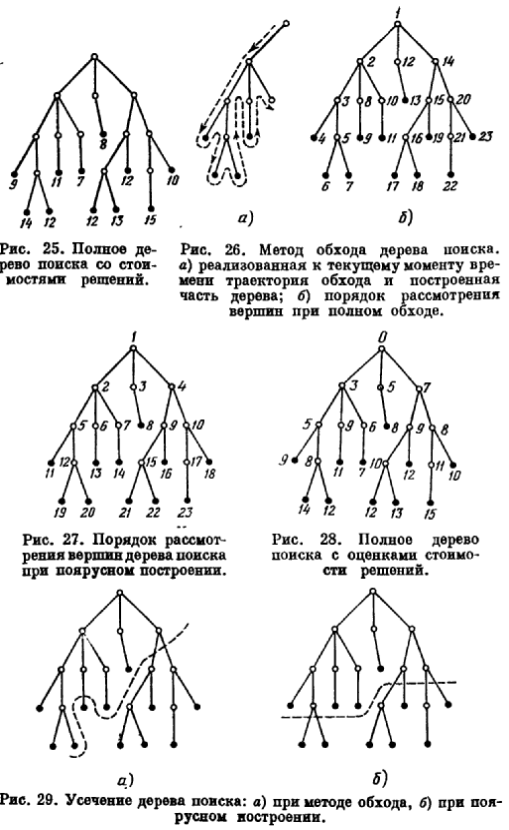
                                рассмотренным методам представлены на рис. 29 (отсекаемые вершины отделены штриховой линией).

На использовании оценок стоимости основан и широко известный метод ветвей и границ, суть которого заключается в таком порядке расщепления вершин, при котором каждый раз среди концевых вершин участка дерева поиска, построенного к текущему моменту времени, выбирается вершина с минимальным значением оценки стоимости. При ее последующем расщеплении сразу же подсчитываются значения оценки стоимости для вершин — продуктов расщепления. Метод ветвей и границ хорош тем, что при нем увеличивается вероятность того, что уже первые из находимых решений будут близки к оптимальным. Это увеличивает число вершин, выбрасываемых из последующего рассмотрения (как это видно на рис. 30, где проиллюстрировано решение данным методом старого примера).

Иногда, например, в задаче о кратчайшем покрытии, стоимость решения равна длине пути, связывающего корень дерева с вершиной, представляющей решение. При этом простейшей оценкой стоимости решений, порождаемых некоторой ситуацией, может служить номер яруса, на котором расположена соответствующая данной ситуации вершина. В этом случае метод ветвей и границ практически совпадет с методом поярусного построения дерева.

Наряду с отмеченным достоинством метод ветвей и границ обладает и существенным недостатком, затрудняющим его, применение. Этим недостатком являются повышенные требования к памяти, необходимой для фиксирования информации о всех концевых вершинах построенного участка дерева, т. е. о соответствующих им ситуациях, ожидающих своего расщепления. При решении многих практически интересных задач число таких ситуаций может достигать весьма больших значений.

Заметим, что этим же недостатком обладает и метод поярусного построения дерева.

Более практичным в подобных случаях оказывается метод обхода дерева поиска, реализующий так называемый лексикографический перебор вариантов, порождаемых последовательным расщеплением ситуаций: продукты расщепления каждой ситуации нумеруются и перебираются: затем в соответствующем порядке. При методе обхода достаточно сохранять в памяти информацию лишь о тех ситуациях, которые соответствуют вершинам, расположенным на пути от рассматриваемой вершины к корню дерева. Объем этой информации, как правило, невелик.