Согласно построению вектор г имплицирует все элементы множества R, играя при этом роль простой импликанты. Последнее означает, что любое сокращение множества No(r) или множества N1(r), т. е. замена в векторе r любой единицы или нуля значением «—», приводит к тому, что этот вектор перестает быть импликатной по крайней мере для одного из элементов множества R.
Таким образом, операция слияния взаимно неортогональных векторов r1,r2,…,rq определяется строго формально как операция нахождения их общей простой пмпликанты r. Введем для этой операции специальное обозначение:
r=r1* r2 * . . . * rq.
Из определений следует, что две различные капли r u s могут слиться тогда и только тогда, когда векторы r и s совместимы, т. е. взаимно неортогональны:
N0(r) Ç N1(s) = Æ и N1(r) Ç Nо(s) =Æ.
Если слияние возможно, то получаемая в результате этого действия капля будет описываться вектором r*s.
Любая текущая ситуация тождественна некоторому множеству капель и, следовательно, может быть представлена некоторой троичной матрицей Т (строки — капли), аналогично тому, как описывается и исходная ситуация Т0= =V. Процесс решения задачи в целом отображается некоторой ветвящейся последовательностью значений матрицы Т, приводящей к тупиковым ситуациям, среди которых находится искомое решение — минимальная имплицирующая матрица для матрицы V.
Из общих соображений следует, что слияние двух строк ti иtj не ухудшит ситуацию, если получаемая в результате строка tk = ti * tj будет обладать не меньшими возможностями слияния с другими строками, чем строка ti, или чем строка tj. Обозначив через T’i и Т’j подмножества строк переменной матрицы Т, совместимых соответственно со строками ti и tj, и учитывая, что T’k = Т’iÇ Т'j, сформулируем следующее правило редуцирования.
Правило слияния строк. Совместимые строки ti и tj сливаются, если выполняется по крайней мере одно из условий: T'iÍ T'j или T’jÍ T'i.
В частности, эти условия всегда выполняются, если одна из рассматриваемых строк имплицирует другую. Этот случай особенно интересен, поскольку нахождение такихпар строк достаточно просто. С другим простым случаем мы встречаемся, когда строка ti совместима со строкой tj и только с ней.
Матрица Т может редуцироваться также путем уменьшения числа ее столбцов, для чего применяется следующее правило.
Правило удаления столбца. Если в некотором столбце матрицы Т отсутствует значение 0 (или 1), то принимается решение поставить в соответствующем столбце искомой матрицы-импликанты всюду инверсное значение 1 (или 0), после чего данный столбец игнорируется, т. е. удаляется из матрицы Т. Столбец удаляется и в том случае, когда он состоит целиком из символов «—». Это значение присваивается всем компонентам соответствующего столбца матрицы-импликанты.
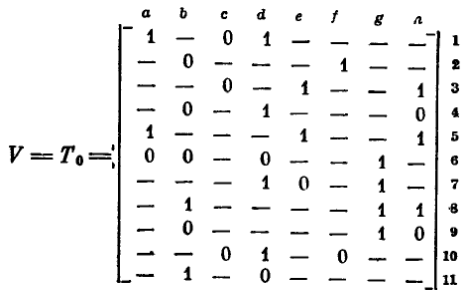 |
Прежде всего удалим столбцы с и g, запомнив, что в результативной матрице-импликанте они должны будут получить, соответственно значения 0 и 1. После этого оказывается, что строка 3 имплицируется строкой 5, и, следовательно, ее также можно удалить, поскольку продукт слияния этих строк совпадает со строкой 5. В аналогичном отношении оказываются строки 9 и 4, и строка 9 так же удаляется. Трансформированная таким образом матрица Т принимает следующее значение:
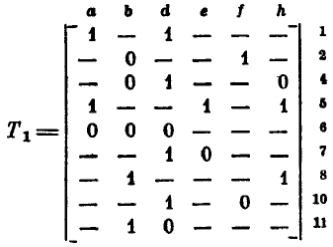
Обратив внимание на строку 6, мы видим, что она совместима только со строкой 2. Сливая эти строки, мы получаем каплю, уже не совместимую ни с чем и поэтому «вы падающую в осадок», т. е. вводимую в матрицу U, где накапливаются элементы решения (вначале эта матрица пустая):
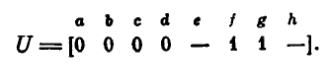
Напомним, что в столбцах с и g мы договорились ставить соответственно 0 и 1.
После удаления из матрицы Т строк 2 и 6 столбец а оказывается без нулей и поэтому тоже удаляется с соответствующими оговорками. Аналогичная операция выполняется над столбцом f. После этого устанавливается отношение импликации между сроками 4 и 1, а также между строками 7 и 10. Имплицируемые строки 1 и 10 удаляются, и матрица Т сокращается до
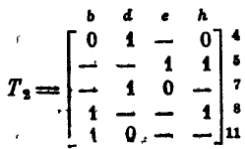
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.