Поиск приближений. Найти оптимальное решение удается далеко не всегда, так как для большинства практических задач на это потребовалось бы слишком много времени. В связи с этим широкое распространение получили разнообразные методы нахождения «достаточно хороших» приближений к оптимальным методам, или, как мы будем называть их ради краткости, приближенные методы.
Производимый в приближенных методах перебор вариантов существенно сокращается путем отбрасывания менее перспективных из них. Однако делается это без гарантии того, что среди отбрасываемых вариантов не окажется оптимальный. Сокращение перебора оправдывается лишь статистически.
Допустим, что все концевые вершины дерева поиска представляют собой решения, хотя по качеству они могут сильно различаться.
Для отсечения менее перспективных вариантов можно ввести некоторый порог, считая, что если для некоторой ситуации значение оценки стоимости превышает порог, то ситуация бракуется и не расщепляется. Очевидно, что при этом порог не должен быть ниже минимальной среди оценок рассматриваемых ситуаций. Порог может фиксироваться на все время решения задачи (например, если известна заранее стоимость оптимального решения), а может и изменяться в процессе поиска. Изменяя значение порога, можно регулировать время, затрачиваемое на поиск решения. Понижение порога будет приводить к уменьшению этого времени, однако следует помнить, что при этом может пострадать качество находимого решения.
Планирование времени осуществляется легче, если оценки стоимости используются не для сравнения с порогом, а лишь для линейного упорядочения конкурирующих между собой ситуаций, с целью последующего выбора некоторого заданного числа тех из них, которые оказались наиболее перспективными. Рассмотрим некоторые варианты такого подхода, которые можно использовать для соответствующих модификаций метода обхода и метода поярусного построения дерева поиска.
Один из этих вариантов заключается в ограничении коэффициента ветвления рассматриваемых ситуаций задаваемым заранее числом k. При этом, после расщепления каждой из рассматриваемых ситуаций, из продуктов расщепления выбираются для последующего рассмотрения ровно k ситуаций (или вес продукты расщепления, если
|
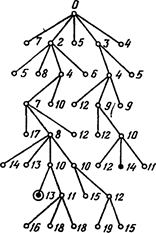
Рис. 32. Поиск решения методом невода при k = 2. |
|
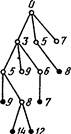
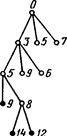
Рис. 31. Обход дерева поиска с ограничением на коэффициент ветвления: а) при k = 1 находится решение стоимостью 9; б) при k = 2 находится решение стоимостью 7. |
их число меньше k). Например, положив значение k равным единице, мы получим самый быстродействующий и в то же время наиболее грубый способ поиска решения.
На рис.31 показан результат применения данной модификации метода обхода дерева поиска к старому примеру (см. рис. 28). Заметим, что если какое-то решение уже найдено, но оценка стоимости в некоторой из еще не расщепленных ситуаций ниже стоимости полученного решения, то поиск лучшего решения будет продолжаться даже при k = 1.
При достаточно большом числе ярусов количество рассматриваемых ситуаций может сильно разрастись, если k > 2. В этом случае для гарантированного сокращения объема вычислений удобнее ограничить не коэффициент ветвления отдельных ситуаций, а коэффициент ветвления яруса в целом. Эта идея может быть использована для модификации метода поярусного построения дерева поиска и реализуется путем выбора на каждом ярусе k наиболее перспективных ситуаций или всех ситуаций данного яруса, если их число меньше k (рис. 32). Назовем данный способ поиска решения методом невода.
Метод невода особенно удобен, когда сильно ограничивается память для запоминания промежуточных результатов поиска. Действительно, продвигаясь от предшествующего яруса к последующему, достаточно фиксировать каждый раз информацию о k ситуациях.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.