Одно- и многоразрядные алгебраические сумматоры

Одно- и многоразрядные алгебраические сумматоры

Под алгебраическим суммированием понимается суммирование чисел с произвольными знаками, т.е. положительных и отрицательных. Знак положительного числа в двоичном коде принято отображать нулем (отсутствием заема), отрицательного - единицей (наличием заема), стоящими в специальном знаковом разряде, расположенном левее самого старшего значащего разряда, т.е. там, где обычно ставится плюс или минус.

Алгебраическое суммирование чаще всего производится переводом отрицательных чисел из прямого (натурального) двоичного кода в дополнительный код, что позволяет использовать при этом в качестве основного элемента арифметический сумматор.

Если в прямом коде используется m-разрядное двоичное отрицательное число Апр, то в дополнительном коде это число можно выразить следующим образом:

Адоп = 2m - Апр.

Число 2mкак раз и является тем самым заемом, который обычно используется при вычитании и соответствует единице в (m + l)-м(знаковом) разряде.

Например, число минус шесть (-6) в натуральном двоичном (прямом) коде записывается как 1.110, т.е. одна единица в знаковом разряде означает минус, а три значащих разряда (m = 3) соответствуют шести. Применяя формулу

Адоп = 2m - Апр, находим 23 - 6 = 2, откуда в дополнительном коде число -6 запишем как Адоп = 1.010.

Число значащих разрядов следует выбирать так, чтобы сумма чисел по абсолютному значению не превосходила 2m - 1. Если при этом условии в результате сложения образуется перенос в область знакового разряда, то и там используется суммирование по модулю два.

Например, 5 - 3 = 2 в дополнительном коде будет выглядеть следующим образом: 0.101 + 1.101 =0.010. Единица (заем) в знаковом разряде второго слагаемого, соответствующая числу 2m,здесь компенсировалась единицей переноса из старшего значащего разряда суммы.

Правило формирования дополнительного кода содержит процедуру вычитания, которую необходимо заменить сложением. Для этого используется возможность перехода от натурального двоичного (прямого) кода к дополнительному через так называемый обратныйкод, все значащие разряды которого являются инверсными (обратными) по отношению к одноименным разрядам прямого кода (табл. 2.2).

Таблица 2.2

Таблица истинности прямого, дополнительного и обратного кодов

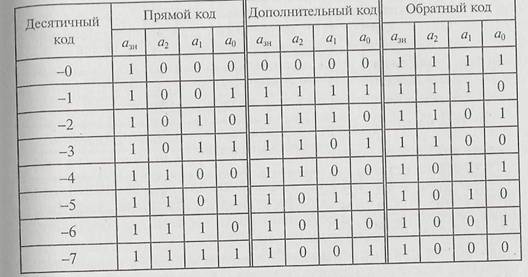
Действительно, обратный код определяется формулой

Аобр = (2m – 1) - Апр.

Каждый канал контроллера прямого доступа к памяти состоит из следующих 16-разрядных регистров (см. рис. 2.6): регистр текущего адреса (CAR), регистр циклов прямого доступа к памяти (CWR), регистр хранения базового адреса (BAR), регистр хранения базового числа циклов прямого доступа к памяти (WCR) и 6-разрядного регистра режима (MR).

В двоичном коде число (2m – 1) выражается с помощью m единиц, стоящих в значащих разрядах, поэтому, если из него вычесть любое m-разрядное число Апр в двоичном коде, то в тех разрядах Апр, где стояли единицы, в результате появятся нули, а где стояли нули, останутся единицы. Тем самым мы доказали, что при выполнении равенства

Аобр = (2m – 1) - Апр значащие разряды числа Апр подвергаются инверсии, откуда и название «обратный код».

Сравнивая Апр и Аобр, находим, что

Адоп = Аобр + 1.

Следовательно, применяя инвертирование значащих разрядов прямого кода и последующее суммирование с единицей, можно получить дополнительный код без операции вычитания. Учитывая, что инвертирование разрядов необходимо производить только при наличии единицы в знаковом разряде, его можно реализовать с помощью элементов Исключающее ИЛИ. Тогда весь преобразователь числа из прямого кода в дополнительный содержит m элементов Исключающее ИЛИ, преобразующих число в обратный код, и сумматор числа в обратном коде со значением знакового разряда (в случае отрицательного числа - с единицей) (рис. 2.13).

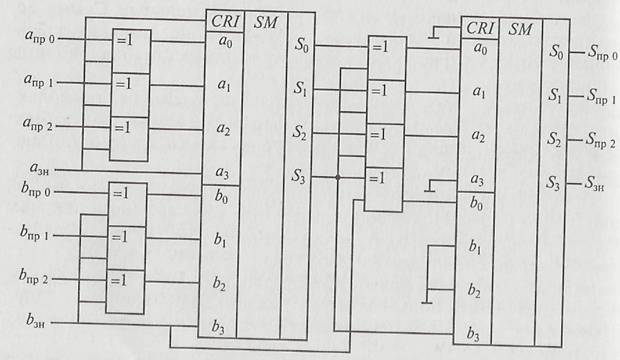
Рис. 2.13. Схема преобразователя двоичного прямого кода в дополнительный

Поскольку в результате алгебраического суммирования на выходе число получается в дополнительном коде (в случае отрицательного значения суммы), необходимо осуществлять обратное преобразование дополнительного кода в прямой. Однако для этого не надо изобретать новый преобразователь, поскольку прямой и дополнительный коды являются взаимно дополняющими. Действительно, если поменять местами кодовые значения (см. рис. 2.13), т.е. записать