Апр = 2m - Адоп и подставить в эту формулу выражение для Адоп, получим тождество Апр = Апр. Теперь очевидно, что после алгебраического суммирования необходимо использовать преобразователь, схема которого изображена на рис. 2.13.
Обобщая сказанное, приходим к выводу, что алгебраический сумматор должен содержать помимо основного (арифметического) сумматора еще три преобразователя кода (два до сумматора и один - после), включающие в себя элементы Исключающее ИЛИ и сумматоры.
От одного сумматора обратного кода со знаковым разрядом можно избавиться подачей этого знакового разряда (например, числа а) на вход переноса (CRI) основного сумматора (рис. 2.14). От другого такого же сумматора можно освободиться, используя возможность компенсации недостатка единицы в дополнительном коде второго слагаемого недостатком единицы в прямом коде алгебраической суммы.
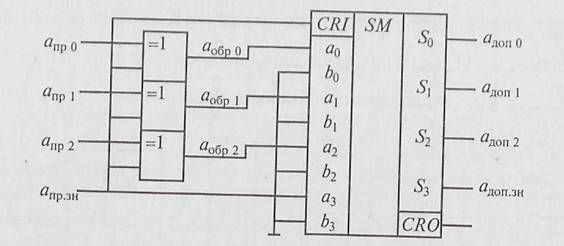
Рис. 2.14. Схема алгебраического комбинационного сумматора
Рассмотрим все возможные варианты, возникающие при такой методике синтеза (рис. 2.15).
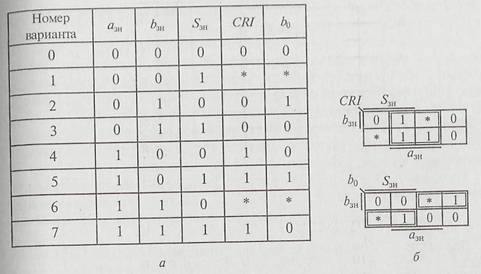
Рис. 2.15. Таблица истинности (а) и диаграммы Вейча (б) для определения функций добавления единиц в предварительный и выходной сумматоры, показанные на рис.2.14
В столбец CRI таблицы на рис. 2.15, а заносим информацию о сигналах, подаваемых на вход переноса основного сумматора; в столбец b0 - то, что необходимо внести в младший разряд выходного сумматора, входящего в состав преобразователя алгебраической суммы из дополнительного кода в прямой.
Начальный вариант. Оба слагаемых положительные. Сумма, естественно, тоже положительная. Следовательно, никаких добавлений единиц не требуется (в соответствующих столбцах таблицы ставим нули).
Вариант 1. Этот вариант является запрещенным, поскольку невозможно, чтобы при положительных слагаемых сумма была отрицательной. Следовательно, в столбцах выходных функций таблицы ставим значок факультатива (*).
Вариант 2. Например: А = 6; В = -2; S = 4. В прямом коде А = 0.110; В = 1.010. В обратном коде В = 1.101. При суммировании получим 0.110 + 1.101 = 0.011, что на единицу меньше требуемого. Следовательно, на выходе необходимо добавить единицу (b0 = 1).
Вариант 3. Сделаем так, чтобы вычитаемое стало больше уменьшаемого и разность получилась отрицательной. Например: А = 2; В = -6. В прямом коде A = 0.010; B = 1.110. В обрат-ном коде В = 1.001. При суммировании получим 0.010 + 1.001 = 1.011. Перевод в обратный код путем инвертирования значащих разрядов дает значение 1.100, соответствующее истинной алгебраической сумме в прямом коде (-4). Следовательно, добавления единицы в выходной сумматор не требуется (b0 = 0).
Вариант 4. Здесь не требуется рассматривать конкретные примеры, поскольку только одно слагаемое является отрицательным, и добавление единицы осуществляется в основном сумматоре (СRI = 1). Так как сумма при этом является положительной, на выходе в добавлении единицы нет необходимости.
Вариант 5. Поскольку на входе аккуратно оформляется число А в дополнительном коде, на выходе также требуется добавление единицы к сумме, выраженной в обратном коде.
Вариант 6. Этот вариант является запрещенным, поскольку два отрицательных числа не могут в сумме давать положительное число. Отсюда следует факультативность сигналов на входах основного и выходного сумматоров.
Вариант 7. Возьмем в качестве примера А = -3; В = -2. Сумма чисел А в дополнительном коде (А = 1.101) и В в обратном коде (В = 1.101) соответствует выражению 1.010, переводя которое в обратный код, получим 1.101, что соответствует в прямом коде значению минус пять. Следовательно, в этом варианте добавлять единицу в выходной сумматор не нужно.
Занесем данные таблицы истинности, приведенной на рис. 2.15, а, в диаграммы Вейча на рис. 2.15, б. После объединения единиц и факультативов в контуры получим следующие уравнения:
![]()
Эти уравнения и реализованы в схеме на рис. 2.14.
Иногда возникает необходимость суммировать множество единиц с разными знаками. В этих случаях можно использовать алгебраические одноразрядные мультисумматоры. В качестве примера на рис. 2.16 приведен семивходовой алгебраический мультисумматор.
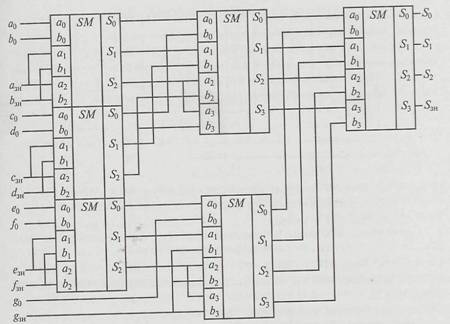
Рис. 2.16. Схема семивходового алгебраического комбинационного сумматора
Из представленной схемы видно, что основу устройства составляют трех- и четырехразрядные комбинационные сумматоры. Алгебраическая сумма единиц на выходе сумматора представлена в дополнительном коде.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.