Синтез цифровых схем арифметических устройств (исходные операнды - десятичные числа: Мн = 18,04, Мт = 6,77; алгоритм выполнения операции умножения: Б)

Мультиплексор – это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие n = 2^m.На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на информационные входы. Порядковый номер информационного входа, значение с которого в данный момент должно быть передано на выход, определяется двоичным кодом на управляющих входах.

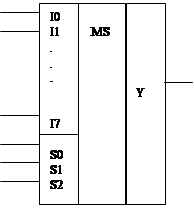
Для синтеза ОЧС будем использовать мультиплексор  “один из восьми” (1 из 8-ми).

Входы I₀,I₁,…, I₇ - это информационные входы мультиплексора. Сигналы х₁ могут принимать значения 0 или 1.

Входы S₀ ,S₁ , S₂ - управляющие входы.

 

Используя таблицу истинности ОЧС , составим таблицу истинности для построения ОЧС на мультиплексорах .

A1	A2	B1	P1	S1	S2
0	0	0	1	B2 P+ B2 P + B2 P= B2 P+ P	B2 P+ B2 P
0	0	1	B2 P+ B2 P +B2 P = B2 P + B2	B2 P+ B2 P	B2 P
0	1	0	B2 P+ B2 P= B2	B2 P +B2 P+ B2 P= B2 P+ B2	B2 P+ B2 P
0	1	1	B2 P	B2 P	B2 P+ B2 P+ B2 P= B2 P+ B2
1	0	0	B2 P	B2 P+ B2 P=P	B2 P+ B2 P= B2
1	0	1	0	B2 P+ B2 P = P	B2 P+ B2 P
1	1	0	B2 P +B2 P +B2 P= B2 P+P	B2 P+ B2 P=P	B2 P+ B2 P= B2
1	1	1	B2 P+ B2 P =  B2	B2 P +B2 P= P	B2 P+ B2 P

Управление мультиплексором осуществляется тремя переменными: A₁,A₂,B₁ ,а вход соответствующих значений функций на информационные входы обеспечивается реализацией этих функций на дополнительных логических элементах.

5.1.4 Функциональная схема ОЧС на мультиплексорах:

a1 a2 b1 b2     p

 

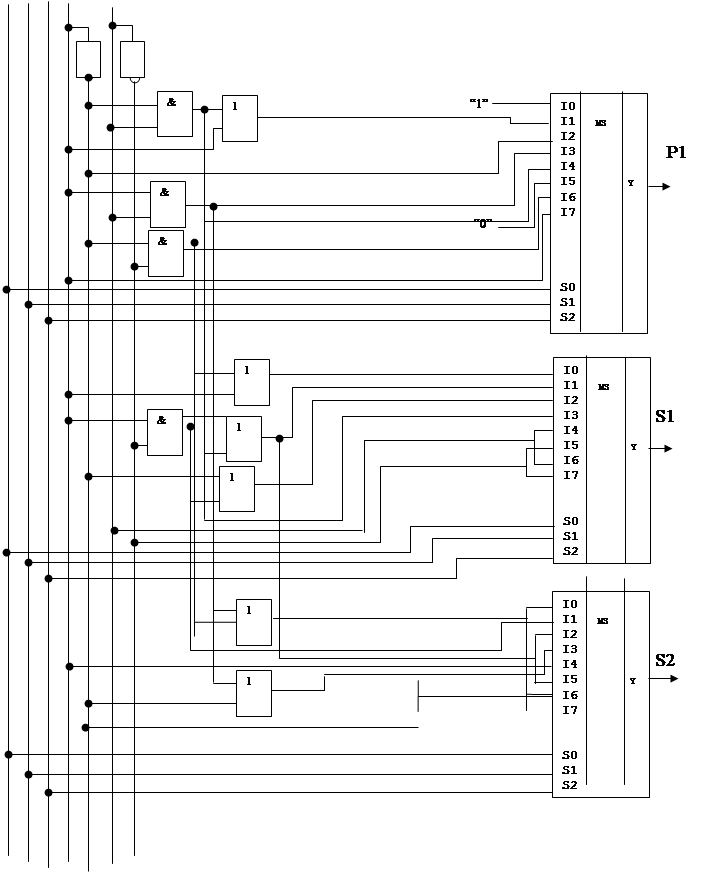
5.2 ЛОГИЧЕСКИЙ СИНТЕЗ

ОДНОРАЗРЯДНОГО  ЧЕТВЕРИЧНОГО  УМНОЖИТЕЛЯ-СУММАТОРА

ОЧУС - это комбинационное устройство, имеющее 6 входов (2 разряда из регистра МН, 2 разряда из регистра Мт, вход переноса и управляющий вход h) и 3 выхода. Принцип работы ОЧУС описывается с помощью таблицы истинности (табл.4).

Разряды множителя закодированы : 0 - 00; 1 - 01; 2 - 10; 3 - 11.

Разряды множимого закодированы : 0 - 10; 1 - 01; 2 - 11; 3 - 00.

Управляющий вход h определяет тип операции: 0 - умножение закодированных цифр, поступивших на информационные входы, и добавление переноса; 1 - вывод на выходы без изменения значения разрядов, поступивших из регистра множимого.

Табл. 4

Пер.	Мн		Мт		Упр.		Перенос	Результат		Результат операции
Р1	Х1	Х2	У1	У2	h		Р	Q1	Q2	В четверичной с/с
0	0	0	0	0	0		0	1	0	3*0+0=00
0	0	0	0	0	1		0	0	0	Выход - код «03»
0	0	0	0	1	0		0	0	0	3*1+0=02
0	0	0	0	1	1		0	0	0	Выход – код «03»
0	0	0	1	0	0		1	1	1	3*2+0=12
0	0	0	1	0	1		0	0	0	Выход - код «03»
0	0	0	1	1	0		X	X	X	3*3+0=21	*
0	0	0	1	1	1		X	X	X	Выход – код «03»	*
0	0	1	0	0	0		0	1	0	1*0+0=00
0	0	1	0	0	1		0	0	1	Выход – код «01»
0	0	1	0	1	0		0	0	1	1*1+0=01
0	0	1	0	1	1		0	0	1	Выход – код «01»
0	0	1	1	0	0		0	1	1	1*2+0=02
0	0	1	1	0	1		0	0	1	Выход - код «01»
0	0	1	1	1	0		X	X	X	1*3+0=03	*
0	0	1	1	1	1		X	X	X	Выход – код «01»	*
0	1	0	0	0	0		0	1	0	0*0+0=00
0	1	0	0	0	1		0	1	0	Выход – код «00»
0	1	0	0	1	0		0	1	0	0*1+0=00
0	1	0	0	1	1		0	1	0	Выход – код «00»
0	1	0	1	0	0		0	1	0	0*2+0=00
0	1	0	1	0	1		0	1	0	Выход - код «00»
0	1	0	1	1	0		X	X	X	0*3+0=00	*
0	1	0	1	1	1		X	X	X	Выход – код «00»	*
0	1	1	0	0	0		0	1	0	2*0+0=00
0	1	1	0	0	1		0	1	1	Выход – код «02»
0	1	1	0	1	0		0	1	1	2*1+0=02
0	1	1	0	1	1		0	1	1	Выход – код «02»
0	1	1	1	0	0		1	1	0	2*2+0=10
0	1	1	1	0	1		0	1	1	Выход - код «02»
0	1	1	1	1	0		Х	Х	Х	2*3+0=12	*
0	1	1	1	1	1		X	X	X	Выход – код «02»	*
1	0	0	0	0	0		X	X	X	3*0+1=01	*
1	0	0	0	0	1		X	X	X	Выход – код «03»	*
1	0	0	0	1	0		X	X	X	3*1+1=10	*
1	0	0	0	1	1		X	X	X	Выход – код «03»	*
1	0	0	1	0	0		1	0	0	3*2+1=13
1	0	0	1	0	1		X	X	X	Выход - код «03»	*
1	0	0	1	1	0		X	X	X	3*3+1=22	*
1	0	0	1	1	1		X	X	X	Выход – код «03»	*
1	0	1	0	0	0		X	X	X	1*0+1=01	*
1	0	1	0	0	1		X	X	X	Выход – код «01»	*
1	0	1	0	1	0		X	X	X	1*1+1=02	*
1	0	1	0	1	1		X	X	X	Выход – код «01»	*
1	0	1	1	0	0		0	0	0	1*2+1=03
1	0	1	1	0	1		X	X	X	Выход – код «01»	*
1	0	1	1	1	0		X	X	X	1*3+1=10	*
1	0	1	1	1	1		X	X	X	Выход – код «01»	*
1	1	0	0	0	0		X	X	X	0*0+1=01	*
1	1	0	0	0	1		X	X	X	Выход – код «00»	*
1	1	0	0	1	0		X	X	X	0*1+1=01	*
1	1	0	0	1	1		X	X	X	Выход – код «00»	*
1	1	0	1	0	0		0	0	1	0*2+1=01
1	1	0	1	0	1		X	X	X	Выход – код «00»	*
1	1	0	1	1	0		X	X	X	0*3+1=01	*
1	1	0	1	1	1		X	X	X	Выход – код «00»	*
1	1	1	0	0	0		X	X	X	2*0+1=01	*
1	1	1	0	0	1		X	X	X	Выход – код «02»	*
1	1	1	0	1	0		X	X	X	2*1+1=03	*
1	1	1	0	1	1		X	X	X	Выход – код «02»	*
1	1	1	1	0	0		1	0	1	2*2+1=11
1	1	1	1	0	1		X	X	X	Выход – код «02»	*
1	1	1	1	1	0		X	X	X	2*3+1=13	*
1	1	1	1	1	1		X	X	X	Выход – код «02»	*

В таблице выделено 36 безразличных наборов, т.к. на входы ОЧУС из разрядов множителя не может поступить код 11, при умножении на 1(01) и на 0(10) не может возникнуть перенос.

Минимизируем функции  и P,Q1 и Q2 картами Карно-Вейча :

P:

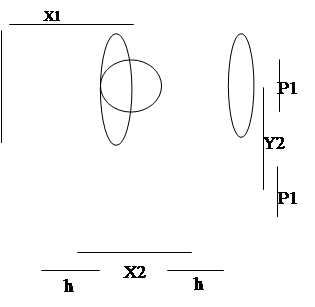			1				1
		*	1	1	*	*	*
*	*	*	*	*	*	*	*
*	*	*	*	*	*	*	*
*	*	*	*	*	*	*	*
*	*	*	*	*	*	*	*

	Y1

 

Pmin=y1h+y1x2p1h

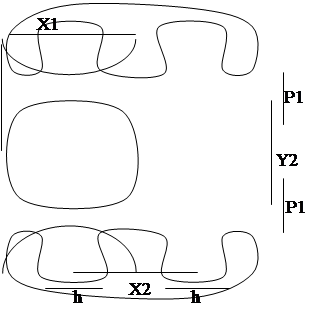
Q1:

1	1	1	1	1			1
		*			*	*	*
*	*	*	*	*	*	*	*
*	*	*	*	*	*	*	*
1	1	1	1
*	*	*	*	*	*	*	*
*	*	*	*	*	*	*	*
1	1	1	1	1			1

	Y1

Q1min=x1y2+x1x2h+y2hp1 +x1y2p1

Q2:

 

		1		1	1	1
1		*	1		*	*	*
*	*	*	*	*	*	*	*
*	*	*	*	*	*	*	*
		1	1		1	1
*	*	*	*	*	*	*	*
*	*	*	*	*	*	*	*
		1			1

 

Q2min=x2h+x1x2y2+x1y2h+ x1y1h+x1x2y1y2p1+x1x2y1p1+ x2y1p1h

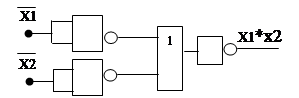
Для  построения схемы операцию *(и) представим как:

 

x1	x2	x1+x2	x1+x2=x1*x2
0 1 0 1	0 0 1 1	0 1 1 1	1 0 0 0

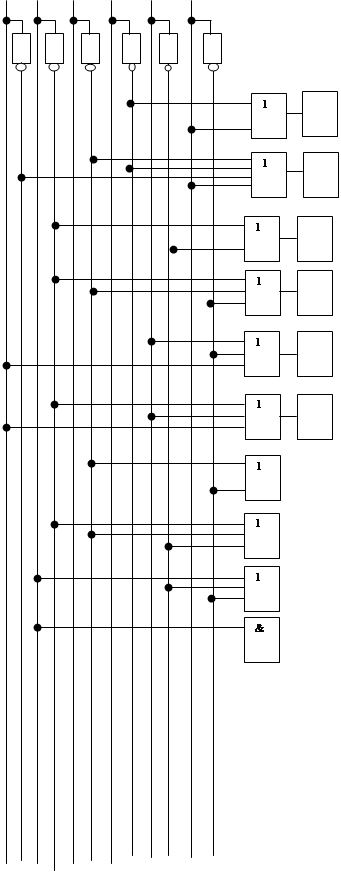
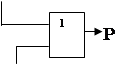
5.2.2 Функциональная схема ОЧУС в заданном базисе.

&

&

&

&

&

&

 

5.3. Логический синтез преобразователя множителя (ПМ)

Преобразователь множителя (ПМ) служит для исключения из множителя диад 11, заменяя их на триады 101.

 

Схематическое изображение ПМ.

        Таблица 5.13. Таблица истинности ПМ.

Входы ПМ				Выходы ПМ
Qn-1	Qn	P1		P2	S1	S2	M
0	0	0		0	0	0	0
0	0	1		0	0	1	0
0	1	0		0	0	1	0
0	1	1		0	1	0	0
1	0	0		0	1	0	0
1	0	1		1	0	1	1
1	1	0		1	0	1	1
1	1	1		1	0	0	0

После некоторых преобразований получим:

P = Q_n-1Q_nP₁ + Q_n-1Q_nP₁ + Q_n-1Q_nP₁₌ Q_n-1P₁ + Q_n-1Q_nP₁

S₁ = Q_n-1Q_nP₁+ Q_n-1Q_nP₁

S₂ = Q_n-1Q_nP₁+ Q_n-1Q_nP₁ + Q_n-1Q_nP₁ + Q_n-1Q_nP_{1 =} Q_nP₁ + Q_nP₁

M= Q_n-1Q_nP₁ + Q_n-1Q_nP₁

 

 

 

 

 

 

 

 

5.3.1 Функциональная схема преобразователя множителя :

Q_n-1  Q_n   P₁

 

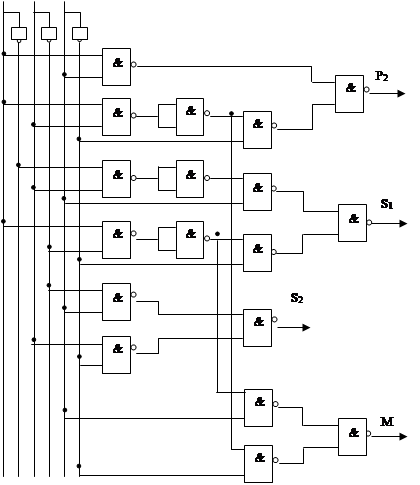Рис.Функциональная схема преобразователя множителя.

5.1.1 Оценка эффективности минимизации переключательных функций

Для проведения оценки эффективности минимизации переключательных функций необходимо посчитать

цену схемы до минимизации и цену схемы, которая будет построена на элементах заданного базиса и синтезированных элементах И, ИЛИ, НЕ. Сравнить их и  просчитать эффективности минимизации , которая определяется как:

 

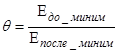
Все рассчитанные данные сведены в таблицу.

Цену каждой отдельной схемы, построенной по данным выражениям можно посчитать как:

C (ОЧС) =I+Nili*6+Mne*2+B*2

Nili— число синтезированных элементов ИЛИ, используемых в схеме. с = 6(входов).

Mne—  число синтезированных элементов НЕ, используемых в схеме. с = 2.

B—  число элементов заданного базиса, используемых в схеме. с = 2.

I— сумма чисел входов каждого элемента И, используемого в схеме.

Преобразование к заданному базису полученных переключательных функций в результате минимизации алгоритмом Рота приведет к снижению цены схемы, а значит минимизация станет еще более эффективнее.

До минимизации алгоритмом Рота:

C(p)=16*5i+15*6ili+5*2ne=181

C(S1)=17*5i+16*6ili+5*2ne=191

C(S2)=16*5i+15*6ili+5*2ne=181

После минимизации алгоритмом Рота:

P1min=a1a1b1b2+a1a2p+b1b2p+a1a2b2+a1b1b2+a1a2b1

C1(p)=(4+5*3)i+5*6ili+9*2ne=67

S1min=a1b1b2 p+ a1b1p  +a1b1p+ a1b1p + a1 a2 b2p

C1(S1)=(4*2+3*3)i+4*6ili+9*2ne=59

S2min=a2b1 b2p+a2b1b2p+ a2b1b2 p  +a1a2b1b2p +a1a2 b1b2p +a1a2b1b2p+a1a2b2p.

С1(S2)=(4*4+5*2)i+6*6ili+16*2ne=70

После привидения к заданному базису:

P=a1a2pb2b1+a2b2(b1p+a1b1)

C2(p)=(5+2+2+3)i+2*6ili+5*2ne=34

S1=a1b1(b2pa2+p)+a1(b1Å p)

C2(S1)=(3+3+2)i+2*6ili+1*2b+5*2ne=32

S2=a2(b2(b1Åp)+a1(b1+(b2Åp))+a1b1b2 p)+a2b2(b1+a1b1p)

C2(S2)=(2+2+4+2+3+3)i+2*2b+5*6ili+8*2ne

q1=C(f)/C1(f); q2=C1(f)/C2(f)

Цена всей схемы будет равна сумме цен трех выходов схемы :

                               Csum=C(fp)+C(fs1)+C(fs2)=181+191+181=553

                               C1sum=C1(fp)+C1(fs1)+C1(fs2)=67+59+70=196

                               C2sum=C2(fp)+C2(fs1)+C2(fs2)=34+32+66=132

Выходы схемы	Рассчитанная цена схемы
	До минимизации алгоритмом Рота		После минимизации		После приведение к заданному базису
	181	2.7	67	1.97	34
	191	3.2	59	1.84	32
	181	2.58	70	1.06	66
вся схема	553	2.82	196	1.48	132

5.2.1 Оценка эффективности минимизации переключательных функций

Аналогично пункту 3.1.3, для проведения оценки эффективности минимизации переключательных функций необходимо посчитать цену схемы до минимизации и цену схемы, которая будет построена на элементах заданного базиса и синтезированных элементах И, ИЛИ, НЕ. Цену каждой отдельной схемы, построенной по данным выражениям можно посчитать как:

C(ОЧУС)=Ni*(n+1)+Mili.

Ni—число синтезированных элементов и в схеме, где n+1—число входов,

Mili—число входов элементов или в схеме.

Преобразование к заданному базису полученных переключательных функций в результате минимизации картами вейча приведет к снижению цены схемы, а значит минимизация станет еще более эффективнее.

До минимизации картами Вейча:

P=p1x1x2y1y2h +p1x1x2y1y2h +p1x1x2y1y2h+ p1x1x2y1y2h

С(p)=4*7i+4ili=32

Q1= p1x1x2y1y2h+ p1x1x2y1y2h +p1x1x2y1y2h +p1x1x2y1y2h +p1x1x2y1y2h+